Физика ХХI века:
классический ренессанс

К.П. Агафонов

Глава 1. Законы классической механики

На базе фундаментальных характеристик
деформирования реальных тел: вязкости,
упругости и пластичности — предлагается
универсальная модель физических
взаимодействий, описывающая как механику
сплошной среды, так и движение отдельной
материальной частицы.

1.1. Историческая справка

Первым удачным примером объединения физических явлений: электрических, магнитных, оптических — принято считать уравнения электродинамики Максвелла. Они были получены с помощью механической аналогии электромагнитных явлений, в основе которой лежало следующее глубокое убеждение автора: «Говоря об энергии поля, я хочу быть понятым буквально. Всякая энергия есть то же, что и механическая энергия, существует ли она в форме обычного движения, или в форме упругости, или в какой-нибудь другой форме. Энергия электромагнитных явлений — это механическая энергия. Единственный вопрос заключается в том, где она находится» [11].

Дюгем, известный в прошлом историк физики, назвал механическую модель (довольно сложную) в теории Максвелла «паразитирующим растением на крепком и полном жизни дереве». Однако подавляющее большинство физиков ХIХ века: Клаузиус, В. Томсон, Гельмгольц, Больцман, Герц, Лоренц — глубоко верили в возможность механического объяснения немеханических явлений (вспомним слова В. Томсона: «объяснить — это значит построить механическую модель») . Эта вера ещё более утвердилась с широким распространением вариационных принципов механики на описание немеханических явлений и достигла апогея в период создания кинетической теории газа (модель Крёнига) и выявления микроструктуры вещества (модель атома Бора). Затем механические модели в физике уступили место формальным релятивистским и квантовым представлениям.

Однако многие выдающиеся исследователи эпохи становления современной физики, включая Планка, Лауэ, Шредингера и других, были категорически против радикального изменения физического мировоззрения. «Классическая теория дала нам столько полезного, — предостерегал Планк в письме к А. Ф. Иоффе, — что к ней надо относиться с величайшей осторожностью и охранять её». А выдающийся русский учёный и педагог Н. Е. Жуковский прямо призывал: «Математическая истина только тогда должна считаться вполне обработанной, когда она может быть объяснена всякому из публики, желающему её усвоить». Такую задачу и выполняет моделирование, которое он определил как «высшую степень наглядности» [12].

1.2. Вязкость, упругость и пластичность

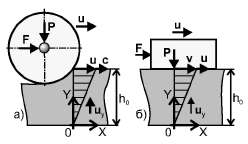
Для построения исходной расчётной модели взаимодействия реальных физических тел в простейшем одномерном случае обратимся к рис. 1.1. Здесь на примере движения элементов реального устройства — опорного колеса (а) и полевой доски (б) плуга — представлены два вида трения, связанные с двумя видами деформирования среды. Трение качения ( рис. 1.1, а) обусловлено уплотнением (сжатием) грунта, в результате чего частицы его перемещаются в направлении нормали к поверхности колеса со скоростью, горизонтальная составляющая которой равна скорости u движения колеса.

Рис. 1.1.
Схема «течения» граничного слоя при качении (а) и
скольжении (б) тел по деформируемой опоре грунту)

Трение скольжения (рис. 1.1, б) сопровождается сдвигом частиц грунта со скоростью v, меньшей скорости u тела. Напряжения сжатия и сдвига грунта определяются по величине потребной толкающей силы F, отнесенной к характерной площади s деформатора. Перемещение частиц грунта распространяется на некоторую конечную глубину h₀. называемую граничным или контактным слоем. Изменение скорости частиц по высоте слоя показано на рисунке заштрихованными фигурами и в первом приближении может быть принято линейным.

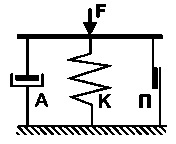
Задача состоит в том, чтобы описать процессы трения на базе известных фундаментальных законов деформирования тел, в частности, грунта при сжатии и сдвиге: закона Гука, характеризующего упругое поведение твёрдых тел в пределах малых величин деформаций; и закона Ньютона, описывающего вязкое течение реальных жидкостей. Так как в любых реальных телах оба эти свойства — упругость и вязкость — в большей или меньшей мере проявляются совместно, то для этого в расчётную модель трения (рис. 1.2) помимо фрикционного элемента, характеризующего «чистое» или идеальное внешнее трение (сила П), обусловленное вертикальной нагрузкой P (см. рис. 1.1) на контакте, необходимо ввести также упругий (пружинный) K и вязкий (гидравлический демпфирующий) A элементы и определять силу трения как алгебраическую сумму трёх составляющих.

Рис. 1.2.
Вязкоупругопластическая модель
деформирования реальных тел

Такая модель называется вязкоупругопластической, поскольку элемент трения характеризует осо бый вид деформирования тел — пластическое течение, при котором сила сопротивления сохраняет постоянную величину.

Термин «упругость» здесь не следует понимать буквально, поскольку деформации большинства реальных тел полностью не восстанавливаются и не являются упругими в строгом смысле этого слова. В механике сплошных или деформируемых сред, в частности, в механике грунта этот термин широко используется для описания закона линейной деформируемости (квазиупругости) реальных тел в пределах ограниченных величин деформаций.

Закон Гука для твёрдых тел определяет пропорциональность квазиупругих сил относительному изменению объёма тел или относительной их деформации; коэффициент пропорциональности K, называемый модулем упругости или жёсткостью, характеризует напряжённость деформируемого тела. Закон Ньютона для реальных жидкостей определяет пропорциональность вязких сил градиенту скорости частиц в граничном слое; коэффициент пропорциональности A называют коэффициентом вязкости ньютоновской жидкости. Примем далее во внимание, что абсолютная величина объёмной деформации ΔV грунта за малый промежуток времени Δt, задающий малую величину относительной деформации, пропорциональна скорости u деформирования ΔV = suΔt; а полный объём V грунта, вовлекаемого в процесс деформирования за то же время, — скорости с распространения деформаций в среде V = scΔt. Тогда величина относительной деформации грунта при качении колеса определится как отношение указанных скоростей:

ΔV/V = β = u/c ≤ 1,0.

Для скользящего тела полный объём V грунта, подвергаемого сдвигу за малый промежуток времени, пропорционален скорости u скольжения, а абсолютная величина объёмной деформации ΔV — скорости v частиц грунта. Поэтому относительную деформацию сдвига можно определить соотношением:

ΔV/V = γ = v/u ≤ 1,0.       (1.1)

Таким образом, вязкоупругопластическая или AKП-модель по рис. 1.2 позволяет составить следующие два интегральных уравнения деформирования тел — при сжатии и сдвиге соответственно:

F = П + Kβ – Adu/dy,       (1.2а)

F = П + Kγ – Adv/dy.       (1.2б)

В них знак минус перед последним слагаемым учитывает разгружающее свойство текущего граничного слоя, обусловленное одинаковым направлением действия внешней силы F и вязкой составляющей силы сопротивления движению (см. рис. 1.1).

С учётом соотношения (1.1) для случая линейного распределения скоростей частиц в граничном слое: du/dy ≈ u/h₀ ,  dv/dy ≈ v/h₀ — получим приближённую форму уравнений деформирования:

F ≈ П + Kβ – au,       (1.3)

F ≈ П + Kγ – aγu,       (1.4)

a = A/h₀         (1.5)

a — коэффициент объёмной вязкости или просто вязкость граничного слоя. Для констант A, К и П в обоих случаях здесь приняты одинаковые обозначения, но необходимо иметь в виду, что характеризуют они разные процессы и по величине могут быть различными.

1.3. Уравнение движения частицы

Полученные уравнения пригодны для решения задач механики сплошных или деформируемых сред, которая оперирует с системой бесконечного числа материальных частиц. Чтобы перейти к механике отдельной частицы, вязкую составляющую силы трения представим в следующем виде:

A du/dy = (A dt/dy)(du/dt).

Здесь слева стоит сила, а величина du/dt характеризует ускорение тела. Коэффициент пропорциональности Adt/dy назовём инертной массой m вещества, подвергаемого деформированию или перемещению, полагая её для наглядности пропорциональной суммарной массе частиц граничного слоя:

m = A dt/dy ~ Σ_i m_i,

где m_i — инертная масса отдельной частицы слоя, [Σ_i — сумма по всем частицам]. Отсюда определяется физический смысл коэффициента кинематической вязкости:

A ~ Σ_i m_i dy/dt ~ Σ_i m_i u_y,

где u_y — поперечная (в направлении нормали к скорости основного движения) составляющая скорости частиц в граничном слое (см. рис. 1.1). Следовательно, природа вязких сил обусловлена наличием помимо продольного также и поперечного импульса частиц в граничном слое, вследствие чего быстро движущиеся частицы при переходе из одной части слоя в другую замедляются, а медленно движущиеся ускоряются. С учётом сказанного уравнение (1.2) представим в форме, пригодной для описания движения отдельной частицы в деформируемой среде:

F = П + Ku/c – m du/dt.       (1.6)

В общем случае упругие свойства среды или другого силового поля могут характеризоваться векторной величиной. Тогда, в частности, уравнения (1.2) и (1.6) предстанут в виде равенства нулю векторной суммы сил, воздействующих на поток частиц или выделенную частицу:

F + П + [u/c, K] + A du/dy = 0,       (1.7a)

F + П + [u/c, K] + m du/dt = 0.       (1.7б)

При этом необходимо строго отличать реальную внешнюю силу F от сил внутренних — пластической, упругой и вязкой составляющих реакции рассматриваемой системы на воздействие внешней силы, характеризующей физические свойства этой системы.

Слагаемое [u/c, K] в этих уравнениях задаёт упругую силу в направлении, перпендикулярном основному движению; она обуславливает закрутку потока или частицы при поступательном движении, повсеместно наблюдаемую в реальной жизни. В частных случаях эта сила проявляет себя либо как сила Кориолиса, если речь идёт о нейтральных частицах, либо как магнитная сила, если речь идёт о движении заряда. Полученные уравнения взаимодействия материальных тел и соответствующая им модель по рис. 1.2 используются далее для построения основных разделов физики.

1.4. Законы динамики Ньютона

Для нежёстких и слабо деформируемых систем без трения, определяемых условием [u/c, K] = 0 и П = 0, на основании уравнения (1.7) получаем:

F + m du/dt = 0       (1.8)

или F = – F_ин .       (1.9)

То есть имеем две силы, одна из которых — внешняя — возбуждает ускорение тела

F = m du/dt,       (1.10)

в то время как другая сопротивляется ему. Эту последнюю называют силой инерции и определяют соотношением

F_ин = – m du/dt,       (1.11)

где m — инертная масса тела. Её направление противоположно направлению вектора ускорения.

При F = 0 из уравнения (1.8) получаем два соотношения

m du/dt = 0;       u = const,

которые определяют частный случай движения свободного тела и утверждают так называемый принцип инерции или первый закон динамики Ньютона: если на тело не действуют внешние силы, то оно покоится или движется равномерно и прямолинейно. При этом из принципа фактически выпадают два практически важных случая движения по инерции: вращение и вращательно-поступательное движение.

Родоначальником принципа инерции справедливо принято считать Галилея. Однако последний, как уже было сказано, полагал, что движением по инерции является равномерное обращение тела по окружности; идея же о прямолинейном движении по инерции была выдвинута позднее, в частности, её придерживался Декарт. Ньютон в своём «Законе 1» к движению по инерции относил как равномерное и прямолинейное движение свободного тела, так и вращательное движение планет и комет в свободном пространстве [1]. И в нашем случае появляется неформальная возможность исправить ситуацию в следующей обобщённой формулировке принципа инерции Галилея: движение свободного тела в общем случае включает равномерное вращение и равномерное поступательное перемещение.

Из уравнения (1.7) при F = 0 и П = 0 для этого случая имеем:

[u/c, K] = – m du/dt.       (1.12)

Величина, стоящая справа, здесь, как и ранее, характеризует силу инерции, которая в случае вращающегося тела называется центробежной силой инерции; параметр слева характеризует ответную упругую реакцию материала вращающегося твёрдого тела, уравновешивающую указанную центробежную силу инерции.

Соотношение (1.10) подтверждает основной закон динамики или второй закон Ньютона, установленный экспериментальным путём и утверждающий: внешняя сила равна произведению массы тела на ускорение, которое она сообщает телу. Соотношение (1.9) составляет содержание третьего закона Ньютона и утверждает равенство внешнего действия и инерционного противодействия.

1.5. Силы инерции

Подчеркнём принципиально важное: возникновение сил инерции (1.11) и компенсирующих их сил упругости (1.12) есть объективное внутреннее свойство реальных тел, проявляемое при всяком воздействии на них внешней силы или вращающего момента в виде ответной реакции на такое воздействие. Этим наш подход отличается от традиционного, в котором проявление этих сил связывают с выбором неинерциальной системы отсчёта: «Центробежные силы, как и всякие силы инерции, существуют лишь в ускоренно движущихся (вращающихся) системах отсчёта и исчезают при переходе к инерциальным системам» [13]. В последнем случае силам инерции фактически отказывают в реальности, полагая их фиктивными силами, обусловленными ускорением системы отсчёта, в которой сила измеряется. Такая точка зрения расходится с практикой полезного использования сил инерции или борьбы с ними в реальных механизмах. В частности, разрушение быстро вращающегося диска турбины обусловлено именно реальностью возникающих в нём внутренних центробежных сил, и размещение такого диска в инерциальной или какой-либо другой системе отсчета от этих сил и разрушения диск не спасает.

А авторы другого современного учебника физики на основании реальности сил инерции утверждают возможность использования их для кардинального решения энергетической проблемы: «Для любой системы тел, находящейся в неинерциальной системе отсчёта, силы инерции являются внешними силами; следовательно, здесь нет замкнутых систем, и потому не выполняются законы сохранения» [14] (т. 1, с. 239). И в подтверждение «движущего» характера сил инерции приводят такой довод: «если при резком торможении вагона сила инерции бросит вас вперёд, то вы эту силу будете ощущать также реально, как и силу тяжести. Точно также космонавт очень реально чувствует силу инерции, прижимающую его к креслу при разгоне ракеты». При этом забывают, что на находящихся вне вагона или ракеты указанная сила никак не действует. Иными словами, сила инерции в этих и других подобных случаях проявляет себя исключительно как внутренняя сила системы вагон-пассажир или космонавт-ракета, но не как внешняя сила.

1.6. Обобщённый принцип инерции

Движение тел в реальном физическом пространстве осуществляется при наличии и под влиянием внешних и собственных силовых полей различной физической природы, с которыми тела непрерывно обмениваются энергией; в этом суть современной полевой трактовки физических взаимодействий. Чтобы описать такое движение в общем виде, обратимся к частному случаю: движению заряженной частицы во внешнем электромагнитном поле. Оно описывается уравнением

F ± q [u, B] + m du/dt = 0

и осуществляется, как известно, по винтовой траектории с перемен ной скоростью. Здесь F — внешняя электрическая сила; ± q — заряд частицы; u — скорость её; B — индукция магнитного поля; m du/dt — сила инерции частицы, обусловленная её массой m и ускорением du/dt = d²r/dt²; r — радиус-вектор траектории. В отсутствие энергообмена с внешней средой имеем некую разновидность движения частицы по инерции (F = 0) с постоянной поступательной скоростью u и неизменным радиусом винтовой траектории, модуль которого определяется соотношением [8] r = mu/qB.

Обобщим последний случай, чтобы включить в него движение свободной частицы с учётом взаимодействия с собственным силовым полем, природа и реальность которого обусловлены наличием у частицы массы или заряда. Для этого введём вектор K = ± qcB, где c — мировая константа, характеризующая скорость распространения света в пустоте; в результате имеем обобщённое уравнение Ньютона-Лоренца:

[u/c, K] + m du/dt = 0.       (1.13)

Тем самым мы получили одно общее уравнение, пригодное для описания зарядов и нейтральных частиц, и одновременно задали абсолютную шкалу отсчёта скорости частицы — в долях скорости света.

Теперь первое слагаемое уравнения — обобщённая сила Лоренца — выражает векторную форму закона Гука для упругого деформирования частицей или зарядом собственного силового поля как своеобразной материальной среды (не отождествлять с неподвижным мировым эфиром), в котором K — модуль упругости (жёсткость) силового поля, u/c — относительная или релятивистская его деформация. Видно, что природа этого деформирования обусловлена конечной скоростью распространения света в пустоте: при c = ∞ упругая сила в уравнении (1.13) исчезает. Радиус траектории определяется теперь соотношением

r = mu/qB = muc/K.       (1.14)

Таким образом, мы снова пришли к определению обобщённого закона инерции (1.12) в виде полевой формы его (1.13), которая провозглашает вращение в качестве природного свойства материальных частиц. При этом открытый де Бройлем корпускулярно-волновой дуализм здесь изначально получает конкретное и наглядное материальное воплощение в системе частица-поле, а классический закон инерции Галилея предстаёт в качестве предельного случая, отвечающего условию слабого влияния силового поля (дорелятивистские скорости) или полного его отсутствия у частицы: при u << c или K = 0 имеем du/dt = 0, u = const.

1.7. Модель свободного движения

На основании перестановочного свойства векторного произведения [u/c, K] = – [K, u/c] уравнение (1.13) представим в следующей форме:

[iK, iu/c] + m du/dt = 0;       (1.15)

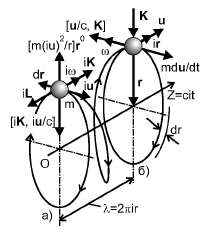
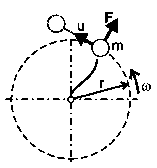
где введена мнимая единица i² = –1. Схема сил, действующих на частицу согласно уравнениям (1.13) и (1.15), изображена на рис. 1.3. Здесь сложное движение частицы по винтовой траектории радиуса r представлено в виде комбинации двух простых движений с взаимно перпендикулярными и одинаковыми по модулю векторами скорости: плоского или двухмерного вращения вокруг оси ОZ с окружной скоростью iu = dr/dt = [r, iω] (рис. 1.3, а) при центростремительном ускорении diu/dt = (u²/r)r₀ , где r₀ — единичный радиус-вектор; и одномерного поступательного движения со скоростью u = dir/dt = [r, ω] (рис. 1.3, б) вдоль оси OZ. При этом мы обрели возможность вместо уравнений математической физики в частных производных использовать для описания пространственного движения частицы более простой и удобный аппарат комплексных чисел.

Рис. 1.3.
Движение свободной частицы по винтовой траектории
может быть представлено в виде комбинации вращения (а)
и поступательного перемещения (б).

На рис. 1.3 представлено движение частицы с правой спиральностью (правый винт). Система отсчёта привязана к самой частице, о чём свидетельствует направление радиуса-вектора r от частицы к центру вращения. Равенство модулей скорости iu = u отражает одно из важнейших свойств природы — изотропию пространства в отсутствие внешних сил и полей. Умножение на мнимую единицу i согласно известному математическому правилу [15] физически означает поворот вектора на угол π/2 в направлении движения. Сечения а и б изображают положение частицы в моменты, сдвинутые на величину шага λ = 2πir винтовой траектории.

Каждому значению скорости частицы на рис. 1.3 отвечает своя траектория движения и величина её радиуса r : чем больше скорость, тем больше радиус траектории — своеобразной волны деформирования собственного силового поля частицы. Это обстоятельство позволяет нам избавиться от эйнштейновского постулата постоянства скорости света, заменив его наглядным и естественным определением с как скорости изменения радиуса траектории самовращения частицы:

с = dr/dτ = const,       (1.16)

где dr — приращение модуля радиуса-вектора r (см. рис. 1.3, б), τ — период обращения частицы. Постоянство и скалярный характер этого параметра в нашем случае отражает простой факт: самовращение частицы или тела в пустоте осуществляется строго по окружности, а радиус-вектор r в этом случае лишается определённой направленности и вырождается в псевдовектор. В результате получаем следующее простое выражение для относительной деформации силового поля:

u/c = dir/dr ≤ 1.       (1.17)

Из рис. 1.3а видно, что вращение свободной частицы со скоростью iu приводит к возникновению радиальной вращающейся силы [iK, iu/c], обусловленной упругими свойствами K поля. Эта сила уравновешивает радиальную составляющую силы инерции, связанную с наличием центростремительного ускорения частицы:

[iK, iu/c] = (m u²/r)r₀ ;       (1.18)

или, раскрывая векторное произведение [iK, iu/c] = (iK · iu/c) sinπ/2 (где π/2 — угол между векторами iK и iu), имеем:

(u/c)K = (m u²/r)r₀ .       (1.19)

А из рис. 1.3б следует, что поступательное движение частицы порождает циркуляцию силового вектора [u/c, K], который уравновешивает силу инерции частицы в направлении касательной к окружности вращения

(iu/c)K + m du/dt = 0,       (1.20)

где iu = – rω. Указанные составляющие упругой силы и обеспечивают самоподдержание режима свободного винтового движения частицы.

При этом оказывается, что во всех случаях: для любой скорости и независимо от характера движения — поступательное оно или вращательное — закон инерции описывается одним и тем же уравнением, включающим упругую и инерционную силы. Сказанное прямо приводит к общему принципу относительности Эйнштейна как следствию: «Общие законы природы должны быть выражены через уравнения, справедливые во всех координатных системах» [16]. А закон (1.13) по этой причине следует причислить к разряду фундаментальных физических законов.

[Примечание. Данный текст является продолжением диалога, начатого с автором в примечании 6 третьей главы:

Релятивистские эффекты и пространство-время .

Основная мысль, которая высказана мною в примечании 6, заключается в следующем. Нельзя из действительной части комплексной величины получить мнимую путем умножения действительной части на мнимую единицу. Действительная и мнимая части — две независимые величины единого числового агрегата. Что сделал К.П. Агафонов?

Он записывает основное уравнение своей теории в виде

[u/c, K] + m du/dt = 0.       (1.13)

Далее используется антикоммутативное свойство векторного произведения:

[u/c, K] = – [K, u/c].

И на этом основании уравнение (1.13) представляется в новом виде:

[iK, iu/c] + m du/dt = 0;       (1.15)

При этом действительные векторы u и K Агафонов К.П. превращает в мнимые iu и iK, так как он считает, что отрицательную единицу здесь можно без больших проблем представить квадратом мнимой единицы ( –1 = i² ).

С точки зрения математики уравнения (1.13) и (1.15) абсолютно тождественны. Мы же не говорим, например, что уравнения

a = bc       и       ib + d = ia/c + d

— два различных уравнения, поскольку второе уравнение получено из первого. В силу линейной зависимости уравнений (1.13) и (1.15) их различное физическое толкование исключено. Между тем К.П. Агафонов изображает на рис. 1.3 векторы [u/c, K] и [iK, iu/c] как два различных вектора, забывая, что второй был получен из первого, т.е. второй тождественно равен первому.

Автор не ограничился удвоением сущностей; в главе 6 происходит их учетверение:

F_r = - [iu/c, iK],     F_w = –[u/c, K],     iK = [iu/c, F_r],     K = [u/c, F_w].

Затем эти четыре уравнения, полученные, подчеркнем, путем тождественных математических операций, трактуются как четыре различных уравнения Максвелла:

Итак, мы видим, как К.П. Агафонов путем математических ухищрений умножает физические сущности. Ясно без всяких математических выкладок, что четыре уравнения Максвелла никак не могут быть выведены из одного уравнения. Хотя они могут образовывать четыре независимых компонента одного числового агрегата, как это показано в разделе

Симметрия уравнений Максвелла

Однако здесь уже используется более гибкий и богатый математический аппарат, оперирующий скалярами, псевдоскалярами, векторами и бивекторами. Действия с мнимой единицей ( –1 = i² ) будут недостаточны и, порою, крайне сомнительны в 3D-пространстве, базирующемся на трех ортах: i, j, k, т.е. трех взаимно перпендикулярных векторах. — О.Е. Акимов

Комментарий автора. Наш диалог выводит на вечную проблему соотношения физики и математики. Стоит ли нам в него углубляться? Неблагодарное это занятие. Вы математик, я инженер. Как в народе говорится, «кесарю кесарево, слесарю слесарево».

Убеждён в одном: физика — это наука о движении материи, для математического описания которого необходимы дифференциальное и интегральное исчисления. Но достаточны ли они? Как и Вы в своей «Симметрии уравнений Максвелла», я однажды пришёл к выводу, что «без мнимой единицы уравнения Максвелла [и не только они – К. Агафонов] неполны: они многое теряют в своей геометрической и физической интерпретации». Правда, последнее Вы просто декларируете, в то время как у меня геометрическая и физическая интерпретации предстают наглядно: например, вектор u есть поступательная составляющая винтового движения частицы, вектор iu — его вращательная составляющая.

Конечно, «с точки зрения математики уравнения (1.13) и (1.15) абсолютно тождественны». Но почему «их различное физическое толкование исключено»?. Мы то с Вами обсуждаем физическую концепцию; а с точки зрения физики они различны: одно описывает поступательное движение, другое вращательное. Хотя и то, и другое определяет единую сущность — сложное вращательно-поступательное движение материальной частицы. Иными словами, два уравнения — (1.13) и (1.15) — есть не удвоение сущностей (математика наука абстрактная и к конкретным сущностям себя не привязывает), а две стороны «одной медали» или одной сущности. Четыре уравнения Максвелла — это не учетверение сущностей, а четыре свойства одной и той же сущности — движения заряда. Наконец десять нелинейных уравнений в ОТО Эйнштейна не порождают на свет Божий десять различных сущностей: речь в ней идёт об одной сущности — тяготении. Если это не так, то Вам придётся признать, что и Максвелл с Эйнштейном (а не только К. П. Агафонов) «путем математических ухищрений умножают физические сущности».

«Ясно без всяких математических выкладок, — продолжаете Вы, — что четыре уравнения Максвелла никак не могут быть выведены из одного уравнения». Не буду переубеждать, мои аргументы приведены выше и в критикуемой Вами работе. Напомню только, что есть два метода научного исследования, называемых анализом и синтезом соответственно. Первый сводится к мысленному или фактическому расчленению целого на составные элементы; второй состоит в изучении предмета или явления как единого целого. Оба имеют право на существование. Далее додумывайте сами.

И последнее. Физика изучает материальный мир и развивается в процессе поиска истины, которая обнаруживает себя исключительно в прямом эксперименте. Математика же — только язык общения между собой неутомимых искателей физической истины. Истина одна-единственная, а методов математического оформления её множество. И это только усложняет поиск истины. Прямой аналог современному поиску физической истины представлен в Библии, в сюжете о строительстве Вавилонской башни, загубленном именно многоязычием или взаимным непониманием строителей. Предлагая новый и общедоступный язык общения или математический метод представления физических сущностей, я надеюсь обрести многочисленных последователей, которые в недалёком будущем достроят наконец эту Богом проклятую башню. — К.П. Агафонов].

1.8. Работа, энергия, КПД и законы сохранения

Теоретический анализ и расчёты в физике сильно упрощаются, если исследуемое тело или систему тел рассматривать как лишённые сил трения (П = 0) и изолированные от действия других тел и внешних сил (F = 0). Для такой системы, называемой замкнутой, уравнение (1.7) позволяет сформулировать важнейшие физические законы — законы сохранения импульса, момента импульса и полной энергии.

К понятию импульса тела приводит соотношение (1.10), если представить его в более общем виде:

F = d(mu)/dt,       (1.21)

где величина p = mu определяется как импульс или количество движения тела. Приращение импульса тела определяется величиной импульса внешней силы, воздействующей на тело в течение некоторого отрезка времени:

Fdt = dp.

При F = 0 (замкнутая система) это приводит к закону сохранения им пульса тела p = const.

Приращение момента импульса тела, вращающегося по траектории радиуса r (рис. 1.3) определяется векторным произведением

dL = [dp, r] = [Fdt, r].

Это соотношение можно представить и так:

dL/dt = [F, r].

Если на такое тело внешние силы не действуют, то момент импульса сохраняется во времени неизменным:

L = Const.

Соотношение (1.10) представим в форме Fudt = mudu и проинтегрируем за отрезок времени Δt; в результате имеем:

FuΔt = ½ mu² + W₀ .

Здесь слева стоит скалярная величина

A = FuΔt,

называемая работой силы F по перемещению тела на длине отрезка пути uΔt в направлении поступательного движения; а выражение справа включает механическую энергию W_k = ½ mu² поступательного движения, называемую кинетической энергией тела, и внутреннюю энергию W₀ , обусловленную микроструктурой и температурным состоянием тела и неизменную для рассматриваемого здесь движения.

Работа внешней силы, как видим, в рассматриваемом случае идёт на повышение кинетической энергии тела, например, при разгоне автомобиля

A = W_k = ½ mu²,

и оценивается скоростью выполнения работы или мощностью

N = A/Δt = Fu.

Когда внешняя сила F направлена на преодоление силы тяжести в процессе подъёма груза массой m на высоту h = uΔt, говорят о приращении потенциальной энергии тела

U = mgh,

где g — ускорение силы тяжести. Если по истечении отрезка времени Δt внешняя сила перестаёт действовать и система превращается в замкнутую, то полная энергия тела становится независимой от времени (закон сохранения полной энергии)

W = mgh + ½ mu² + W₀ = const.

Заметим, что кинетическая и потенциальная энергии могут быть легко преобразованы в работу, в то время как внутренняя энергия тела без разрушения его микроструктуры для получения работы непригодна. Тем не менее в инженерной практике широко используется возможность изменения внутренней энергии тела при изменении его температуры за счёт нагрева и охлаждения. На этом основана, в частности, работа двигателя внутреннего сгорания, в то время как атомная энергетика являет собой пример высвобождения внутренней энергии при разрушении связей в микроструктуре тела.

В реальных условиях не вся работа внешней силы оказывается полезной: часть её идёт на преодоление сил трения и расходуется в числе других потерь, рассеиваемых в виде тепла в окружающей среде. Эффективность полезного преобразования работы внешних сил оценивается величиной КПД (коэффициента полезного действия) процесса

η = A₀/A ≤ 1,

где A₀ — полезная часть выполненной работы в общем её балансе A. Оценка КПД каждого конкретного процесса связана с определёнными трудностями, которые демонстрируются нами в разделе 1.11 на конкретном и поучительном примере.

1.9. Глобальный характер вращения

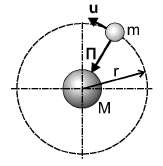
Движение материальной частицы m вблизи гравитационной массы M, схема которого представлена на рис. 1.4, является связанным посредством известной каждому школьнику силы тяготения Ньютона

П = – (GMm/r²)r₀ .

В рамках ОТО Эйнштейна оно представляется движением по инерции вдоль геодезических, простейшим случаем которых является окружность, что обусловлено неевклидовой геометрией (кривизной) пространства вблизи гравитационной массы M. Как в классической, так и в виртуальной физике такое движение признаётся абсолютным, то есть допускающим в принципе возможность измерения истинной скорости вращения частицы [3].

Движение той же частицы m вдали от гравитационной массы М в рамках СТО определяется как свободное, также осуществляемое по инерции равномерно и прямолинейно согласно первому закону динамики Ньютона. Такое движение признаётся относительным в том смысле, что скорость его может быть измерена исключительно по отношению к скорости другого свободного тела, принимаемого в качестве инерциальной системы отсчёта. Таким образом, в рамках виртуальной физики утверждается, что эти два вида движения существенно различны по физическому характеру.

Рис. 1.4.
Планетная система.

Проведём мысленный эксперимент с планетной системой рис. 1.4, оставаясь в рамках законов классической физики. Будем непрерывно уменьшать силу П, полагая, что тело M излучает энергию-массу в окружающее бесконечное пространство, заставляя частицу медленно удаляться от центра вращения и уменьшать скорость вращения согласно закону сохранения момента импульса частицы. Очевидно наступит момент, при котором указанная сила практически исчезнет, а частица, став свободной, продолжит, тем не менее, самовращение по удалённой, но той же круговой траектории в силу наличия у неё первоначального сохраняемого момента импульса. Иными словами, в классической механике характер движения связанной и свободной частицы, строго говоря, оказывается одним и тем же — вращательным, изменяются лишь радиус круговой траектории и скорость вращения частицы. Это самый простой и сильный аргумент против СТО Эйнштейна, снимающий, к тому же, следующее противоречие.

Момент импульса — это свойство вращающегося тела по определению. Когда мы говорим о вращении тела, то приписываем ему импульс р = mu и момент импульса L = mur конечной величины. А если определяем движение тела как прямолинейное, то имеем в виду нулевое значение момента импульса. Согласно же определению L в этом случае имеем бесконечное его значение; ибо прямолинейное движение есть вращение тела по траектории бесконечного радиуса r, отнюдь не нулевого.

Иными словами, для прямолинейного движения не может быть корректно определена важнейшая физическая характеристика тела L. Это означает физический запрет такого движения для объектов, обладающих массой; по-видимому, оно разрешено только для безмассовых фотонов, обладающих предельно возможной, световой скоростью c движения. На рис. 1.3 это нашло своё отражение в том, что прямолинейная траектория движения оказывается представленной мнимой величиной Z = cit, подобно четвёртой временной координате в СТО Эйнштейна. И это совпадение, по-видимому, не случайно.

Таким образом, уже в рамках строго построенной классической механики мы приходим к необходимости признания глобального характера вращения: оно является не результатом воздействия на материальную частицу внешних, в частности, только гравитационных сил, а природным свойством её, обусловленным достоверно не установленными пока причинами. Эйнштейн увидел причину в кривизне пространства-времени, окружающего массивное материальное тело, подменив тем самым физику геометрией. В нашем случае причина имеет физическую природу: упругое (без энергопотребления) взаимодействие материального тела с собственным физическим или силовым полем. Как будет показано в главе 4, это поле имеет магнитную природу, силовые линии которого и «искривляют» пространство-время вблизи массивного тела.

1.10. Пример. Инерционное «тяговое» устройство

Соотношение (1.21) может быть представлено в виде, пригодном для оценки силы тяги ракетного двигателя

F = (dm/dt)u;

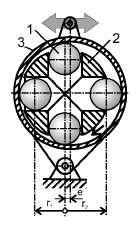
здесь u — скорость истечения газа из реактивного сопла относительно ракеты, dm/dt — секундный расход газа через сопло двигателя. Видно, что реализация больших тяговых усилий в двигателе требует создания на борту ракеты значительных запасов топлива и окислителя. Огромное число инженеров-изобретателей пытаются обойти эту проблему, опираясь на приведённую в п. 1.5 или подобную ей цитату из учебников физики и предлагая для создания тяги использовать неуравновешенную силу инерции. Пример подобного устройства представлен на рис. 1.5.

Рис. 1.5.
Конструктивная схема инерционного
тягового устройства

В устройстве используется центробежная сила, создаваемая определенным числом грузов 1, приводимых во вращение ротором 2 и удерживаемых на эксцентрической траектории направляющей системой 3, шарнирно закреплённой на борту космического аппарата. Предполагается, что тяговое усилие создаётся за счёт разности центробежных сил mω²(r₁ – r₂) от грузов, тем большей, чем больше их угловая скорость вращения ω и эксцентриситет е.

Движущая сила F, каковой в данном случае предполагается сила инерции, согласно второму закону Ньютона (1.10) придаёт грузу массой m ускорение du/dt в направлении своего действия. Таким образом, чтобы определить, может ли интересующая нас сила инерции быть движущей, надо убедиться в том, что она создаёт отличное от нуля ускорение в направлении своего действия.

Соотношения (1.9) и (1.11) такую возможность опровергают. Центробежная сила инерции относится к категории так называемых центральных сил. Их линия действия всё время проходит через одну и ту же неподвижную точку — ось вращения. Она не создаёт движения (центробежного ускорения) в направлении своего действия — вдоль радиуса-вектора r. Формально в этом можно убедиться так. Умножим слагаемые основного уравнения динамики (1.8) векторно на r. Так как векторы F и r коллинеарны, а векторное произведение коллинеарных векторов равно нулю, то в результате получаем 0 = [mr, du/dt]. При m ≠ 0 и r ≠ 0 это означает равенство нулю ускорения du/dt, создаваемого силой инерции в направлении своего действия. Тем самым подтверждается известный факт: вращение связано с центростремительным ускорением, центробежного ускорения в природе не бывает.

Рис. 1.6.
При обрыве нити груз летит в направлении
касательной к траектории вращения

Физически это понять не сложно, если вообразить картину вращения в горизонтальной плоскости груза, подвешенного на нити (рис. 1.6). Положим, что в определённый момент времени нить обрывается. Опыт показывает, что в этом случае груз летит не в направлении действия силы инерции F (радиальное направление), а по касательной к круговой траектории, в направлении скорости u. Чтобы получить малое движение (импульс) mdu в направлении центробежной силы, последняя должна сообщить грузу импульс Fdt = mdu в том же направлении. Однако в момент обрыва нити центробежная сила исчезает, то есть время её действия на оторвавшийся груз dt = 0. По этой причине отсутствует и движение груза (mdu = 0) в направлении действия силы инерции. Иными словами, последняя, будучи силой чисто внутренней, принципиально не может выполнять функции внешней или движущей силы.

Наконец самое важное состоит в следующем: центральная сила по определению не создаёт крутящего момента на оси вращения, поэтому вся энергия вращения ротора в описанном механизме идёт на преодоление сил трения. По мнению разработчиков инерционных движителей это одно из самых замечательных свойств, фактически превращающих эти устройства в источник даровой энергии: они предполагают регулируемое движение аппарата без затрат энергии на его перемещение. Мы же делаем вывод: попытки создания такого рода устройств в конечном счёте входят в противоречие с законом сохранения и превращения энергии или первым законом термодинамики и в силу этого являются совершенно бесплодными.

1.11. Пример. КПД плуга

Начало второй половины прошлого века для сельскохозяйственного машиностроения в России ознаменовано многолетней кампанией повышения рабочих скоростей машинно-тракторных агрегатов (МТА), в первую очередь пахотного. В значительной мере она была обусловлена энергетической теорией МТА, которая базировалась на следующей формуле для силы сопротивления плуга

R = fG + kab + εabu²,       (1.22)

предложенной в 1923 г. основоположником земледельческой механики В. П. Горячкиным [17]. В этом уравнении G — масса плуга; u — скорость его движения; а, b — размеры почвенного пласта; f, k, ε — коэффициенты пропорциональности. Для КПД плуга Горячкин даёт следующую формулу, названную его последователями рациональной:

η_г = ab(k + εu²) / [fG + ab(k + εu²)].       (1.23)

Она означает непрерывный рост КПД плуга при увеличении скорости пахоты: при u = 0 согласно формуле имеем

η_г = abk / (fG + abk) < 1,0,

по мере роста скорости пахоты значение η непрерывно увеличивается и при ab(k + εu²) >> fG приближается к единице.

Обратимся теперь к логике и фактам, обеспечивающим надлежащее качество всякой теории. Оптимальный по производительности и экономичности скоростной режим работы любой энергетической машины обеспечивается при наибольшем значении её общего КПД. И в случае пахотного агрегата задача оптимизации режима сводится к нахождению функции

η_т η → max.       (1.24)

где η_т — тяговый КПД трактора, η — КПД плуга.

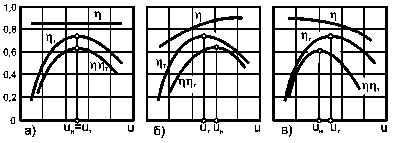
Рис. 1.7.
Положение режима оптимальной рабочей
скорости пахотного МТА в зависимости от
характера изменения КПД плуга

На рис. 1.7 представлены три возможных случая поведения функции (1.24). Если КПД плуга η сохраняется постоянным при изменении скорости (рис. 1.7, а), то максимум производительности агрегата (номинальный скоростной режим) совпадает с максимумом тягового КПД трактора (u_н = u_т); если КПД плуга с ростом скорости растёт, режим максимальной производительности должен быть смещён в сторону более высоких рабочих скоростей (u_н > u_т , рис. 1.7, б); смещение режима максимальной производительности в зону меньших рабочих скоростей (u_н < u_т , рис. 1.7, в) является признаком уменьшения КПД орудия по мере роста рабочей скорости агрегата. На практике, как показал многолетний опыт, имеет место только последний случай. Следовательно, КПД плуга по мере увеличения рабочей скорости пахотного агрегата вопреки теории Горячкина непрерывно снижается.

Как видим, уравнение (1.23) находится в грубом противоречии с результатами практического опыта. Причины его объясняются некорректностью вывода рациональной формулы (1. 22) для силы сопротивления плуга, в которой «не нашлось места» для члена с линейной зависимостью от скорости. Между тем, как показали многочисленные эксперименты, связанные с проблемой повышения рабочих скоростей, сопротивление плуга лучше описывается не двухчленном, а полным алгебраическим трёхчленом

K = K₀ + k₁u + k₂u²,

где k₁ и k₂ — коэффициенты пропорциональности. Более того, постоянный K₀ и линейный k₁u члены этого уравнения являются преобладающими, вследствие чего в практических расчётах для описания сопротивления плуга обычно пользуются приближённой линейной зависимостью типа

K ≈ K₀ + k₁u.       (1.25)

Определим далее КПД плуга как отношение сил, производящих полезную работу, к общей силе сопротивления

η = K₀ / K,       (1.26)

условно полагая первую из них равной постоянной составляющей уравнения (1. 25). Это допущение вполне логично и предполагает простое физическое содержание.

Полезная работа плуга затрачивается на изменение первоначальной структуры почвы до вполне определённой, задаваемой идеальными агротехническими требованиями. Она осуществляется за счёт подвода механической энергии от плуга к почвенному пласту и реализуется путём подрезания, переворота и крошения пласта до вполне определённой степени: недостаточная степень крошения, равно как и излишняя, является отклонением от идеальных агротехнических требований. Вследствие этого величина полезной работы определяется единственно структурой и прочностными свойствами обрабатываемой почвы; конструкция плуга и скорость пахоты определяют величину затраченной работы, в которую полезная работа входит составной и неизменной частью.

Решая (1.25) и (1.26) совместно, приходим к выражению для КПД плуга, достаточно хорошо отражающему реальный опыт:

η = 1 / [1 + u(K₀ + k₁)]

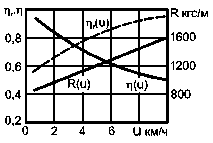
Рис. 1.8.
Характер изменения силы сопротивления
и КПД плуга от скорости агрегата

На рис. 1.8 прямой R(u) представлен характер изменения силы сопротивления плуга в соответствии с уравнением (1.25), КПД плуга согласно полученной нами формуле представлен непрерывно убывающей функцией скорости η(u), а согласно формуле В.П. Горячкина — непрерывно возрастающей функцией η_г(u).

Выводы к главе 1

• Проблема унификации физических взаимодействий находит рациональное разрешение на базе единой вязкоупругопластической модели (АКП-системы) деформирования реальных тел. Она позволяет составить два уравнения для описания процессов сжатия и сдвига сплошной среды и одно общее уравнение динамики материальной частицы.
• Принцип инерции в формулировке Ньютона является неполным, поскольку формально не учитывает вращение тел по инерции и сложное вращательно-поступательное инерционное движение. Адекватное отражение этого принципа даётся обобщённым уравнением динамики Ньютона-Лоренца.
• Силы инерции и упругости есть объективное внутреннее свойство реальных тел, проявляемое при всяком воздействии на них внешней силы или вращающего момента в виде ответной реакции на такое воздействие. Они не могут быть использованы в качестве самостоятельных движущих сил, способных производить работу без подвода к телу энергии извне.

Литература