Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Порождающая и проверочная матрицы

Откуда же берутся порождающие матрицы G? Порождающая матрица получается путем последовательного сдвига соответствующего порождающего многочлена g(x) по разрядам вправо. Последовательному сдвигу вправо отвечает умножение g(x) на xⁱ:

G = = .

Порождающая матрица G имеет размерность (k – 1) · m, поскольку для сдвига берутся степени xⁱ в пределах 0 < i < k – 1, а степень порождающего многочлена g(x) равна m. Мы знаем, что каждому порождающему многочлену соответствует проверочный многочлен h(x), который удобно записать в порядке убывания степеней:

g(x) = g₀ + g₁x + g₂x² + ... + g_mx^m, 

h(x) = h_kx^k + h_k–1 x^k–1 + ... + h₀,

причем xⁿ + 1 = g(x)h(x), где, напомним, n — общее число символов, k — число информационных, а m — число проверочных символов в кодовом слове. Если существует порождающая матрица G, то должна существовать и соответствующая ей проверочная матрица H. Действительно, такую матрицу можно получить путем последовательного сдвига проверочного многочлена h(x) влево:

H = = .

Предположим, у нас есть конкретный порождающий многочлен g(x) = 1 + x² + x³. Проверочный многочлен h(x) находится простым делением многочлена x⁷ + 1 на заданный многочлен g(x); в результате имеем: h(x)= = x⁴ + x³ + x² + 1. В соответствии с вышеприведенными определениями, находим конкретный вид порождающей G и проверочной H матриц:

G = , H = ,

GH* = (HG*)* = 0.

Последнее равенство говорит о том, что матрицы G и H ортогональны относительно друг друга (звездочка означает операцию транспонирования матрицы).

Рассмотренные G и H матрицы называются ленточными, потому что нули и единицы вдоль обеих диагоналей этих матриц образуют своеобразные ленты. Но любая ленточная матрица может быть сведена к систематическому виду:

G' = (E_{k · k} | G_{m · k}),    H' = (H_{k · m} | E_{m · m}),

где E_{k · k} и E_{m · m} — единичные матрицы.

Существует, по крайней мере, два способа сведения ленточных матриц к систематическому виду. Первый наиболее надежный способ состоит в нахождении ряда остаточных многочленов. Если r_i(x) остаточный многочлен от деления x_i на порождающий многочлен g(x), то сумма элементов r_i (x) + x_i дает строки систематической матрицы G. Аналогичным способом находятся строки проверочной матрицы H. Второй способ заключается в том, чтобы найти соответствующие линейные комбинации строк или столбцов исходных матриц ленточного типа. Найдем G и H для предыдущего случая:

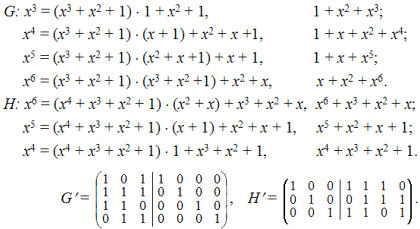
Эти две систематические матрицы можно было бы получить путем сложения векторов-столбцов исходных ленточных матриц (напоминаем, счет столбцов для G матрицы начинается с нуля, а для H матрицы — с шести).

G' :   0' = 1 + 2, 1' = 1 + 5, 2' = 3, 3' = 0, 4' = 1, 5' = 4 + 1, 6' = 6;

H' :    0' = 5, 1' = 3, 2' = 4, 3' = 2, 4' = 6, 5' = 1, 6' = 0.

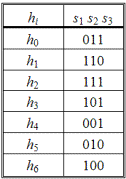
Теперь поясним, как составить проверочные соотношения и определить коды ошибок si по известной проверочной матрице. С этой целью выпишем три равенства, отвечающих строкам матрицы H' :

s₁ = h₆ + h₃ + h₂ + h₁ = 0,

s₂ = h₅ + h₂ + h₁ + h₀ = 0,

s₃ = h₄ + h₃ + h₂ + h₀ = 0.

При ошибке в символе h₀ суммы s₂ и s₃ изменятся на 1, а при ошибке в h₁ не будут равны нулю суммы s₁ и s₂. Таким образом, можно составить все коды ошибок для всех символов (табл. 2.87).

Таблица 2.87

При одновременном появлении ошибок в двух символах, например в h₅ и h₆, коды ошибок будут складываться; в данном случае он становится таким же, как и при одиночной ошибке в символе h₁. Поэтому, характеризуя код с точки зрения помехозащищенности, мы должны сказать, что он обнаруживает и исправляет любые одиночные ошибки, а также обнаруживает, но не исправляет двойные ошибки.