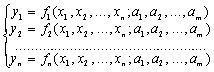Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.5. Пространственные группы и двойственность

Группы Ли и Галуа

Рассказ о группах будет неполным, если ничего не сказать о пространственных или непрерывных (континуальных) преобразованиях, теория которых оформилась несколько позже точечных (дискретных) групп, с которыми мы до сих пор имели дело. Наша ближайшая цель — показать действие принципа двойственности в сфере пространственных преобразований, который уже проявил себя в логике, но молчал в теории групп. Если при анализе точечных групп вращения треугольника, квадрата, куба и других симметричных тел мы о нем ничего не слышали, то в пространственных преобразованиях декартовых (ортогональных) и лоренцевых (гиперболических) координат он заявит о себе во весь голос. Однако прежде чем говорить о двойственности названных преобразований, нужно вспомнить, какие вообще бывают преобразования.

Основы групповых преобразований самих пространств, а не только находящихся в них симметричных геометрических тел, заложил норвежский математик Софус Ли (1842—1899). Группой преобразований Ли в самом общем ее виде называется система функциональных равенств, которая зависит от ряда пространственных координат x₁, x₂, …, x_n и совокупности параметров a₁, a₂, …, a_m:

Система преобразований Ли отличается от рассмотренного ранее линейного преобразования (2.1) только непрерывным характером изменений всех координат и параметров, что потребует от нас несколько изменить математический язык для непрерывных групп. В точечных группах были активно задействованы матрицы и подстановки, которые помогают выразить дискретную природу движения объектов, их повороты и отражения. В пространственных группах используется язык функций, которые предъявляют к себе иные требования, в частности, функции должны быть дифференцируемы. Поворот координат на бесконечно малые углы привел к инфинитезимальным преобразованиям особого вида, которые используются для получения различных законов сохранения. Группы Ли, собственно, и возникли в 70-х годах XIX в. в связи с задачей разрешимости дифференциальных уравнений в квадратурах. Успешное применение теории групп к решению алгебраических уравнений, выразившееся в победном шествии теории Галуа, привело к попытке построения своеобразного аналога теории Галуа для дифференциальных уравнений.

Теория групп, которая до сих пор рассматривалась нами, возникла благодаря усилиям французского математика Эвариста Галуа (1811—1832) при решении алгебраических уравнений высших степеней в радикалах. Решение уравнения второй степени было найдено в глубокой древности, уравнения третий (формула Кардано) и четвертой степени (формула Феррари) были решены в XVI в. В общем виде уравнение пятой степени долго не могли решить, пока, наконец, норвежский математик Нильс Хенрик Абель (1802—1829) в 1824 г. не доказал, что оно и не может быть решено в радикалах. Сразу же возник вопрос, каковы должны быть коэффициенты алгебраического уравнения, чтобы его все-таки можно было решить в радикалах? Ответ на этот вопрос как раз и дал Галуа в работе, опубликованной в 1846 г. Жозефом Лиувиллем в выпускаемом им математическом журнале.

Основная идея Галуа сводилась к следующему. Он связал алгебраическое уравнение n-й степени f_n = 0 с группой автоморфизмов, или группой Галуа Gal ( f_n ) поля корней c₁, c₂, …, c_n, которые бы оставляли без изменения поле коэффициентов уравнения a₁, a₂, …, a_n. При этом группу Галуа можно найти, не решая самого уравнения. Так, если уравнение

f₄ = x⁴ – x² + 1 = 0

имеет корень c = c₁, то его решениями будут также еще три корня:

c₂ = –c,     c₃ = 1/c,     c₄ = –1/c,

которые продиктованы симметрией коэффициентов уравнения. Группа Галуа, или группа автоморфизмов, в данном случае образована четырьмя подстановками, переставляющими индексы корней:

Gal ( f₄ ) = {a = (12)(34), b = (13)(24), c = (14)(23), e = (1)}.

Преобразование g поля G называется автоморфизмом, если преобразование суммы равно сумме преобразований и преобразование произведения равно произведению преобразований:

g(c_i + c_j) = gc_i + gc_j,     g(c_i × c_j) = gc_i × gc_j, ( c_i,c_j Î G ).

Например, преобразование поля C, переводящее каждое комплексное число a + bi в комплексно-сопряженное число a – bi является автоморфизмом поля C. Подстановки Gal ( f₄ ) действуют таким образом, что все соотношения Виета, связывающие корни и коэффициенты уравнения, остаются в силе.

Теория Галуа позволила решить многовековые проблемы, далеко выходящие за рамки решения алгебраических уравнений. Например, она ответила на вопрос, почему античные задачи о трисекции угла и удвоении куба невозможно решить с помощью линейки и циркуля. Гаусс построил с помощью этих инструментов правильный 17-угольник. Теория Галуа объяснила, почему это стало возможным, но невозможно построить правильный 7- или 13-угольники. Дело в том, что степень алгебраического уравнения

x^{p – 1} + x^{p – 2} + …+ x + 1 = 0

при простом p должна определяться выражением p = 1 + 2^2^r (теорема Гаусса). Пять чисел 3, 5, 17, 257 и 65537 удовлетворяют этому условию. Алгебра предоставляет и другие критерии инструментального построения многоугольников: многоугольники с числом сторон 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25 … с помощью циркуля и линейки построить нельзя.

Как оказалось, что конструктивная геометрия стала зависеть от алгебры уравнений? Эта зависимость устанавливается аналитической геометрией: любая задача на построение сводится к определенному виду алгебраического уравнения. Так, упомянутые задачи о трисекции угла и удвоении куба сводятся к уравнениям третьей степени. Но с помощью циркуля и линейки можно решить геометрическую задачу, если соответствующее ей алгебраическое уравнение имеет корни, выраженные только через квадратные радикалы.