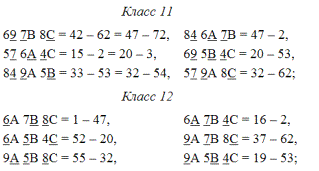Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
3.1. Группы цепей графа
Классы эквивалентности группы цепей куба
Прежде чем рассматривать группу преобразований цепей куба, установим реберный состав цепей. Цепи, привязанные к вершине a, можно разбить на три класса. Так, цепь 1 = 169845B, согласно реберной классификации, состоит из ребер следующих классов: 1222223; цепь 72 = 16AB548 имеет состав 1233222 и цепь 62 = 3845BA6 — 1222332. Две последние цепи имеют одинаковые последовательности реберных классов, только названы они сначала в прямом, потом в обратном порядке. Все три цепи принадлежат грани F гиперкуба Г72. Они могут служить представителями соответствующих классов цепей других пяти граней —
класс A: {1, 55, 52, 37, 19, 16} — 1222223;
класс B: {72, 54, 3, 42, 33, 15} — 1233222;
класс C: {62, 53, 2, 47, 32, 20} — 1222332.
Цепи первых двух классов симметричны, третьего класса — асимметричны. Симметричность цепи является ее абсолютной характеристикой; она не зависит от привязки. Ее можно установить следующим образом: для каждой цепи, начиная от вершины a, согнем вдоль соответствующих ребер реального куба жесткую проволоку, сохраняющую свою форму. Для симметричных цепей «хвост» и «голова» соответствующей изогнутой проволоки могут меняться местами, т.е. не зависимо от того, каким концом прикреплять проволоку к вершине a: всегда можно добиться того, чтобы она прошла по нужным нам ребрам. Если изогнутую проволоку от асимметричной цепи прикрепить «хвостом» к вершине a, то в любом случае, как бы ее не поворачивать, она укажет новые ребра. Таким образом, за счет вращения куба Г8 или проволоки вокруг оси, проходящей через вершину a, каждая симметричная цепь порождает только две новых цепи; асимметричная же цепь дает уже пять новых цепей.
Осуществив переход от цепей класса C к цепям класса B, мы получим первый класс реберных подстановок:
12 = 2 – 3 = 15 – 20,
31 = 62 – 72 = 42 – 47,
23 = 53 – 54 = 33 – 32.
Второй класс получается благодаря следующим преобразованиям:
9A = 1 – 72 = 52 – 53, 6A = 37 – 42 = 19 – 20,
7B = 52 – 3 = 55 – 62, 5B = 16 – 15 = 37 – 32,
4C = 55 – 54 = 1 – 2, 8C = 19 – 33 = 16 – 47.
В этом классе можно было бы отдельно выделить два подкласса: первый описывал бы переходы между цепями классов A и B, другой — между цепями классов A и C. Тогда всевозможные переходы между этими двумя подклассами породили бы третий класс:
9A 4C = 2 – 72, 6A 8C = 33 – 20,
7B 9A = 53 – 3, 5B 6A = 42 – 32,
4C 7B = 62 – 54; 8C 5B = 15 – 47.
Однако мы не будем различать подобные подклассы. Вместо этого введем классификацию подстановок в зависимости от реберной классификации. В частности, во втором классе подстановок при переходах от одной цепи к другой удаляется ребро, принадлежащее реберному перовому классу, и вводится ребро, принадлежащее второму классу. Поэтому к третьему классу отнесем подстановки, где имеют место замены, аналогичные для этого класса:
9A 8C = 37 – 55, 7B 6A = 16 – 1, 4C 5B = 19 – 52.
Из этих же соображений мы не станем делить на самостоятельные подклассы подстановки четвертого класса:
12 4C = 1 – 3, , 12 7B = 2 – 52,
23 9A = 52 – 54, , 23 4C = 53 – 55,
31 7B = 55 – 72, , 31 9A = 62 – 1,
12 6A = 15 – 19, , 12 5B = 16 – 20,
23 5B = 33 – 37, , 23 8C = 19 – 32,
31 8C = 42 – 16; , 31 6A = 37 – 47,
хотя первый из столбцов получается в результате переходов цепей, принадлежащих классам A и B, а второй — между цепями класса A и C. Ниже дается классификация всех остальных переходов между цепями, привязанными к вершине a:
Как видим, через однореберные замены, которые фигурировали в двух первоначальных 9-циклах, выражаются все многореберные подстановки данной подгруппы. Табл. 3.2 представляет собой таблицу сложения наших укрупненных классов.
Таблица 3.2
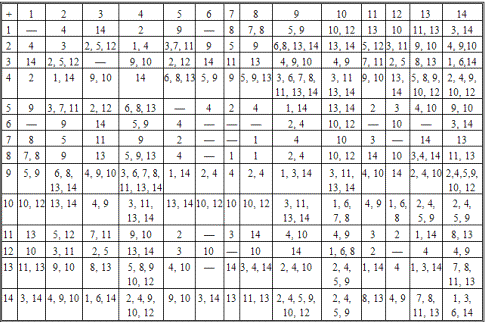
Ранее мы уже говорили, что для аддитивных групп выполняются очевидные равенства: если a + b = c, то a + c = b и b + c = a. Если это условие справедливо для отдельных подстановок, то оно будет справедливым и для целых классов. В частности, если при сложении подстановок второго и пятого классов получаются подстановки третьего, седьмого и одиннадцатого классов, т.е. если в отношении классов имеет место равенство: 2 + 5 = 3, 7, 11, то пятый класс обязательно окажется во второй строке на пересечениях 3-го, 7-го и 11-го столбцов; а поскольку табл. 3.2 симметричная, то второй класс нужно искать в пятой строке на пересечениях этих же трех столбцов. Таким образом, каждая клеточка таблицы несет двойную информацию: она указывает, во-первых, в какие классы попадают результирующие подстановки; во-вторых, где нужно искать подстановки исходных слагаемых. Поэтому, когда заполнена первая строк, мы имеем информацию не только о первом столбце, но можем проставить первый класс по всей таблице сложения. При заполнении второй строки мы узнаем, в каких клетках нужно проставить 2 и т.д.
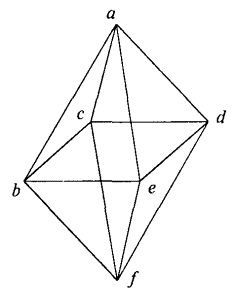
Мультипликативная группа октаэдра (рис. 3.9) та же, что и куба. Поэтому узлы Г72 можно попытаться уложить на ребра и грани октаэдра, и наоборот, большой цикл из цепей октаэдра можно уложить на кубе.
Рис. 3.9
Ребрами октаэдра определяются 120 пятизвенных цепей, что значительно больше числа семизвенных цепей куба. Это объясняется тем, что в вершинах куба соединяются три ребра, а в вершинах октаэдра — четыре: чем выше степень связи каждой вершины со всеми остальными вершинами, тем больше количество цепей.
Приведем полную мультипликативную группу вращения октаэдра (см. табл. 2.54, столбец O(6) ):
(bcde), (af)(be)(cd), (aeb)(cdf), (aed)(bfc), (aefc), e,
(bedc), (af)(bc)(de), (abe)(cfd), (ade)(bcf), (ab)(ce)(df),
(abfd), (ae)(bd)(cf), (acd)(bfe), (af)(ce), (abc)(def).
(adfb), (ad)(bf)(ce), (adc)(bef), (af)(bd),
(acfe), (ac)(bd)(ef), (acb)(dfe), (bd)(ce),
Действуя этой группой на 6-, 12- и два 8-цикла из цепей октаэдра —
6-цикл: {defbca, edfbca, bfdeca, bfdeac, bfcaed, fbcaed};
8-цикл: {abcfed, abcfde, aedfcb , aedfbc, acbfde, acbfed, adefcb, adefcb};
8-цикл: {abfedc, abfcde, aedcfb, aedcbf, aefbcd, aefdcb, abcdfe, abcdef};
12-цикл: {adcbfe, adcbef, adfebc, acbefd, acbedf, acfdeb,
abedfc, abedcf, abfcde,aedcfb, aedcbf, aefbcd},
мы получим достаточную информацию для составления большого 120-цикла, который затем можно попытаться уложить на ребра и грани куба или октаэдра.