Предсказание и открытие новых структур в спиральных галактиках

Фридман А.М.

УФН, т. 117 (2), с. 121 – 148 (февраль 2007)

Представлен обзор опубликованных за последние 20 лет работ, послуживших прогрессу в понимании природы, механизмов возникновения и наблюдаемых особенностей спирально-вихревой структуры в галактиках. Кратко описываются лабораторные эксперименты на установках с вращающейся мелкой водой, специально сконструированных по идее автора в Российском научном центре "Курчатовский институт" для моделирования возникновения спиральной структуры галактик. Обнаружение в результате этих экспериментов новых вихревых антициклонических структур послужило основой для их поиска с помощью крупнейшего в то время в мире (ныне в Европе) 6-метрового оптического телескопа БТА Специальной астрофизической обсерватории РАН. Спустя 7 лет после этих пионерских экспериментов Афанасьеву и автору настоящего обзора с помощью БТА удалось обнаружить предсказанные гигантские антициклоны в галактике Mrk 1040. Позднее были теоретически предсказаны гигантские циклоны в спиральных галактиках, впоследствии также обнаруженные на БТА. Для восстановления (реставрации) трехмерной картины распределения векторов скоростей в диске галактики на основе наблюдаемого поля лучевых скоростей (вдоль луча зрения) автором с сотрудниками был разработан метод решения задачи, относящейся к некорректным задачам астрофизики. Помимо вихревой структуры в галактиках были обнаружены другие новые структуры, в частности медленные бары, также предсказанные ранее теоретически, для чего был разработан специальный наблюдательный тест, позволяющий отличать медленные бары от исследованных ранее обычных (быстрых) баров.

1. Введение.

2. Экспериментальное моделирование генерации спиральной структуры галактик и предсказание гигантских антициклонов.

2.1. Проблема спиральной структуры галактик.

2.2. Гравигидро-динамическая концепция генерации спиральных рукавов.

2.3. Что общего между установкой "Спираль" и газовым диском галактики?

2.4. Гидродинамические неустойчивости, вызванные скачком скорости.

2.5. Моделирование генерации спиральной структуры галактик на установке "Спираль".

2.6. Вихри между спиралями на "мелкой воде".

3. Открытие гигантских антициклонов в галактиках с резким скачком на кривой вращения (на примере галактики Mrk 1040)

4. Вихри в солнечной окрестности.

5. Спирально-вихревая структура в галактиках.

5.1. Положение центров стационарных вихрей.

5.2. Как определить по одной наблюдаемой компоненте скорости все три ее компоненты?

6. Открытие антициклонов в спиральных галактиках с плавной кривой вращения.

6.1. О возможности приближения реальных спиральных возмущений в галактиках монохроматическими волнами малой амплитуды.

6.2. Наблюдательный тест: являются ли спиральные рукава волнами плотности?

6.3. Вертикальные движения в газовых дисках спиральных галактик: вертикальные скорости в волне спиральной плотности или изгибные колебания?

6.4. Поля скоростей газа в плоскости галактического диска.

7. Предсказание и открытие гигантских циклонов.

8. Существуют ли в спиральных галактиках медленные бары?

9. Наблюдаемая осцилляторная структура типа солитона огибающей в спиральном рукаве галактики NGC 1365.

10. Заключение.

Список литературы.

1. Введение

Как показали астрофизические исследования последних десятилетий, большинство эволюционных процессов, происходящих в Метагалактике, связано с коллективными эффектами. Различные неустойчивости, развивающиеся на всех масштабах иерархии структур во Вселенной, являются основной движущей силой эволюции.

Царица неустойчивостей — гравитационная неустойчивость создала всю наблюдаемую иерархию структур — от звезд и звездных скоплений до галактик и скоплений галактик. В каждом из масштабов функционируют специфические неустойчивости, создающие в системах этого масштаба собственные структуры.

Уникальным природным полигоном, на котором бурно развивается большинство из известных в Метагалактике неустойчивостей, приводящих далее к созданию регулярных структур, стационарных конвективных потоков, турбулентности и хаосу, являются астрофизические диски, среди которых особое место занимают диски спиральных галактик.

Богатство структур, наблюдаемых в дисках спиральных галактик, является следствием многочисленных развивающихся в этих дисках коллективных процессов, как линейных, так и нелинейных. Большинство из них встречается в астрономических объектах других масштабов, но не всегда столь явно себя проявляет, как в спиральных галактиках — уникальной природной лаборатории коллективных явлений. Некоторые из этих неустойчивостей изучаются также в физике, механике и математике. Именно поэтому нам кажется, что изложенные в настоящем обзоре наблюдательные и теоретические открытия последних лет являются важными и интересными для широкого круга астрономов, физиков, механиков и математиков.

Работа "Предсказание и открытие новых структур в спиральных галактиках", удостоенная Государственной премии РФ в 2003 г., представляет собой цикл работ, который был начат более 30 лет назад (в 1972 г.) и выполнялся под руководством автора обзора. Творческий коллектив включал в себя наблюдателей, интерпретаторов астрономических данных, теоретиков и экспериментаторов, объединенных выполнением единой научной задачи.

Новые структуры, предсказанные и открытые этим коллективом, — это гигантские вихри (циклоны и антициклоны) и медленные бары в спиральных галактиках. Вихри были обнаружены в двумерном поле скоростей газовых дисков спиральных галактик. Для доказательства существования медленных баров необходимо было построить кривую вращения газового диска с учетом движения газа в тех же крупномасштабных вихрях. Таким образом, для открытия упомянутых выше галактических структур потребовались измерения и анализ поля лучевых скоростей в плоскости галактических дисков.

До начала работы над данной проблемой на 6-метровом телескопе БТА (Большой телескоп азимутальный) Специальной астрофизической лаборатории (САО) РАН измерения полей скоростей галактик производились с помощью спектрографа с длинной щелью. Сложение результатов измерений, полученных при различной ориентации щели, приводило к погрешностям, не позволяющим достичь необходимой точности оценки систематических отклонений скоростей газа от ожидаемых при круговых движениях в галактике.

В САО РАН совместно с Марсельской обсерваторией (Франция) был создан комплекс аппаратуры, включающий интерферометр Фабри-Перо, для высокоточных измерений полей скоростей газа галактик по доплеровскому смещению эмиссионных линий с точностью не хуже 10 км с ^–1. Подобной аппаратуры до этого в России не существовало. Только с ее помощью и могли быть сделаны открытия новых галактических структур.

В настоящем обзоре изложены некоторые детали предсказания и открытия новых структур в спиральных галактиках, дано описание ряда научных проблем, которые потребовалось решить на этом пути, представлены перспективы в понимании физики галактики.

В данном обзоре мы старались по возможности избегать специальной терминологии и сложных математических выкладок. Более строгое изложение можно найти в оригинальных статьях, указанных в списке литературы.

2. Экспериментальное моделирование генерации спиральной структуры галактик и предсказание гигантских антициклонов

Вихри между спиралями, удивительно напоминающими спиральные рукава галактик, впервые были обнаружены на настольной установке с вращающейся "мелкой водой", которая была создана в Российском научном центре "Курчатовский институт" E.H. Снежкиным специально для моделирования процесса генерации спиральных рукавов галактик и потому получила название "Спираль" (рис. 1а, б). В первой модификации этой установки центральная часть имеет форму конуса при почти плоской периферийной части, во второй — обе части выполнены в виде параболоидов. Жидкость вовлекается дном во вращение, между центральной частью и периферией в жидкости образуется скачок скорости вращения с радиусом R и шириной близкой к глубине жидкости H₀. В результате слой мелкой воды приобретает скачок на радиальном профиле скорости вращения (рис. 1в), имитирующий скачок на кривой вращения галактики, способный вызвать генерацию (в результате гидродинамической неустойчивости) спиральных волн плотности. Это позволило использовать установку "Спираль" для моделирования динамических процессов в газовом галактическом диске со скачком скорости вращения.

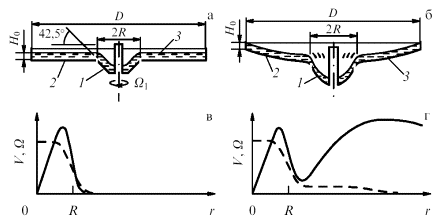
Рис. 1. Первая (а) и вторая (б) модификации установки "Спираль": 1 — центральная часть, вращающаяся с угловой скоростью обнаружим часть, вращающаяся с угловой скоростью Ω₁, 2 — наружная часть, вращающаяся с угловой скоростью Ω₂, 3 — слой мелкой воды; на рис. а: D = 30 см, R = 4 см; на рис. б: D = 60 см, R = 8 см. Схематические изображения радиальных профилей с сильным скачком скорости вращения мелкой воды (в) и газового галактического диска (г): сплошные кривые соответствуют линейной скорости вращения, штриховые — угловой. Антициклоны (д) между спиральными волнами плотности на мелкой воде установки "Спираль": трем спиральным рукавам соответствуют три антициклона.

Перед экспериментаторами ставилась задача проверить возможность генерации спиральных волн плотности гравигидродинамической неустойчивостью, которая в реальных галактиках может быть связана с наблюдаемыми во многих случаях быстрыми локальными падениями (скачками) скорости вращения газа в галактиках, хорошо заметными на кривых вращения галактик, полученных ранее на БТА [1]. Схематически сильный скачок скорости изображен на рис. 1г. Из наблюдений следовало, что (с учетом углового разрешения телескопа) около половины спиральных галактик имеют относительные скачки скорости Δv/v на кривой вращения не менее 10 — 15%. Однако, как показали численные расчеты Баева и Фридмана [2], в механизме образования спиральных рукавов в газовых дисках галактик с такими скачками скорости гидродинамические эффекты играют не менее важную роль, чем гравитационные.

Такая точка зрения на природу возникновения спиральных рукавов в галактиках, высказанная автором в 1972 г. (см. [3] и цитированную там литературу), отличалась от точки зрения чисто "гравитационной" теории генерации спиральных рукавов, принимающей во внимание лишь силы самогравитации [4]. В гравитационной теории не учитывались наблюдаемые (порой весьма значительные!) градиенты основных параметров диска.

Прежде всего на установке "Спираль" была проверена справедливость основных положений гравигидродинамической теории спиральной структуры: связь относительной величины скачка скорости вращения Δv/v и относительного размера пространственной области его локализации ΔR/R с числом генерируемых спиральных рукавов. Для этого на установке был создан скачок скорости вращения, имитирующий наблюдаемые скачки на кривых вращения галактик (рис. 1в). Вращающаяся на установке мелкая вода описывается уравнениями двумерной газодинамики [5]. В этом состоит динамическое родство вращающейся мелкой воды с газовым диском спиральных галактик, что и послужило отправной идеей для моделирования. (Строго говоря, теоретической основой для моделирования являлась тождественность динамических уравнений газового самогравитирующего диска и вращающейся мелкой воды [6, 7].)

Результаты модельного эксперимента на мелкой воде [8] не только подтвердили правильность гравигидродинамической теории генерации спиральной структуры, но и привели к неожиданным и оригинальным решениям некоторых вопросов, связанных с такими особенностями спиральной структуры, как ветвление рукавов и редко наблюдаемые "лидирующие" спирали. Более того, они дали и нечто принципиально новое: между спиральными рукавами на мелкой воде были обнаружены антициклонические вихри [9] (рис. 1д). Значит, такие вихри должны наблюдаться и в реальных спиральных галактиках! Почему же их не могли обнаружить в течение всего времени изучения спиральной структуры, т.е. в течение более чем полутора столетий? Постараемся ответить на этот вопрос, обратившись к истории исследований спиральных галактик.

2.1. Проблема спиральной структуры галактик

В 1845 г. лорд Росс в своем родовом имении Бер-Касл в Ирландии спроектировал и построил 183-сантиметровый рефлектор с фокусным расстоянием 17 м, долго остававшийся самым большим телескопом в мире, что позволило Россу впервые описать спиральную структуру многих туманностей, которые в течение еще семи последующих десятилетий считались принадлежащими нашей звездной системе. И только в 1924 г. Эдвин Хаббл с помощью крупнейшего по тем временам телескопа обсерватории на горе Вильсон (США) с диаметром зеркала 2,5 м надежно установил, что туманности того же типа, как и те, в которых Росс обнаружил спиральную структуру, являются отдельными спиральными галактиками.

Примерно в то же время в известной книге Астрономия и космология [10] Джине пишет о том, что, по его мнению, "в спиральных туманностях действуют совершенно неизвестные нам силы", которые только и могут объяснить "неудачу при попытках понять происхождение спиральных ветвей".

Основная трудность здесь состояла в том, что галактические диски, в плоскости которых расположены спиральные рукава, вращаются дифференциально: с удалением от центра галактики угловая скорость вращения падает — в основной области диска обратно пропорционально расстоянию от центра. Это означает, что если спиральные рукава — уплотнения из газа и молодых звезд — вращались бы так же дифференциально, как и газовый диск, в котором они наблюдаются, то со временем они растянулись бы настолько, что после 1 – 2 оборотов периферии диска спиральные рукава стали бы уже с трудом отличимыми от фона. Между тем наша спиральная Галактика в окрестности Солнца совершила порядка 50 оборотов, сохранив четко выраженную спиральную структуру.

В 1938 г. Бертилу Линдбладу удалось разрешить этот парадокс. Он предположил, что спиральные рукава галактик — это волны плотности. Волновой фронт по определению вращается с постоянной угловой скоростью. Поэтому в дифференциально вращающемся диске никакого "растяжения" волны нет.

Позднее волновая теория спиральных рукавов Линдблада была переоткрыта Лином и Шу, которые совместно с сотрудниками существенно развили эту теорию, поставив перед наблюдателями ряд принципиальных вопросов. Главный из них — определение угловой скорости вращения спирального узора. В гравитационной концепции эта величина не находится — она является свободным параметром, определяемым из наблюдений. Ее нахождение равносильно определению радиуса коротационной окружности, на которой постоянная угловая скорость спиралей совпадает с угловой скоростью дифференциально вращающегося галактического диска. Лишь недавно членами нашего творческого коллектива были опубликованы статьи с описанием канонического метода определения этого важнейшего параметра в спиральных галактиках [11, 12]. В разделе 4 мы кратко изложим этот метод, позволивший нам решить одну из основных задач — найти предсказанные антициклоны в газовых дисках спиральных галактик. Однако сначала мы попытаемся изложить суть некоторого обобщения чисто гравитационной концепции образования спиральной структуры.

2.2. Гравигидродинамическая концепция генерации спиральных рукавов

Гравигидродинамическая концепция [3, 6, 13], включающая в себя гравитационную концепцию как частный случай, учитывает силу самогравитации, а также градиенты основных невозмущенных параметров — плотности и скорости вращения, которыми в чисто гравитационной концепции пренебрегается. На рисунке 2а, б изображены радиальные профили линейной скорости вращения и поверхностной плотности для нашей Галактики. Относительная величина скачка скорости вращения в центральной области газового диска) на расстоянии от 0,4 кпк до 1,2 кпк от центра) составляет примерно 40 %, а величина скачка поверхностной плотности газа в области максимального градиента скорости (на расстоянии примерно 0,7 кпк от центра) составляет почти два порядка. Как можно пренебрегать такими градиентами, если в этом случае гидродинамическая неустойчивость оказывается намного сильнее гравитационной?

Рис. 2. (а) Профиль наблюдаемой скорости вращения нашей Галактики с двумя скачками скорости [14]: один из них, больший, максимум отрицательной производной скорости которого локализован на 0,7 кпк, находится недалеко от центра, другой, более удаленный, принадлежит солнечной окрестности, (б) Профиль плотности в газовом диске нашей Галактики; М0 — масса Солнца, равная 1,989 х 10 ³⁰ кг. (в) Кривые вращения различных галактик, имеющих скачок скорости вращения, построенные по данным ранних наблюдений на БТА.

Членами нашего коллектива были проведены исследования кривых вращения (т.е. зависимостей скорости вращения от радиуса) спиральных галактик на 6-метровом телескопе [1]. Как отмечалось выше, из произвольной выборки спиральных галактик примерно в половине случаев на кривой вращения наблюдаются скачки скорости, превышающие 10 – 15%. На рисунке 2в изображены профили вращения некоторых галактик. Такие скачки скорости могут приводить к развитию центробежной неустойчивости [6, 8, 9, 13], генерирующей спиральные волны плотности — спиральные рукава галактик.

Центробежная неустойчивость относится к классу неустойчивостей сдвиговых течений. Как правило, необходимым условием роста крупномасштабных возмущений в таких неустойчивостях является условие kL < 1, где k — волновой вектор возмущений вдоль скачка скорости, L — ширина "размазки" сдвигового течения. Так как k = 2π/λ, где λ — длина волны возмущения, то условие неустойчивости означает малость ширины сдвигового течения L по сравнению с длиной волны. В результате неустойчивости величина L "размывается" до тех пор, пока не будет достигнута граница устойчивости, при которой могут существовать лишь волны, удовлетворяющие условию

k_φ L = 1,      (1)

здесь k_φ — азимутальное волновое число (в диске галактики координата вдоль скачка скорости — это азимутальный угол φ). По определению

k_φ = m/R,      (2)

где m — число рукавов галактики, R — радиус, на котором происходит скачок скорости.

Если теперь ввести параметр q = Ω₂/Ω₁ где Ω₁, Ω₂ — угловые скорости вращения центра и периферии галактики (до и после скачка скорости соответственно), то, очевидно, величина "размазки" L будет тем больше, чем больше скачок угловой скорости вращения, т.е. чем меньше параметр q. Качественно такую зависимость можно записать в виде

L ~ Aq ^–α, α > 0,      (3)

здесь A — некоторая постоянная.

Подставляя (2) и (3) в (1), получаем качественную зависимость между числом рукавов и безразмерной величиной скачка скорости q:

m ~ Rq ^–α/A, α > 0.      (4)

Соотношение (4) означает, что чем больший скачок скорости имеет галактика (т.е. чем меньше величина q), тем меньше у нее рукавов.

В гравигидродинамической теории получена точная формула связи между m и q, корректность которой была проверена как для спиральных галактик с известными кривыми вращения, так и в эксперименте с вращающейся мелкой водой. Однако прежде, чем перейти к эксперименту, мы должны убедиться в том, что он действительно является "модельным" для процесса генерации спиральных рукавов галактик в рамках гравигидродинамической концепции. В таком случае естественно возникает вопрос, который вынесен в заголовок раздела 2.3.

2.3. Что общего между установкой "Спираль" и газовым диском галактики?

Со ссылкой на замечательную книгу Гидродинамика [5] Ландау и Лифшица мы уже отмечали одно общее свойство мелкой воды и газового галактического диска. Однако можно указать и два принципиальных различия.

Первое состоит в том, что установка "Спираль" имеет дно, из-за чего мелкая вода испытывает придонную вязкость, характеризующуюся числом Экмана. Ничего подобного, очевидно, нет у газового галактического диска. С другой стороны, в галактическом диске действуют силы самогравитации, отсутствующие в мелкой воде установки "Спираль".

В работе [6] показано, что оба этих "принципиальных" различия оказываются иллюзорными. Во-первых, число Экмана на установке "Спираль" является малым, т.е. мала придонная вязкость. Однако главным, пожалуй, оказывается то, что время вязкого затухания возмущений на мелкой воде "Спирали" много больше времени развития центробежной неустойчивости. Другими словами, придонная вязкость не оказывает влияния на процесс генерации (в результате развития неустойчивости) спиральных волн плотности на мелкой воде. С другой стороны, не будь вообще придонной вязкости, мы не смогли бы столь простым способом заставить вращающуюся жидкость сформировать нужный нам профиль скорости кругового вращения со скачком. В спиральных галактиках профиль скорости вращения газового диска создается гравитационным потенциалом, в основном звездных подсистем, как значительно более массивных (см., например, [15]). В этом смысле звездные подсистемы в создании кривой вращения газового диска играют ту же роль, что и дно в установке "Спираль". Что касается роли вязкости при генерации спиральных рукавов реальных галактик в газовом диске, то она пренебрежимо мала как при развитии центробежной неустойчивости, вызванной градиентом скорости, так и при гравитационной неустойчивости в отсутствие заметных градиентов скорости. В отсутствие выше названных неустойчивостей вязкость может приводить к образованию структур, что имеет место, например, в кольцах планет [14]. Однако мы не знаем случая генерации за счет вязкости крупномасштабных спиральных рукавов в галактике.

Обратимся теперь ко второму "фундаментальному" различию мелкой воды и газового галактического диска, связанному с наличием в последнем сил самогравитации. В работе [6] в систему исходных динамических уравнений для самогравитирующего газового диска была введена новая величина — скорость звука в самогравитирующей среде. Эта величина меньше скорости звука в среде несамогравитирующей, поскольку упругие свойства газа — способность расширяться при начальном сжатии газового элемента — ухудшаются в самогравитирующей среде: сжатый элемент удерживается гравитационными силами. Уравнения для галактического диска при замене скорости звука в самогравитирующем газе характерной скоростью распространения волны на мелкой воде превращаются в уравнения для мелкой воды.

Из выше изложенного следует, что установка "Спираль" с вращающейся мелкой водой действительно может использоваться для лабораторного моделирования процесса генерации спиральной структуры в газовом галактическом диске, вызванного развитием гидродинамической неустойчивости из-за наличия градиента скорости вращения.

2.4. Гидродинамические неустойчивости, вызванные скачком скорости

На рисунке 3 изображены возмущения тангенциального разрыва скорости v, направленной вдоль оси x, в двух противоположных предельных случаях, когда число Маха M = v/с, где с — скорость звука, много меньше (рис. 3а) и много больше (рис. 3б) единицы. Согласно Ландау [17] амплитуды возмущений по обе стороны оси z от плоскости z = 0 тангенциального разрыва падают экспоненциально, ~ exp(–z/z₀). Поэтому достаточно ограничиться областью |z| < z₀.

а)

б)

Рис. 3. Схематические изображения распределения скорости по разные стороны от возмущенного тангенциального (а) дозвукового и (б) сверхзвукового разрыва.

Область I (над "горбом" возмущения) на рис. 3а, б можно рассматривать как область движения внутри сопла (точнее, продольной половины сопла). При этом характер течения в двух соплах — дозвуковом и сверхзвуковом — принципиально различен [18]. В наиболее узком (критическом) сечении дозвукового сопла скорость максимальна так же, как она максимальна в наиболее узком течении реки. В критическом сечении сверхзвукового диффузора скорость, наоборот, минимальна. Отсюда — различная динамика двух тангенциальных разрывов скорости, дозвукового и сверхзвукового, основанная на постоянстве интеграла движения Бернулли v²/2 + W= const, где W — энтальпия. В дозвуковом течении скорость под "горбом" меньше, чем скорость над "горбом", v_II < v_I, следовательно, W_II > W_I. Поскольку в обычных ситуациях давление возрастает с ростом энтальпии, то P_II > P_I, т.е. "горб" под действием перепада давления будет продолжать расти. В этом состоит физика неустойчивости тангенциального разрыва скорости, или при более плавном профиле скорости — неустойчивости Кельвина – Гельмгольца [19].

В случае сверхзвукового скачка скорости (рис. 36) мы пишем обратное неравенство P_II < P_I, т.е. "горб" подавляется градиентом давления — неустойчивость отсутствует. На эффект стабилизации неустойчивости сверхзвукового тангенциального разрыва скорости первым обратил внимание Ландау [17]. Этот эффект имеет место в двумерной среде, такой как тонкий газовый слой или мелкая вода. В реальной трехмерной среде эффект стабилизации также существует, но начинает сказываться лишь при больших числах Маха [19].

Наблюдаемые скачки скорости в газовых дисках галактик — сверхзвуковые (типичное значение скорости звука или дисперсии скоростей облаков в межзвездном газе около 10 км с ^–1, в то время как скорость вращения газовых дисков примерно 200 км с ^–1). Поэтому для таких дисков выполняется критерий стабилизации Ландау — неустойчивость тангенциального разрыва скорости, или неустойчивость Кельвина-Гельмгольца, в них отсутствует. Однако присутствует другая неустойчивость — центробежная, которая развивается при сколь угодно больших числах Маха при условии, что угловая скорость вращения центральной части (внутренней по отношению к скачку скорости) больше, чем периферии: q = Ω₂/Ω₁ < 1. Это условие всегда выполняется для дисков спиральных галактик.

Итак, если на мелкой воде мы создадим скачок скорости вращения, больший характерной скорости распространения возмущений на мелкой воде, то это будет аналогично созданию сверхзвукового скачка скорости в газовом диске галактике, т.е. как раз тому, что наблюдается в спиральных галактиках [1]. Результаты этого эксперимента мы рассмотрим сразу после того, как будет кратко описана сама экспериментальная установка и метод диагностики спиральных волн плотности и поля скоростей на мелкой воде.

2.5. Моделирование генерации спиральной структуры галактик на установке "Спираль"

2.5.1. Установки "Спираль" и диагностика. Обе модификации установки "Спираль" имеют одинаковую принципиальную схему — круглый сосуд, состоящий из двух частей: "центральной части" и "периферии", причем центральная часть может вращаться независимо от периферии. В первой модификации центральная часть имеет форму конуса, а периферийная часть практически плоская (рис. 1а). Во второй модификации (рис. 1б) обе части состоят из двух параболоидов с размерами вдвое большими соответствующих размеров первой модификации. Жидкость вовлекается дном во вращение, между центральной частью и периферией в жидкости образуется на радиусе R скачок скорости вращения с начальной шириной, близкой к глубине жидкости H₀. В результате слой мелкой воды имеет скачок на радиальном профиле скорости вращения (рис. 1в). Используемая на "Спирали" диагностика дает возможность определить как структуру волн плотности, так и поле возмущенных скоростей мелкой воды.

В сосуд с белым дном наливается зеленый раствор; при черно-белом фотографировании через красный светофильтр участки "горбов" волн плотности выглядят темнее участков "впадин". Поле скоростей определяется по направлению и длине треков (за время экспозиции) плавающих на поверхности жидкости бумажных кружков диаметром 1–2 мм. Фотоаппарат вращается с регулируемой угловой скоростью, при этом ось его вращения совпадает с осью вращения "Спирали". Подробнее установки "Спираль", диагностика и эксперименты на мелкой воде описаны в [20].

2.5.2. Связь между числом рукавов и величиной скачка скорости. Согласие гидродинамической теории генерации спиральной структуры с результатами модельного эксперимента демонстрируется на рис. 4а, где мы видим, что в соответствии с формулой (4) число спиральных рукавов увеличивается с возрастанием параметра q.

2.5.3. Отстающие и лидирующие спирали. Различные виды спирального узора галактик характеризуются не только числом спиральных рукавов, но и своей формой. Прежде всего различают "отстающие" и "лидирующие" спирали (рис. 4б, в). Первые вращаются концами назад и поэтому имеют хорошую "аэродинамическую" форму. Подавляющее большинство спиральных рукавов относится к отстающим спиралям.

Рис. 4. Спиральные волны плотности (а), генерируемые на мелкой воде установки "Спираль" центробежной неустойчивостью вследствие скачка скорости q = Ω₂/Ω₁ < 1, где Ω₁ и Ω₂ — угловые скорости вращения центральной части и периферии соответственно; с уменьшением скачка скорости (увеличением параметра q) число спиральных рукавов возрастает (см. формулу (4)) (увеличение q слева направо). Схематические изображения отстающих (б), лидирующих (в) спиралей (стрелкой указано направление вращения диска галактики) и возможного механизма возбуждения (г) лидирующих спиралей.

Используя произвольную выборку из 109 спиральных галактик, И. Паша показал, что лишь три из них имеют лидирующие спирали [21]. При этом у каждой из этих трех галактик есть близкий спутник, но только для одной из них удалось измерить направление орбитального момента спутника относительно направления "спина" самой галактики: они оказались противоположными.

Изменив на установке "Спираль" знак угловой скорости вращения периферии, мы обнаружили лидирующие спиральные волны плотности. Автором настоящего обзора была высказана идея о том, что в редко встречающихся галактиках с лидирующими спиралями роль контрвращающегося внешнего диска может играть спутник, возмущающий основной диск галактики, если он вращается в плоскости галактики в противоположном направлении (рис. 4г).

2.5.4. Ветвление спиралей. Это явление настолько распространенное, что его отсутствие скорее можно отнести к разряду исключений. Как правило, ветвление происходит "наружу": двигаясь вдоль рукава к периферии, встречаем область, в которой рукав раздваивается. Именно такую картину мы видим на фотографии спирального узора на мелкой воде (рис. 5а). Напомним, что различным, но постоянным в момент фотографирования значениям q соответствует разное число спиральных рукавов. В отличие от фотографии, представленной на рис. 1д, при получении которой величина скачка q не менялась, здесь снимок сделан в момент, когда параметр q уменьшается. При этом если в начальный момент величина q соответствовала границе неустойчивости, генерирующей четырехрукавные волны (m = 4), то в момент фотографирования генерируются двухрукавные волны (m = 2). Генерация волн происходит на скачке скорости, где мы и видим моду m = 2. Периферия, как всегда, с запозданием узнает, что центр уже перестроился на другую моду, и потому на перефирии мы видим еще старую моду (m = 4). В результате возникает "ветвление", что отражает эволюцию диска: увеличение скорости его центральной части по сравнению со скоростью на периферии или, наоборот, относительное уменьшение скорости на периферии. Первое возможно, например, при сжатии центральной части, второе — при расширении периферии.

Рис. 5. Ветвление спиральных рукавов на мелкой воде установки "Спираль" в процессе изменения величины скачка скорости (а) и линии тока в случае генерации двухрукавной волны плотности: (б) фотоаппарат неподвижен относительно вращающейся мелкой воды, (в) фотоаппарат вращается с угловой скоростью вращения спиралей.

2.6. Вихри между спиралями на "мелкой воде"

Неподвижный фотоаппарат фиксировал траектории частиц (линии тока), которые часто встречаются в астрономических работах, посвященных полю скоростей в галактиках, и являются малоинформативными, (рис. 56). Фотоаппарат, вращающийся вместе со спиральными рукавами, т.е. с одинаковой с ними угловой скоростью, зафиксировал антициклоны (рис. 5в).

3. Открытие гигантских антициклонов в галактиках с резким скачком на кривой вращения (на примере галактики Mrk 1040).

Тождественность уравнений для мелкой воды и газового галактического диска [6], количественное согласие результатов эксперимента по исследованию зависимости числа генерируемых спиралей от числа Маха [8] на скачке скорости, экспериментальное подтверждение чисто "астрономических" гипотез о происхождении ветвлений и лидирующих спиралей — все это свидетельствует в пользу того, что вращающаяся мелкая вода на установке "Спираль" прекрасно моделирует динамические процессы и структуры в газовых дисках спиральных галактик. Поэтому появление на поверхности мелкой воды между спиральными рукавами антициклонов, всего лишь раза в два меньших по размеру рукавов, не оставляло сомнений в том, что аналогичные вихри существуют в спиральных галактиках. А раз так, значит, задача состоит в их обнаружении.

Зададимся вопросом: каким условиям должна удовлетворять спиральная галактика как первый кандидат на обнаружение вихрей?

Как видно из результатов эксперимента, центры антициклонов находятся на скачке скорости, а структуры — спирали и вихри — вызываются гидродинамической неустойчивостью. Поэтому следовало найти галактику с большим скачком скорости вращения, который, без сомнения, вызывал бы эту неустойчивость.

Но не только этому условию должна была удовлетворять спиральная галактика — первый кандидат на обнаружение вихрей. Она должна быть "удачно ориентирована" в пространстве по отношению к наблюдателю (рис. 6а). Поясним, что это означает.

Рис. 6. (а) Координаты, используемые для описания положения галактики относительно наблюдателя и положений отдельных участков газа в плоскости галактического диска. Угол наклона галактики i — угол между картинной плоскостью (плоскостью, перпендикулярной лучу зрения) и плоскостью галактики; х', у' — декартовы координаты в картинной плоскости; х, у — декартовы координаты в плоскости галактики; r, φ — полярные координаты в плоскости галактики, r — галактоцентрический радиус, φ — галактоцентрический азимутальный угол, отсчитываемый от большой линии галактики (она же "линия узлов") — линии пересечения плоскости галактики и картинной плоскости. Направление луча зрения совпадает с направлением оси z'. (б) Карта тангенциальной скорости v_танг ~ v_набл/(cos φ sin i) – v_вращ, v_набл — скорость вдоль луча зрения. Центры антициклонов, изображенных кривыми в форме эллипсов со стрелками, расположены сравнительно недалеко от линии узлов, (в) Сравнение усредненной по азимуту кривой вращения с распределением скоростей вдоль линии узлов (темные кружки) в галактике Mrk 1040.

Антициклоны, которые мы хотим обнаружить, в неподвижной относительно спиральных рукавов системе координат характеризуются наличием замкнутых линий тока в плоскости галактического диска с центрами на радиусе коротации. На этом радиусе скорость вращения диска относительно спиральных рукавов равна нулю. Отлична от нуля только возмущенная скорость газовых облаков, вызванная той же самой неустойчивостью, которая образовала спиральные волны плотности и вихри.

Если бы мы смогли измерить, например, только возмущенную азимутальную скорость, то для двухрукавной галактики мы увидели бы симметрично расположенные по обе стороны от центра на коротационной окружности две гипотетические точки, во внутренней и внешней окрестности каждой из которых возмущенные азимутальные скорости имеют противоположные направления. Это свойство можно использовать как наблюдательный критерий наличия антициклона в диске галактики.

Однако для каждого облака мы измеряем с помощью доплеровского смещения только лучевую компоненту скорости, лежащую на прямой, соединяющей облако с телескопом. В общем случае кроме азимутальной скорости в лучевую скорость вносят вклад еще две компоненты скорости облака: радиальная и z-компонента (направленная вдоль оси вращения). Вместе с тем, если бы газовый галактический диск был ориентирован так, что азимутальные возмущенные скорости в окрестности центров вихрей оказались бы направленными вдоль луча зрения, а радиальная и z-компонента — перпендикулярно ему, то вклад последних в лучевую скорость равнялся бы нулю. Мы измеряли бы только азимутальную скорость. Вклад z-компоненты скорости отсутствует, если мы наблюдаем диск практически с ребра (i = π/2). Вклад радиальной скорости в области центров вихрей отсутствует, если центры вихрей лежат практически на линии узлов (большой динамической оси) галактики (рис. 6а).

Именно этим условиям ориентации по отношению к наземному наблюдателю удовлетворяет галактика Mrk 1040, имеющая аномально большой и резкий скачок скорости вращения.

Действительно, угол наклона плоскости этой галактики к лучу зрения, который составляет ~ 73°, только на 17° отличается от угла при ее виде с ребра. Как мы видим из рис. 6б, центры антициклонов (последние отмечены замкнутыми кривыми со стрелками) расположены недалеко от линии узлов [22].

Скачок лучевой скорости вдоль линии узлов, т.е. там, где локализованы вихри, как видно из рис. 6в, составляет огромную величину — более 150 км с ^–1, т.е. Δv/v > 0,6. Усредненная по азимуту скорость вращения имеет скачок Δv/v ~ 0,3. Радиальный градиент скорости также аномально велик: d (ln v)/d (ln r) ~ –3,1, что соответствует очень сильной гидродинамической неустойчивости [13].

4. Вихри в солнечной окрестности

Как уже говорилось, для выявления галактических антициклонов необходимо найти поле скоростей в системе координат, вращающейся вместе со спиральным узором. В экспериментах на установке "Спираль" скорость вращения спиральных рукавов могла быть непосредственно измерена. Однако для реальных галактик определение этой скорости представляет собой отдельную и очень нелегкую задачу. Дело в том, что характерные времена обращения галактических дисков составляют около ста миллионов лет, поэтому за любое разумное время наблюдения невозможно зафиксировать величину смещения спиральных рукавов вследствие их вращения.

Задача определения скорости вращения спирального узора эквивалентна нахождению радиуса коротации, т.е. радиуса, на котором галактический диск вращается с той же скоростью, что и спирали. Если спиральная волна образуется в результате неустойчивости, вызванной скачком скорости, то ее радиус коротации совпадает с положением скачка [6, 13]. Наличие в галактике Mrk 1040 аномально резкого скачка на кривой вращения и заведомо выполняющихся условий гидродинамической неустойчивости сразу снимало вопрос о положении радиуса коротации в этой галактике и облегчало выявление в ней гигантских антициклонов [22]. Тем не менее для большинства внешних галактик вопрос о положении радиуса коротации остается открытым.

Поэтому неудивительно, что следующей в списке кандидатов на обнаружение вихревых структур стала наша собственная Галактика, для которой вопрос о положении радиуса коротации наиболее изучен.

Для определения радиуса коротации в этом случае используются данные о так называемом градиенте возрастов звезд. Звездообразование происходит главным образом в спиральных рукавах, поэтому в них наблюдается повышенная концентрация молодых, только что родившихся звезд. По мере старения звезды все более удаляются от спиральных рукавов. Поскольку угловая скорость вращения газового диска вокруг центра Галактики падает при уменьшении расстояния от центра, а спиральный узор вращается как единое целое с постоянной угловой скоростью, то область диска внутри коротационной окружности обгоняет спиральные рукава, а область диска вне нее отстает от них. Звезды обладают "памятью" о газовом диске, из которого они образовались, вследствие чего на расстояниях от центра Галактики, меньших радиуса коротации звезды движутся быстрее, чем спиральные рукава, а на расстояниях, больших радиуса коротации, — медленнее. В результате чего направления градиентов возраста звезд по обе стороны от коротационной окружности должны быть противоположными (рис. 7) (см. пояснение в подписи к рисунку).

Рис. 7. Градиент возраста звезд в окрестности коротационной окружности. Область повышенной концентрации молодых звезд (изображенная сплошной линией) совпадает с наблюдаемой локализацией спирального рукава. Более старые, ранее родившиеся в этом рукаве звезды уже переместились от рукава к области, показанной штриховой линией. Их треки обозначены маленькими стрелками, длина и направление которых определяются скоростью вращения диска в системе отсчета, связанной с рукавом; большой стрелкой показано направление вращения Галактики в лабораторной системе координат. Внутри коротационной окружности (штрихпунктирная окружность) диск вращается быстрее спирального рукава, поэтому направление малых стрелок здесь совпадает с направлением большой стрелки. Вне коротационной окружности направление малых стрелок - противоположное. Градиент возраста звезд ориентирован по направлению малых стрелок, поэтому радиус, на котором он меняет направление, соответствует радиусу коротации (штрихпунктирная окружность).

Описанная выше особенность градиента возрастов была обнаружена в окрестности Солнца [23, 24], что указывает на положение радиуса коротации, достаточно близкое к солнечному кругу (орбите Солнца вокруг центра Галактики). Исследования поля лучевых скоростей цефеид в солнечной окрестности также показали, что в этой области азимутальная скорость спирального узора в Галактике совпадает со скоростью вращения диска [25]. Таким образом, мы видим, что разные исследователи приходят к единому выводу о том, что Солнце находится вблизи от радиуса коротации.

Кроме этого, наблюдаемая кривая вращения газового диска нашей Галактики имеет депрессию как раз в окрестности солнечной орбиты. На основании этих двух фактов было высказано предположение [26], что в окрестности галактической орбиты Солнца находятся центры гигантских антициклонов.

Эта гипотеза была проверена на основании данных о лучевых скоростях 316 молекулярных облаков, 256 классических цефеид и 106 молодых открытых скоплений [11] (рис. 8а).

На рисунке 8б показана кривая вращения, полученная в модели чисто кругового движения [27]. Более детальные исследования показали, что отклонения скоростей от полученных в модели чисто кругового движения имеют систематический характер и коррелируют с наблюдаемыми спиральными структурами.

На рисунке 8в показано модельное поле скоростей в системе отсчета, вращающейся с угловой скоростью, равной средней угловой скорости вращения звезд вблизи Солнца [11]. Это поле скоростей имеет форму антициклона, центр которого лежит в солнечной окрестности.

Следует отметить, что в нашей Галактике изучению поля скоростей диска мешает межзвездная пыль, поглощающая свет. Это приводит к тому, что мы можем исследовать лишь небольшую область Галактики и практически не видим участков Галактики с противоположной стороны от ее центра.

Наблюдения внешних галактик позволяют увидеть всю галактику одновременно, что дает возможность более точно определить ее характеристики. И именно в этом направлении необходимо было продолжить исследования.

Рис. 8. (а) Поле лучевых (т.е. направленных по лучу зрения) скоростей, полученное из наблюдательных данных для звезд и газа [11]; координаты Солнца (0, 8). (б) Круговая скорость вращения как функция галактоцентрического радиуса r. Треугольники — данные наблюдений, сплошная кривая — усредненная кривая вращения; вблизи радиуса Солнца (здесь он полагается равным 8,5 кпк) наблюдается депрессия скорости [27]. (в) Модельное поле скоростей, полученное по движению звезд и газа [11]. (г) Переход из инерциальной системы координат в неинерциальную, вращающуюся с угловой скоростью спирального узора Ω_ph. Сплошными кривыми показаны невозмущенная азимутальная скорость в диске галактики Ω(r)r для наблюдателя, находящегося в центре галактики, и азимутальная скорость в неинерциальной системе v_circ, обращающаяся в нуль на радиусе коротации.

5. Спирально-вихревая структура в галактиках

Обнаружение предсказанных ранее антициклонов в газовом диске Mrk 1040 и солнечной окрестности нашей Галактики было достаточно естественным. В обоих случаях наблюдаемая кривая вращения газового диска имеет область резкого падения (депрессии) на некотором радиусе. Наличие такой области указывает либо на существование скачка на реальной кривой вращения, что может приводить к развитию гидродинамической неустойчивости, либо на существование заметных локальных отклонений от кругового движения. Именно первый случай моделировался экспериментально на установке "Спираль", где впервые были обнаружены вихревые структуры.

Однако, как указывалось в разделе 3, галактика Mrk 1040 демонстрирует аномально большой скачок скорости, причем при наличии близкого спутника. В случае же солнечной окрестности бедность статистических данных приводит к такой величине ошибок, которая не дает возможности ссылаться на факт обнаружения антициклона как на строго доказанный.

В таком случае обнаруженные антициклоны могли бы считаться некими особыми структурами, присущими лишь пекулярным галактикам с резкими скачками скорости вращения и не являющимися непременным атрибутом любой спиральной галактики с волновой природой спиралей.

Простое качественное рассуждение показывает, что это не так и газовые вихри являются неотъемлемой принадлежностью спиральных волн плотности вне зависимости от природы действующих в диске сил: гидродинамических, сил самогравитации либо приливных, вызванных, например, баром или спутником галактики (более строгое, математическое доказательство этого факта см. в [28]).

Предположим, что в результате какого-либо коллективного механизма (неустойчивости) в диске галактики возникают возмущения скоростей и плотности. Пока амплитуды возмущений малы, их рост описывается линейной теорией неустойчивости. Тогда все возмущенные величины можно легко выразить через одну, т.е. они являются пропорциональными друг другу. При этом поле возмущенных скоростей диска, перенося часть вещества из одних областей диска в другие, создает в одних местах сгущения в виде спиральных рукавов плотности, а в других — спиральные области пониженной плотности.

В результате дальнейшего увеличения амплитуды возмущенных величин плотность газа в спиральных рукавах может возрасти в несколько раз, сформировав нелинейную волну плотности, которую мы наблюдаем как спиральный рукав. Однако, как следует из наблюдений, величины возмущенных скоростей в обоих дисках, газовом и звездном, оказываются много меньше скорости вращения. Возрастание возмущений приводит к стабилизации неустойчивости, и спиральная волна становится квазистационарной. Особенности поля скоростей, вызванные такой волной, удобнее всего исследовать в системе отсчета, вращающейся с угловой скоростью спирального узора Ω_ph (рис. 8г). Эта вращающаяся система координат замечательна прежде всего тем, что в ней спиральные рукава оказываются неподвижными, т.е. возмущенная поверхностная плотность диска и связанные с ней линейными соотношениями компоненты возмущенной скорости могут быть записаны как функции, не зависящие от времени:

        (5)

где r — галактоцентрический радиус, φ — азимутальный угол, отсчитываемый от большой динамической оси галактики (рис. 6в), C_i — амплитуда, а F_i — фаза i-го параметра. Для определенности мы ограничились случаем двухрукавной галактики.

Поскольку диск галактики вращается дифференциально, внутренняя часть диска (до радиуса коротации) будет вращаться быстрее, чем спиральный узор, а внешняя, напротив, — медленнее (рис. 8г). Наблюдатель, находящийся на радиусе коротации r_c, будет видеть, что угловые скорости диска по обе стороны от окружности коротации направлены в противоположные стороны. В соответствии с (5), при каждом значении радиуса возмущенная поверхностная плотность σ(φ) четырежды (удвоенное число спиральных ветвей) меняет свой знак с изменением азимутального угла. Соответственно этому радиальная скорость также четырежды меняет знак. В результате вблизи области коротации, где величина полной азимутальной скорости невелика, возникают замкнутые линии тока — вихри (рис. 9а). Поскольку газ в них движется в направлении, противоположном направлению вращения диска, они являются антициклонами (рис. 9б).

Рис. 9. (а) Схема расположения двух антициклонов вблизи радиуса коротации в системе координат, вращающейся с угловой скоростью двухрукавного спирального узора. Знак возмущенной плотности σ меняется на каждом радиусе вдоль азимутального угла четыре раза (на рукавах — знак плюс, между ними — минус), (б) Схематические траектории частиц, стрелками показано направление их движения в циклоне и антициклоне.

Следует подчеркнуть, что эти антициклоны нельзя рассматривать как математическую особенность принятой модели вращения, в которой положение замкнутых траекторий полностью определяется заданием угловой скорости системы отсчета. Только в области действительной коротации межзвездный газ в своем движении не пересекает спиральных ветвей, поэтому потоки газа (при условии малой дисперсии скоростей по сравнению со скоростью вращения) обречены там постоянно двигаться либо в окрестности определенной спиральной ветви, либо между ветвями. Наличие вихревых движений в области коротации — это физическая особенность галактик. Поэтому эволюция звездообразования и содержание газа в области коротации представляет особый интерес, но эти вопросы выходят за рамки настоящего обзора.

Таким образом, во всем диске малые возмущенные скорости выполняют "свою работу", собирая вещество в ярко светящиеся рукава, но сами никак не проявляются, будучи "задавленными" большой круговой скоростью диска. Только на радиусе коротации, где круговая скорость газа становится малой в системе координат вращающейся спирали, возмущенные скорости проявляются в виде гигантских антициклонов. Это наглядно демонстрирует то, что спирали и вихри суть разные проявления единого коллективного механизма, название которого — волны плотности.

Описанная выше качественная картина формирования антициклонов в дисках галактик основана только на одном предположении — предположении о волновой природе спиральной структуры. Поэтому вихревые структуры должны быть универсальным атрибутом спиральных галактик вне зависимости от состава диска (газ или звезды) и механизма генерации волны плотности.

5.1. Положение центров стационарных вихрей

Итак, мы показали, что гигантские антициклонические вихри являются полноправной составляющей крупномасштабной структуры спиральных галактик. Однако интерес к галактическим вихрям вызван не только фактом наличия этих новых структур в спиральных галактиках, но и той уникальной информацией, которую можно получить из их анализа. Замечательным свойством гигантских антициклонов является зависимость положения их центров относительно спиральных рукавов (рис. 10а-в) от механизма образования волновых структур.

Причину такой зависимости легко понять уже из общих соображений. Действительно, существование стационарных некруговых движений требует определенного баланса сил. Распределение сил, в свою очередь, определяется распределением плотности — спиральным узором — и тем, силы какой природы — самогравитация или силы давления – преобладают.

Рис. 10. Схема расположения вихрей относительно спиральных рукавов в двухрукавной волне плотности: вихри на спиралях (а), между спиралями (б), промежуточное положение вихрей (в). Тонкими сплошными кривыми со стрелками показано движение частиц в вихрях, жирные сплошные кривые — линии одинаковой плотности в спиральных рукавах. Если момент вращения диска в области коротации возрастает с радиусом, то случай рис. а соответствует преобладанию сил самогравитации, случай рис. б — сил давления, а случай рис. в реализуется, когда в области коротации существенную роль играют приливные силы. Когда угловой момент возрастает с радиусом (г), если радиальная скорость v_r направлена к центру, то азимутальная сила F_φ ориентирована против направления вращения, а если v_r направлена от центра, то F_φ ориентирована по направлению вращения. В случае азимутальных сил, направленных от центра вихря, если в диске превалируют силы гидродинамического давления (градиент давления), то в центре вихря должен быть максимум давления и поверхностной плотности (д), а если превалируют силы гравитации F_g, то в центре вихря должен находиться минимум поверхностной плотности (е).

Чтобы понять общие закономерности, задающие азимутальное положение вихрей относительно спиральных рукавов, рассмотрим участки, на которых газ движется строго радиально (рис. 10 г). Распределение удельного углового момента, определяемого в нулевом приближении скоростью вращения диска, M = Ωr ² неоднородно по радиусу. В результате переход газовой частицы на другой радиус требует изменения ее углового момента, т.е. азимутальные силы, действующие на частицу, должны ее "подкручивать" или, наоборот, тормозить в зависимости от того, движется ли она в сторону увеличения или уменьшения момента вращения диска. На рисунке 10 г показано направление сил, действующих на частицу, для случая, когда момент вращения возрастает с радиусом.

Азимутальная сила, действующая на частицу газа, определяется азимутальным поведением возмущений давления Р и гравитационного потенциала Ф, вызванных волной плотности, а также, возможно, внешней приливной силой F_внеш , действующей на газ при наличии у галактики спутника или сильного бара:

        (6)

Следовательно, если преобладающими являются силы давления, то баланс сил, необходимый для стационарного существования антициклонического вихря, будет достигаться при расположении центра вихря в максимуме возмущенного давления (рис. 10д). Поскольку положение максимума давления в спиральной волне совпадает с положением максимума плотности, это означает, что вихрь расположен на спиральном рукаве (рис. 10а). Та же закономерность хорошо известна в метеорологии: с антициклонами в земной атмосфере связаны области повышенного давления, а с циклонами — пониженного.

Если плотность газа на некотором участке диска возрастет, то пробные частицы, находящиеся в диске, будут испытывать дополнительное гравитационное притяжение к этому объему, т.е. возмущенная гравитационная сила направлена в сторону увеличения плотности (рис. 10е). Следовательно, если спиральная волна имеет гравитационную природу и в области коротации преобладают силы самогравитации, то центры антициклонов должны располагаться в минимуме плотности, т.е. между спиральными рукавами (рис. 10б).

Если в области коротации существенное влияние оказывают внешние приливные силы, то центры антициклонов окажутся не совпадающими ни с максимумом, ни с минимумом плотности (рис. 10в).

Если удельный момент вращения в области коротации убывает с радиусом, что возможно при очень резком падении угловой скорости вращения, то направление азимутальной силы, необходимой для стационарного существования антициклона, меняется на противоположное по сравнению с изображенным на рис. 10 г. Соответственно, обратным будет и расположение центров вихрей относительно спиральных рукавов (табл.).

Таблица. Расположение центра вихря относительно спиральных рукавов в зависимости от направления роста удельного углового момента диска и от того, какие из сил преобладают: силы гидродинамического давления или силы самогравитации.

Имеющиеся сведения о закономерностях проявления галактических антициклонов полностью согласуются с приведенным выше анализом. Лабораторное моделирование на мелкой воде [9] проводилось для случая, когда в области радиуса коротации наблюдалось резкое падение скорости вращения, что соответствует убывающему с радиусом угловому моменту, dM/dr < 0. Поэтому вихревые структуры наблюдались между спиралями. Численное моделирование (см., например, [2]) показало, что и в газовых галактических дисках с кривыми вращения, имеющими резкий скачок угловой скорости, вихревые структуры находятся между спиральными рукавами плотности. Именно между спиралями были обнаружены антициклоны в галактике Mrk l040 (см. раздел 3). В работе [29] проведено численное моделирование гидродинамической неустойчивости, приводящей к генерации спиральных волн в дисках с достаточно плавными кривыми вращения, dM/dr > 0. Вихревые структуры возбуждались одновременно со спиральными рукавами и располагались на них.

Задача о замкнутых бананоподобных траекториях звезд в гравитационном поле спиральной волны, соответствующих вихревым структурам в звездном диске, была рассмотрена Контопулосом [30]. Для случая малых амплитуд спирального гравитационного потенциала в дисках, момент которых возрастает с радиусом, им было получено, что вихревые структуры должны находиться между спиралями. Таким образом, положение вихрей в звездных и газовых самогравитирующих дисках совпадает (см. табл., строка "самогравитация").

Естественно, может возникнуть вопрос: если вихревые структуры должны существовать во всех галактиках, где имеются спиральные волны плотности, и их обнаружение дает столь ценную информацию о динамических свойствах галактики, то почему мы можем назвать лишь один-два объекта, для которых указание на существование таких структур следует из наблюдений?

Причина состоит в несоизмеримости усилий обнаружения вихревых структур по сравнению с обнаружением спиральных. В первом случае необходимо решить целый комплекс задач как чисто наблюдательных, так и связанных с методами обработки полученных данных. В частности, необходимо определить такой важный фундаментальный параметр, как радиус коротации спирального узора.

Как уже упоминалось в разделе 4, если спиральная структура обязана своим появлением гидродинамической неустойчивости на скачке скорости, то положение радиуса коротации совпадает с положением скачка. (Заметим, что наблюдаемый скачок на кривой вращения может в некоторых случаях и не отражать реальную особенность изменения равновесной круговой скорости с изменением r, а являться следствием возмущения поля скоростей волной плотности.) Однако если кривая вращения галактики гладкая, то радиус коротации не может быть найден независимо. В работе [12] было показано, что в последнем случае для определения радиуса коротации и обнаружения гигантских антициклонов требуется восстановить поле полного (трехкомпонентного) вектора скорости в газовом диске галактики.

5.2. Как определить по одной наблюдаемой компоненте скорости все три ее компоненты?

Проблема определения полного вектора скорости связана с тем, что в астрономии для далеких объектов мы можем напрямую определять скорость только по доплеровскому смещению в наблюдаемых спектральных линиях. Таким образом, известна только одна компонента скорости — вдоль луча зрения. Для восстановления других компонент скорости нужна некоторая модель объекта. <...>

6. Открытие антициклонов в спиральных галактиках с плавной кривой вращения

6.1. О возможности приближения реальных спиральных возмущений в галактиках монохроматическими волнами малой амплитуды.

Как следует из раздела 5, первым шагом восстановления поля скоростей газового диска галактик является проверка применимости для реальных галактик с регулярной структурой упрощенного описания в виде монохроматического возмущения (8) – (11). Большинство спиральных галактик являются двухрукавными. Поэтому проверка включает в себя две части:
• проверка наличия замыкания по амплитуде в фурье-спектре поверхностной плотности второй гармоники;
• проверка наличия замыкания по амплитуде в фурье-спектре поля лучевых скоростей первых трех гармоник (см. соотношения (13) – (18)).

На рисунке 13 показаны спектры карт поверхностной яркости галактики NGC 157 в ближнем инфракрасном (К) диапазоне (рис. 13а) и NGC 1365 в линии нейтрального водорода 21 см (рис. 13б). Как видно из рисунка, в обеих галактиках имеется отчетливое преобладание второй фурье-гармоники поверхностной яркости, что означает преобладание той же гармоники в спектре поверхностной плотности σ.

Рис. 13. Фурье-спектры аксиально-несимметричной части карт поверхностной яркости галактик NGC 157 в К-диапазоне (а) и NGC 1365 в линии 21 см (б). Фурье-спектры полей лучевых скоростей галактик NGC 157 (в) и NGC 1365 (г), представленных на рис. 11.

Появление в спектре лучевой скорости первых трех гармоник является следствием эффекта проекции. С математической точки зрения это происходит за счет умножения при проекции на луч зрения монохроматических, зависящих от 2φ компонент вектора скорости газа на также монохроматические функции аргумента φ (cos φ и sin φ). Таким образом, проверка преобладания в спектре лучевой скорости первых трех гармоник является, по существу, проверкой замыкания по амплитуде второй гармоники в компонентах вектора скорости v_r , v_φ и v_z.

На рисунке 13в, г приведены фурье-спектры полей лучевых скоростей галактик NGC 157 и NGC 1365 за вычетом вкладов систематической скорости и чисто кругового движения газа (точнее, вклада первой четной гармоники). Первое из полей получено в линии ионизированного водорода H_α, а второе — в линии нейтрального водорода 21 см. В обоих случаях видно преобладание первых трех гармоник, что подтверждает хорошую точность описания реальных спиральных возмущений в галактиках как монохроматических.

6.2. Наблюдательный тест: являются ли спиральные рукава волнами плотности?

Тест, представленный в разделе 6.1, свидетельствует о возможности описания реальных спиральных возмущений одной фурье-гармоникой. Это свойство позволяет восстановить полное векторное поле скоростей газа по однокомпонентному полю лучевой скорости (см. раздел 5). Однако восстановленное таким образом поле скоростей может оказаться не более чем "мгновенным снимком", мало что говорящим о сложных процессах, идущих в галактическом диске. Тем не менее, если спиральное возмущение является волной плотности, то ситуация резко меняется — восстановленное поле после перехода в систему координат, ковращающуюся со спиральным узором, оказывается стационарным и полностью характеризующим динамическое состояние диска.

Таким образом, мы приходим к необходимости наблюдательной проверки того, является ли спиральная структура данной галактики волной плотности. В разделе 2 мы писали о том, что гипотеза Линдблада о волновой природе спиральных рукавов разрешила парадокс неразмывания спиральной структуры дифференциальным вращением. В разделе 4 был приведен наблюдательный тест по проверке гипотезы о волновой природе спирального рукава нашей Галактики — смена знака градиента возраста звезд на коротационной окружности внутри спирального рукава (см. рис. 7). Там же было отмечено, что этот тест применим лишь в солнечной окрестности нашей Галактики. А как быть с наблюдательной проверкой волновой природы спиральных рукавов в других галактиках?

В данном разделе мы опишем один из предложенных нами наблюдательных тестов по определению волновой природы спиральных рукавов галактик [11, 12]. В предлагаемом методе кроме теории собственных колебаний диска используется также соотношение между наблюдаемой лучевой скоростью газового диска и возмущенными компонентами скорости газа. <...>

6.3. Вертикальные движения в газовых дисках спиральных галактик: вертикальные скорости в волне спиральной плотности или изгибные колебания?

Рассмотренный в разделе 6.2 тест доказывает связь с двухрукавной волной плотности первой и третьей фурье-гармоник поля лучевой скорости, определяемых движениями в плоскости диска. Именно эти движения и интересуют нас с точки зрения выявления гигантских антициклонов, аналогичных тем, что наблюдались в экспериментах с мелкой водой. Однако, для того чтобы можно было ограничиться учетом только этих гармоник, требуется показать, что вторая фурье-гармоника вызвана вертикальными движениями в той же волне плотности. В данном разделе приведен пример использования для этой цели одного из разработанных нами наблюдательных тестов [34].

Чтобы прояснить основную идею этого наблюдательного теста, приведем некоторые сведения из теории колебаний галактических дисков.

Известно два типа вертикальных движений в дисках галактик, возбуждаемых совершенно различными механизмами [35]. Первый из них связан с волнами плотности и вместе с уже рассмотренными нами движениями в плоскости диска составляет единое трехкомпонентное векторное поле скоростей в спиральной волне плотности. Этот тип движений не деформирует центральную плоскость диска z = 0, поскольку компонента скорости v_z в волне плотности является нечетной функцией z: v_z (–z) = –v_z (z), так что v_z = 0 в плоскости z = 0.

Второй тип вертикальных движений приводит к изгибу диска наподобие поверхности колеблющейся мембраны. Вертикальная скорость при таком движении является четной функцией координаты поперек диска z: v_z (–z) = v_z (z), и v_z ≠ 0 в плоскости z = 0. Такое поведение газового диска может быть вызвано либо приливным влиянием галактики-спутника, либо соответствующим движением звездного диска, в который погружен газовый.

В звездном диске мембранные (изгибные) колебания возбуждаются так называемой шланговой неустойчивостью, возникающей в случае, когда дисперсия скоростей звезд в плоскости диска существенно больше, чем в вертикальном направлении. Небольшой начальный изгиб диска в этом случае усиливается в результате действия центробежной силы, действующей на звезды, движущиеся по искривленным траекториям. Точно таким же образом центробежные силы искривляют пожарный шланг с быстро текущей по нему водой, откуда и возникло название данной неустойчивости.

Таким образом, мы должны выяснить, какой из типов вертикальных движений, различающихся классом симметрии функции v (z) по отношению к плоскости z = 0, наблюдается в газовом диске спиральных галактик и приводит к появлению второй фурье-гармоники в спектре поля лучевой скорости. Для решения этой задачи естественно прежде всего выбрать галактику, ориентированную к наблюдателю так, чтобы именно вертикальная скорость v (z) давала основной вклад в наблюдаемую скорость по лучу зрения. Затем мы должны провести измерения лучевой скорости таким образом, чтобы иметь различные результаты при различной симметрии v_z (z).

Первое требование выполняется, если галактика имеет малый угол наклона i (так называемые галактики, видимые "плашмя"), поскольку отношение вкладов вертикальной скорости и скорости в плоскости диска пропорционально cos i.

Что же касается метода, чувствительного к симметрии v_z, то он может состоять в сравнении результатов измерения одного и того же поля вертикальной скорости в разных диапазонах длин волн при различной степени прозрачности газового диска. Для одного из волновых диапазонов оптическая толщина диска должна быть меньше единицы, а для другого — больше. Этим требованиям удовлетворяют, например, измерения скорости по доплеровскому сдвигу линии 21 см и линии H_α.

Поясним, какого рода различия в результатах измерений можно ожидать при использовании разных диапазонов длин волн в дисках с разной оптической толщиной при том или ином типе вертикального движения газа в диске галактики.

В линии H_α из-за большой оптической толщины диска для этой линии мы видим главным образом его ближайшую к нам часть. Поэтому для обоих типов вертикальных движений измерение в линии H_α даст максимальное значение вертикальной скорости. Действительно, в случае своего нечетного поведения vz равна нулю в плоскости z = 0 и возрастает с удалением от этой плоскости, достигая максимума на краю диска, т.е. там, где мы и измеряем ее с помощью линии H_α. Величина v_z в изгибных колебаниях практически не зависит от z (с точностью до 2πz/λ << 1, где λ — длина волны [35]).

Когда измерения проводятся с помощью линии 21 см, для которой диск почти прозрачен, вклады участков диска по разные стороны от центральной плоскости z = 0 примерно равны по величине. В случае нечетного поведения v_z (z) будет происходить взаимное погашение этих вкладов — участки с противоположными вертикальными скоростями будут вызывать доплеровский сдвиг линии в противоположные стороны, оставляя ее максимум несдвинутым. Следовательно, для вертикальных движений в волне плотности лучевая скорость (за вычетом системной скорости галактики), измеренная в линии 21 см, будет существенно меньше измеренной в линии H_α. В случае же мембранных колебаний и четного поведения v_z (z) результаты измерений в обеих линиях должны быть близки друг другу, т.е. практически совпадать.

Описанный наблюдательный тест определения природы вертикальных движений в диске галактики был проверен при исследовании поля скоростей спиральной галактики NGC 3631, которая имеет отчетливую двухрукавную структуру (рис. 15а) и ориентирована почти "плашмя" (i = 17°). Данная галактика является изолированной, что исключает возможность ее искажения приливными силами.

Наблюдения в линии H_α, использованные в данном исследовании, были получены на 6-метровом телескопе САО РАН [33, 34]. Наблюдения с использованием линии 21 см были выполнены Дж. Кнапеном на Westerbork Synthesis Radio Telescope [36]. Наблюдения в оптическом диапазоне (H_α) и радиодиапазоне (21 см) в силу ряда технических причин имели существенно различное угловое разрешение (2" и 15,2" х 11). Поэтому для более адекватного сравнения было выполнено сглаживание оптического поля лучевых скоростей до разрешения 13", сравнимого с таковым для радиоданных. Исходное оптическое поле, сглаженное оптическое поле и радиополе лучевых скоростей галактики NGC3631 показаны соответственно на рис. 15б-г.

Рис. 15. (а) Изображение спиральной галактики NGC 3631 в R-диапазоне (из архива телескопа им. Исаака Ньютона (Канарские острова)). (б) Поля лучевых скоростей газа в этой галактике, полученные из измерений в линии H_α с высоким угловым разрешением, ~ 2", (в) из тех же измерений, но сглаженных до разрешения ~ 2", и (г) из измерений в линии 21 см с разрешением 15,2 х 11". Вклад различных фурье-гармоник в отклонения поля лучевых скоростей этой галактики от чисто кругового движения, усредненный по области диска (r < 80 "): (д) поле скоростей в линии H_α с высоким угловым разрешением, (е) сглаженное поле скоростей в линии H_α, (ж) поле скоростей в линии 21 см.

Фурье-спектры всех полей, представленных на рис. 15б–г, демонстрируют преобладание первых трех гармоник (рис. 15д–ж), что является следствием двухрукавной спиральной структуры в данной галактике (см. соотношения (13)-(18)).

Результаты, представленные на рис. 15д–ж, согласуются с предположением, что вторая фурье-гармоника поля лучевой скорости обязана своим присутствием вертикальным движениям газа в диске NGC 3631. Действительно, для данных в линии H_α, представленных на рис. 15д,е, только вторая гармоника имеет заметную амплитуду, что и должно быть, если эта гармоника вызвана вертикальными движениями, в то время как первая и третья гармоники вызваны движениями в плоскости диска, вклад которых оказывается подавленным из-за эффекта проекции (проекция этих скоростей на луч зрения пропорциональна sin/)• Для NGC3631 sin i ~ 0,3. В то же время значение амплитуды второй гармоники поля лучевой скорости, полученного по радиоданным, существенно ниже (рис. 15ж).

Сравнивая рис. 15д, е и ж, приходим к выводу, что меньшие амплитуды первой и третьей гармоник поля скоростей в линии 21 см по сравнению с амплитудами исходного поля в линии H_α связаны с влиянием разрешения — эти гармоники имеют близкие амплитуды в поле лучевых скоростей в линии 21 см (рис. 15ж) и сглаженном поле скоростей в линии H_α. Вторая гармоника в поле лучевых скоростей в линии 21 см существенно меньше, чем в сглаженном поле скоростей в линии H_α (рис. 15е). Это свидетельствует в пользу того, что в NGC3631 мы наблюдаем вертикальные движения в волне плотности, а не изгибные колебания [33, 34].

6.4. Поля скоростей газа в плоскости галактического диска

Как следует из разделов 6.1–6.3, все независимые наблюдательные тесты говорят в пользу применимости разработанного нами метода для восстановления полного векторного поля скоростей газа в спиральных галактиках с регулярной спиральной структурой по полю лучевой скорости.

К настоящему времени проведена обработка полей лучевой скорости и восстановление полного вектора скорости около десяти спиральных галактик — среди них NGC157, NGC6148, NGC1365, NGC3893 и др. [11, 33, 37–40]. Во всех случаях независимые способы дали согласующиеся между собой результаты. Это позволило выйти на совершенно другой уровень доказательности полученных результатов. В астрономии невозможно "потрогать" изучаемые объекты или поставить на них эксперименты, как это делается в физике (за исключением ближайших объектов солнечной системы). Совпадение между собой результатов нескольких независимых способов анализа наблюдательных данных может служить доказательством корректности используемой модели.

При ошибке определения скорости в элементе изображения порядка 15 км с ^–1 и использовании более 105 определений скоростей удалось детектировать амплитуды скоростей в спиральных рукавах — 20–30 км с ^–1 с точностью 2–5 км с ^–1.

Восстановление скоростей позволяет сразу решить две классические задачи: определить радиус коротации и дать прямое доказательство волновой структуры наблюдаемых спиральных рукавов. Кроме того, этот метод позволил решить также ряд новых задач. Одной из важнейших задач является обнаружение в галактиках новых структур — гигантских антициклонов.

На рисунке 16 для двух галактик NGC157 и NGC1365 приведены поля скоростей в плоскости газового диска в системе координат, вращающейся с угловой скоростью спирального узора, наложенные на депроецированные изображения соответствующих галактик. Если сам спиральный узор является стационарным или квазистационарным, то данное поле скоростей также будет стационарным или достаточно медленно изменяющимся со временем. Как видно из рис. 16, в обоих случаях вблизи радиуса коротации наблюдаются два хорошо выраженных антициклона. Именно такие антициклонические вихри были предсказаны на основании лабораторных экспериментов на мелкой воде. Центры антициклонов находятся на радиусе коротации.

Рис. 16. Поле скоростей газа в плоскости диска галактик: (а) NGC157, наложенное на карту ее поверхностной яркости в линии На, (б) NGC 1365, наложенное на карту ее поверхностной яркости в линии 21 см.

Обратим внимание на то, что возмущенные скорости газа в спиральных ветвях на радиусах, меньших радиуса коротации, направлены к центру, а на радиусах, больших радиуса коротации, — от центра галактик. Именно такое поведение скоростей и предсказывается теорией волн плотности.

Сравнение положения спиральных ветвей с положением антициклонов показывает, что центры антициклонов находятся между спиральными рукавами. Последнее означает, что для данных галактик силы самогравитации в газе превышают силы гидродинамического давления (см. табл.).

Анализ, подобный представленному в настоящем обзоре, пока может быть проведен лишь для очень небольшого числа галактик. Но он наглядно продемонстрировал большие возможности, которые открывает метод исследования фурье-компонент азимутального распределения лучевой скорости, когда для этого имеется достаточный массив наблюдательных данных.

Несмотря на единство спирально-вихревой структуры, открытия спиралей и вихрей разделяют полтора столетия. Спирали блистают как "надводная часть айсберга", поражая астрономов многообразием и динамичностью своих форм. Вихри оказались "подводной" частью того же "айсберга", обнаружить которую не могли многочисленные телескопы на самых различных длинах волн. И причина совсем не в недостаточной мощности телескопов, а в необходимости проведения самого этапа предсказания на уровне лабораторного и численного моделирования, аналитического исследования, в которых выявляется природа этих скрытых структур, место их локализации и способ их обнаружения по полученным данным наблюдения. Многолетние усилия по поиску этих структур позволяют теперь получить динамический портрет спиральных галактик, о чем мы не могли и мечтать в то время, когда только приступали к рассматриваемой здесь работе.

7. Предсказание и открытие гигантских циклонов

Как отмечалось в разделе 5 (рис. 7д и 8а), в системе отсчета, вращающейся со скоростью спиральных рукавов, направления вращения диска внутри и вне коротационной окружности противоположны (сплошные линии со стрелками на рис. 17а). Для двухрукавной галактики, представленной на рис. 17а, возмущенные скорости (штриховые линии со стрелками) меняют знак четыре раза при изменении азимутального угла на 2π. Сами по себе возмущенные скорости образуют четыре вихреобразные структуры — два циклона и два антициклона (рис. 17а). Однако за счет того, что направления возмущенных (в волне плотности) азимутальных скоростей совпадают с направлением вращения между спиральными рукавами и противоположны ему на рукавах, невозмущенное вращение поддерживает антициклонические вихри и подавляет циклоны. По этой причине между рукавами всегда формируются антициклонические вихри. На рукавах циклоны могут образоваться лишь при преобладании возмущенных скоростей, вращение же их только подавляет. Следовательно, условием существования циклонических вихрей в полном поле скоростей галактики оказывается преобладание градиента возмущенной азимутальной скорости над градиентом скорости вращения в системе координат, связанной со спиральным узором:

        (30)

Следует отметить, что в спиральной галактике в системе координат галактического центра возмущенные скорости всегда меньше скорости вращения, а в большинстве случаев даже много меньше. Тем не менее градиент возмущенной скорости может в некоторых областях диска превышать градиент скорости вращения вследствие различия в характерных масштабах изменения этих величин. Наличие таких областей в области коротационной окружности означает возможность появления в данной галактике циклонов в поле скоростей. Изложенные представления привели к предсказанию существования циклонов в галактиках с сильной спиральной структурой [39].

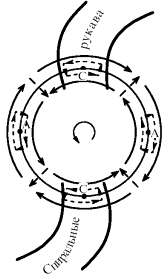
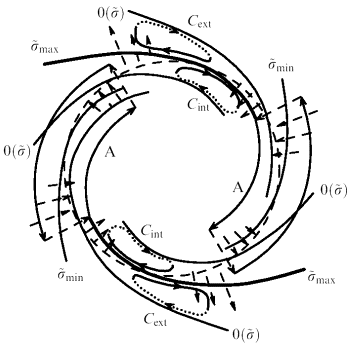
Рис. 17. (а) Схематическое представление стационарного (сплошные линии со стрелками) и возмущенного (штриховые линии со стрелками) полей скоростей в окрестности коротационной окружности в системе координат, вращающейся вместе со спиральным узором. (б) Поле скоростей в системе координат, вращающейся вместе со спиральным узором, в плоскости диска галактики с сильной волной плотности: помимо двух антициклонов, расположенных между спиральными рукавами, вихревая структура включает в себя две пары циклонов с центрами по разные стороны от коротационной окружности (штриховая окружность) и от линии максимумов поверхностной плотности (жирная кривая), (в) Амплитуда возмущенной азимутальной скорости C_φ (квадраты), вычисленная как функция радиуса, наложенная на профиль скорости вращения (крестики) в сопутствующей спиралям системе отсчета |v_circ| = |v_rot – Ω_ph r_c|, r_c ~ 42".

Можно показать, что возможны четыре различных варианта расположения циклонических вихрей. Три из них состоят в формировании пары циклонов с центрами на коротационной окружности, внутри нее либо вне нее. Четвертый вариант объединяет второй и третий -формируются четыре циклонических вихря по обе стороны от коротационной окружности. При этом циклоны оказываются слегка сдвинутыми относительно линии максимумов поверхностной плотности (рис. 17б) [41].

Теоретическое предсказание возможности существования циклонических вихрей в поле скоростей галактик с сильной спиральной структурой [39] подтвердилось, когда было восстановлено поле скоростей в плоскости диска галактики NGC 3631 [33, 41]. (Кажущееся противоречие — статья с предсказанием вышла позже статьи с открытием – связано с аномально долгим рецензированием первой из них.)

На рисунке 17в сравниваются радиальные зависимости возмущенной азимутальной скорости и скорости вращения диска NGC3631 в сопутствующей системе координат v_circ. Радиус коротации в этой галактике составляет около 42". Как видно из рис.17в условие (30) выполняется по обе стороны от коротационной окружности (наклон кривой, описывающей поведение v_φ, больше, чем кривой v_circ ). Следовательно, согласно предсказанию, мы вправе ожидать обнаружения циклонов по обе стороны от коротационной окружности так, как это изображено на рис. 17б.

Восстановленное поле скоростей газа в диске NGC3631 в системе координат, вращающейся вместе со спиральным узором, представлено на рис. 18а. Здесь мы видим структуру поля скоростей, включающую в себя два антициклона между спиральными рукавами и четыре циклона, расположение которых находится в полном согласии с предсказаниями теории (рис. 17б) [33, 41].

Рис. 18. (а) Восстановленное поле скоростей газа в системе координат, вращающейся вместе со спиральным узором, в диске галактики NGC3631, обладающей сильной волной плотности. Звездочками показано положение максимумов поверхностной яркости галактики в R-диапазоне (рис. 15а), расположение циклонических вихрей, открытых в этой галактике, совпадает с предсказываемым на основе теории волн плотности (рис. 176). (б, в) Эйнштейновская модель сферически симметричного звездного кластера: (б) все частицы движутся по круговым орбитам вокруг центра масс в направлении, указанном стрелками; (в) в плоскости, касательной к произвольной сфере в произвольной ее точке, сумма скоростей всех частиц равна нулю, (г) Схема превращения сферической бесстолкновительной системы в эллипсоидальную в результате развития неустойчивости радиальных орбит.

8. Существуют ли в спиральных галактиках медленные бары?

Из классической теории жидких фигур вращения хорошо известно, что если начать вращать гравитирующий шар из несжимаемой жидкости, то он превратится вначале в двухосный эллипсоид, а при более быстром вращении — в трехосный [42]. Отсюда мы делаем вывод о наличии связи между моментом вращения гравитирующего жидкого тела и его формой.

У бесстолкновительных звездных систем такая связь отсутствует. Это значит, что, с одной стороны, можно указать на сферическую систему с отличным от нуля моментом вращения, а с другой — на практически невращающиеся эллипсоиды, у которых отношение энергии вращения к гравитационной (потенциальной) энергии является малым параметром. Для эллиптических галактик такое отношение составляет примерно 13 %. Форма эллиптических галактик в основном определяется анизотропией их "температур" — отношение дисперсий скоростей вдоль и поперек оси вращения меньше единицы. Что же касается возможности вращения сферически симметричной звездной системы, то, как показал Линден-Белл [43], такая ситуация в принципе реализуема.

Это нетрудно понять, если учесть, что <...>

Как можно качественно представить себе формирование баров в галактиках? Согласно наблюдениям имеется довольно широкое распределение галактик по удельным моментам. Протогалактики, получившие сравнительно большой удельный момент, образовали массивные диски, в которых в результате так называемой бар-неустойчивости формируется большой "быстрый" бар. У концов бара, где начинаются отстающие спиральные рукава, их линейная скорость и линейная скорость дифференциально вращающегося диска совпадают (если бар жестко связан со спиралями). Эта область диска у концов бара является местом основного — коротационного — резонанса галактического диска. Такой бар называют быстрым в отличие от медленного бара, концы которого вращаются много медленнее примыкающей к ним области.

Медленный бар мог возникнуть в протогалактике с удельным моментом, меньшим, чем в той, в которой образовался быстрый бар. Образование медленного бара могло оказаться результатом неустойчивости радиальных орбит. Центральное уплотнение, образованное при радиальном коллапсе и в результате имеющее радиально вытянутые орбиты звезд, оказалось более "холодным" в трансверсальном направлении, чем в радиальном. В радиальные движения вкладывалась при коллапсе основная гравитационная энергия. Не удивительно поэтому, что радиальная дисперсия скоростей оказывается заметно больше трансверсальной. Малые возмущения в трансверсальном направлении начинают нарастать, чему не в силах противостоять малая транс-версальная дисперсия (рис. 18г). Фактически в трансверсальном направлении развивается анизотропная джинсовская неустойчивость, приводящая к нарастанию дисперсии в этом направлении и соответственно к уменьшению "эксцентриситета" звездных орбит (орбиты в общем случае не замкнуты).

Такая неустойчивость радиальных (или вытянутых) орбит была предсказана Зельдовичем с соавторами [47] в 1972 г. Неустойчивость радиальных орбит принадлежит к классу джинсовских неустойчивостей. Это означает, что в процессе такой неустойчивости наиболее быстро возрастает по амплитуде самая крупномасштабная коллективная мода колебаний, превращающая сферическую систему в двухосный эллипсоид (рис. 18г) [48]. Последний медленно вращается с частотой прецессии много меньшей характерной частоты обращения звезд (Ω_pr << Ω₀), отсюда и название — "медленный бар". Необходимое условие неустойчивости радиальных орбит: dΩ_pr/dL > 0, где L — момент звезды, в точности совпадает с условием возникновения медленного бара в результате захвата звезд гравитационным бар-потенциалом [49].

Согласно В.Л. Поляченко положение медленного бара должно обладать следующими особенностями:
1) его радиус ограничен внутренним-внутренним линдбладовским резонансом;
2) в случае медленного бара основные спиральные рукава галактики, являясь отстающими спиралями, ограничены со стороны центральной области внешним-внутренним линдбладовским резонансом;
3) концы медленного бара соединены с основными спиральными рукавами лидирующими спиралями азимутальной протяженностью ~180°.

На рисунке 19а показан отклик газового диска на гравитационный потенциал медленного бара, впервые вычисленный в [50]. Как мы видим, отклик состоит из двух спиралей. Первая представляет собой часть отстающей спирали (внешней), являющейся продолжением основных отстающих спиральных рукавов галактики. Вторая спираль оказывается лидирующей. Занимая узкий в радиальном направлении участок диска, последняя является очень туго закрученной и делает полоборота между баром и внешней спиралью. Лидирующая спираль локализована между внутренним-внутренним (IILR) (концы бара) и внешним-внутренним (OILR) (начало отстающей спирали) линдбладовскими резонан-сами.

Рис. 19. (а) Отклик газового диска на гравитационный потенциал медленного бара [50]. (б) Положения максимумов второй фурье-гармоники широкополосного оптического изображения (х) и изображения в ближней ИК-полосе Н (ཾ), наложенные на оптическое изображение центральной части галактики NGC 157 [51]. Галактика вращается против часовой стрелки; это означает, что от концов бара начинается лидирующая спираль, которая делает пол-оборота и затем переходит во внешнюю отстающую спираль, составляющую основной спиральный узор этой галактики Отчетливо видно качественное согласие структур бар-спирали на рис. а и б.

Именно такая форма спиральных рукавов в окрестности внутреннего линдбладовского резонанса галактики NGC 157 была нами обнаружена [51] в процессе анализа фотометрических данных по этой галактике, полученных с помощью Космического телескопа им. Хаббла (данные доступны благодаря существованию архива Космического телескопа им. Хаббла). На рисунке 19б показано положение максимума второй гармоники карты поверхностной яркости центральной части галактики NGC157, полученной в видимом диапазоне (центральная длина волны ~5852 ангстрем, ширина фильтра ~1873 ангстрем), в зависимости от радиуса. Бар протяженностью 10" отчетливо виден при наложении на рисунок второй гармоники карты яркости, полученной в ближней инфракрасной (ИК) полосе Н. Резонанс IILR как раз приходится на значение 5", OILR — на 8", лидирующие спирали соединяют концы бара на 5" с началом отстающей спирали, находящимся на 10", в 2" от OILR.

Таким образом, совпадение с теоретическим предсказанием оказалось очень хорошим, что является серьезным аргументом в пользу существования медленного бара в галактике NGC 157.

9. Наблюдаемая осцилляторная структура типа солитона огибающей в спиральном рукаве галактики NGC 1365.

Основная масса межзвездного газа в галактиках приходится на нейтральный водород, поэтому наиболее прямым способом измерения поля скоростей газового диска являются наблюдения в линии HI 21 см. Однако на сегодня угловое разрешение радионаблюдений, которое может быть достигнуто на большом поле, существенно уступает разрешению наблюдений в оптическом диапазоне. Именно по этой причине практически все подробно изученные поля скоростей спиральных галактик (за исключением самых близких) получены на основе измерения лучевых скоростей в линии Нα.

Особое положение среди радиоданных занимают наблюдения галактики NGC1365. Эта гигантская, близко расположенная к нам галактика обладает мощной спиральной структурой. Поэтому разрешение в линии 21 см оказывается достаточным для исследования внутренней детальной структуры спиральных рукавов в газовом диске галактики.

Как показывают наблюдения, нейтральный водород (HI) концентрируется в спиральных рукавах. Обладая показателем объемной адиабаты γ = 5/3, атомарный газ может иметь плотность во фронте "классической" сильной ударной волны в четыре раза превосходящую плотность перед фронтом, поскольку максимальное отношение плотностей равно (γ + 1)/(γ – 1). Однако наблюдения показывают, что это отношение может быть почти на порядок больше. Дополнительное сжатие газа по сравнению с ожидаемым в "классической" ударной волне вызывается сильным охлаждением газа за счет излучения (свободно-свободные переходы). Нас, однако, сейчас интересуют структуры, масштаб которых существенно превосходит ширину ударного фронта спиральной волны плотности в атомарном газе.

Поднимаемый вопрос о структурах в атомарном газе спиральных рукавов тесно связан с другим, имеющим четвертьвековую историю вопросом о том, что газовые диски галактик находятся (по набору своих основных параметров) вблизи границы их динамической неустойчивости. Такое положение представляется естественным: по мере развития неустойчивости возрастает дисперсия скоростей, диск "греется" и становится все более и более устойчивым до тех пор, пока не исчезает сама причина нагрева — диск выходит на границу устойчивости. Исследования [52], как и более поздние, подтвердили это предположение на примере различных выборок спиральных галактик.

Михайловский, Петвиашвили и Фридман [31, 32] показали, что нелинейная динамика газового галактического диска на границе гравитационной неустойчивости описывается нелинейным уравнением Шрёдингера. Это позволило высказать гипотезу, что спиральные рукава галактик являются солитонами огибающей (последние описываются одним из решений нелинейного уравнения Шрёдингера) (рис. 20а). Представление о спиральных рукавах, сохраняющих свою форму в дифференциально вращающемся галактическом диске, как о солитоне, который обладает свойством неизменности при распространении в неоднородных потоках и средах по определению, выглядит весьма естественным и привлекательным.

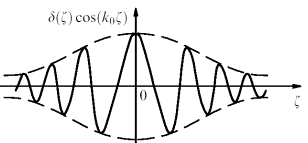
Рис. 20. (а) Предсказываемая теорией структура спиральных рукавов как солитона огибающей [31, 32], ζ — волновая переменная, характеризующая первичную волну, δ — функция, определяющая форму солитона огибающей, (б) Азимутальное распределение интенсивности радиоизлучения I в линии 21 см от спиральной галактики NGC 1365 на разных расстояниях r от центра галактики.

На рисунке 20б можно видеть, что реальные спиральные рукава в газовом диске галактики NGC 1365 действительно содержат осцилляторную структуру — крупномасштабная огибающая описывает два спиральных рукава, внутри каждого из которых имеется наполнение из мелкомасштабных квазипериодических вариаций плотности. Такая структура хорошо согласуется с предсказываемой теорией структурой солитона огибающей (рис. 20а).

Отметим, что в принципе сходное наблюдательное проявление могла бы иметь и вторичная гравитационная неустойчивость, генерирующая более коротковолновые вторичные возмущения в газе, "поджатом" в результате развития первичной неустойчивости.

10. Заключение

Кратко перечислим основные результаты, рассмотренные в обзоре.

• На установке, сконструированной в Курчатовском институте, при моделировании развития центробежной неустойчивости в газовых дисках галактик со скачком скорости вращения были обнаружены антициклонические вихри, центры которых располагались между спиральными рукавами в области скачка скорости. Это послужило основой для предсказания наличия таких структур в реальных галактиках с регулярной спиральной структурой, имеющих скачок скорости вращения.

• В газовом диске спиральной галактики Mrk 1040, имеющей большой скачок скорости вращения, были открыты антициклоны, расположение которых полностью согласовывалось с результатами эксперимента на вращающейся мелкой воде — центры антициклонов располагались между спиральными рукавами в области скачка скорости вращения.

• В солнечной окрестности газового диска нашей Галактики в области понижения скорости вращения были найдены антициклоны протяженностью « 4 кпк. Их происхождение естественно связать со спиральной структурой нашей Галактики, учитывая аргументы в пользу расположения орбиты Солнца вокруг центра Галактики около коротационной окружности.

• Теория предсказывает одновременное возникновение спиральных рукавов и вихрей в спиральной волне плотности независимо от механизма возбуждения: гидродинамической неустойчивости в присутствии скачка скорости вращения либо гравитационной неустойчивости в отсутствие каких бы то ни было резких градиентов параметров диска. В согласии с предсказаниями теории гигантские антициклоны были открыты в галактиках с регулярной спиральной структурой и гладкой кривой вращения: NGC157, NGC3631, NGC1365, NGC6148. Во всех случаях антициклоны располагаются между спиральными рукавами вблизи от коротационной окружности — именно там, где и предсказывает теория.

• В галактиках со спиральной волной плотности, имеющей большую амплитуду, теория предсказывает наличие не только антициклонов, но и циклонов, центры которых должны располагаться в максимуме поверхностной плотности на спиральных рукавах и на коротационной окружности либо по разные стороны от коротационной окружности и линии максимумов плотности спиральных рукавов. Гигантские циклоны были открыты в спиральной галактике NGC3631, обладающей регулярной спиральной структурой с большой амплитудой. Локализация циклонов полностью согласуется с предсказаниями теории.

• В спиральной галактике NGC157 был открыт медленный бар. Это положило конец более чем четвертьвековой дискуссии о возможности существования медленных баров в галактиках. Между концами бара и основной системой отстающих спиральных рукавов галактики располагается туго закрученная лидирующая спираль, делающая пол-оборота в узкой радиальной области диска между внутренним-внутренним и внешним-внутренним линдбладовскими резонансами. Именно такая нетривиальная структура была предсказана ранее как форма отклика галактического диска на потенциал медленного (и только медленного) бара, что однозначно указывает на его наличие в центре NGC 157.

• Внутренняя осцилляторная структура спиральных рукавов в газовом диске галактики NGC1365, недавно открытая по данным в линии 21 см о распределении нейтрального водорода в этой галактике, имеет форму солитона огибающей. Представление о спиральных волнах плотности как о солитонах огибающей было выдвинуто в работах с участием автора около четверти века назад.

• Открытие предсказанных ранее галактических структур потребовало существенного развития наблюдательной базы и новых методов обработки данных наблюдений.

• Разработан метод восстановления полного векторного поля скоростей газа в диске галактик с регулярной спиральной структурой из наблюдаемого однокомпо-нентного поля лучевой скорости. Метод предназначен для решения некорректной задачи, и поэтому принципиально важным является то, что он включает в себя несколько независимых наблюдательных тестов для проверки корректности используемых модельных представлений.

• Разработан наблюдательный тест для проверки волновой природы спиральной структуры, наблюдаемой в конкретной спиральной галактике.

• Разработан наблюдательный тест для проверки природы вертикальных движений в дисковых галактиках, с помощью которого можно выяснить, являются ли они следствием изгибных колебаний или г-компонентой поля скоростей волны плотности.

Все перечисленные результаты являются пионерскими и не имеют аналогов за рубежом.

Список литературы

1. Афанасьев В.Л. и др. Астрофизика 28 243; 29 155 (1988); Астрон. журн. 68 1134 (1991); 69 19 (1992)
2. Баев П. В., Маков Ю. Н., Фридман А. М. Письма в Астрон. журн. 13 964 (1987); Баев П. В., Фридман А. М. Астрон. цирк. (1535) 1 (1989)
3. Фридман А. М. УФН 125 352 (1978)
4. Lindblad В. Stockholms Observat. Ann. 29 155 (1941); Lin С С, Shu F H Astrophys. J. 140 646 (1964); Proc. Natl. Acad. Sei. USA 55 229 (1966)
5. Ландау Л. Д., Лифшиц Е. М. Гидродинамика (М.: Наука, 1988) §108
6. Фридман А. М. ЖЭТФ 98 1121 (1990)
7. Fridman А. М. "Theory of gradient instabilities of a gaseous galactic disc and rotating shallow water", in Dynamics ofAstrophysicalDiscs (Ed. J A Seilwood) (Cambridge: Cambridge Univ. Press, 1989) p. 185
8. Морозов А. Г. и др. Письма в ЖЭТФ 39 504 (1984); УФН 145 161 (1985); Fridman А. М. et al. Phys. Leu. А 109 228 (1985)
9. Незлин М. В. и др. Письма в Астрон. журн. 12 504 (1986)
10. Jeans J H Astronomy and Cosmogony 2nd ed. (Cambridge: The Univ. Press, 1929)
11. Fridman A M et al. Astrophys. Space Sei. 252 115 (1997)
12. Ляхович В В и др. Астрон. журн. 74 509 (1997)
13. Морозов А Г Астрон. журн. 56 498 (1979)
14. Combes F. Annu. Rev. Astron. Astrophys. 29 195 (1991)
15. Сумин А. А., Фридман А. М., Хауд У. А. Письма в Астрон. журн. 17 698, 779 (1991)
16. Горькавый Н. Н., Фридман А. М. Физика планетных колец: Небесная механика сплошной среды (М.: Наука, 1994)
17. Ландау Л. Д. ДАН СССР 44 151 (1944)
18. Лойцянский Л. Г. Механика жидкости и газа 4-е изд. (М.: Наука, 1973)
19. Фридман А. М. УФН 160 179 (1990)
20. Незлин М. В., Снежкин Е. Н. Вихри и спиральные структуры. Астрофизика и физика плазмы в опытах на мелкой воде (М.: Наука, 1990)
21. Паша И. И. Письма в Астрон. журн. 11 3 (1985)
22. Афанасьев В. Л., Фридман А. М. Письма в Астрон. журн. 19 787 (1993)
23. Ефремов Ю. Н. Письма в Астрон. журн. 9 94 (1983)
24. Аведисова В. С. Астрофизика 30 140 (1989)
25. Mishurov Yu N. et al. Astron. Astrophys. 323 775 (1997)
26. Fridman A. M. "Dynamics of disks in the Milky Way: some solved Problems and some puzzles", in Physics of the Gaseous and Stellar Disks of the Galaxy (Astron. Soc. of the Pacific Conf. Ser., Vol. 66, Ed. IR King) (San Francisco: Astron. Soc.of the Pacific, 1994) p. 15
27. Fridman А. М. et al., in UnsolvedProblems ofthe Milky Way. Proc. of the 169th Symp. ofthe Intern. Union, The Hague, The Netherlands, August 23-29, 1994 (Eds L Blitz, P. Teuben) (Dordrecht: Kluwer Acad. Publ., 1996) p. 597
28. Ляхович В. В., Фридман А. М., Хоружий О. В. Астрон. журн. 73 24 (1996)
29. Ляхович В. В., Фридман А. М., Хоружий О. В., в сб. Неустойчивые процессы во Вселенной (Отв. ред. А. Г. Масевич) (М.: Космосинформ, 1994) с. 194
30. Contopoulos G. Astron. Astrophys. 64 323 (1978)
31. Михайловский А. Б., Петвиашвили В. И., Фридман А. М. Письма в ЖЭТФ 26 129 (1977)
32. Михайловский А. Б., Петвиашвили В. И., Фридман А. М. Астрон. журн. 56 279 (1979)
33. Fridman А. М. et al. "Gas motions in the plan of the spiral galaxy NGC 3631", Mon. Not. R. Astron. Soc. 323 651 (2001)
34. Фридман А. М. и др. Письма в Астрон. журн. 24 883 (1998)
35. Fridman А. М., Polyachenko V. L. Physics of Gravitating Systems Vols 1, 2 (New York: Springer-Verlag, 1984)
36. Knapen J.H. "Atomic hydrogen in the spiral galaxy NGC 3631", Mon. Not. R. Astron. Soc. 286 403 (1997)
37. Fridman A.M. et al. "Investigation of the dynamicsof spiral galaxies on the base of 3D vector velocity field of their gaseous disks reconstructed from observed line-of-sight velocity field", in The Combination of Theory, Observation, and Simulation for the Dynamics of Stars and Star Clusters in the Galaxy, 23rd Meeting of the IAU, Joint Discussion 15,25 August 1997, Kyoto, Japan, Meeting Abstracts (Ed. J Andersen) (Dordrecht: Kluwer Acad. Publ., 1998) p. 39
38. Fridman А. М. et al. "Discovery of new structures — giant antycyclones — in disks of spiral galaxies", in Searchingfor Absolute Values and Unity in the Sciences: Science for the Benefit of Humanity: Commemorative Volume ofthe Twenty-first Intern. Conf. on the Unit ofthe Sciences, 1997 (Lexington, Ky.: ICCU, 1997)
39. Fridman А. М. et al. Astron. Astrophys. 371 538 (2001)
40. Fridman A. M. et al. "New structures in galactic disks: predictions and discoveries", in Galaxy Disks andDisk Galaxies (Astron. Soc. of the Pacific Conf. Ser., Vol. 230, Eds J G Funes, E M Corsini) (San Francisco, Calif: Astron. Soc. ofthe Pacific, 2001) p. 187
41. Fridman A. M. et al. Phys. Lett. А 264 85 (1999)
42. Chandrasekhar S Ellipsoidal Figures of Equilibrium (New Haven: Yale Univ. Press, 1969)
43. Lynden-Bell D. "Can spherical Clusters rotate?" Mon. Not. R. Astron.Soc. 120 204 (1960)
44. Михайловский А. В., Фридман А. М., Эпельбаум Я. Г. ЖЭТФ 59 1608 (1970)
45. Сынах В. С., Фридман А. М., Шухман И. Г. ДАН СССР 201 827 (1971)
46. Фридман А. М., Шухман И. Г. ДАН СССР 202 67 (1972)
47. Зельдович Я. Б. и др., Препринт № 7-72 (Иркутск: ИЗМИРАН, 1972)
48. Поляченко В. Л. Письма в Астрой, журн. 7 (3) 142 (1981)
49. Lynden-Bell D. Mon. Not. R. Astron. Soc. 187 101 (1979)
50. Polyachenko V. L., in Physics ofthe Gaseous and Stellar Disks of the Galaxy (Astron. Soc. ofthe Pacific Conf. Ser., Vol. 66, Ed. IR King) (San Francisco, Calif: Astron. Soc. ofthe Pacific, 1994) p. 103
51. Fridman A. M., Khoruzhii О. V. Phys. Lett. А 276 199 (2000)
52. Засов А. В., Симаков С. Г. Астрофизика 29 190 (1988)

©  А.М. Фридман
Институт астрономии РАН,
119017 Москва, ул. Пятницкая 48, Российская Федерация
Тел. (495) 951-79-93. Факс (495) 230-20-81
E-mail: afridman@inasan.rssi.ru
Российский научный центр "Курчатовский институт",
Институт физики стохастических структур,
123182 Москва, пл. Курчатова 1, Российская Федерация
Статья поступила 7 сентября 2006 г., после доработки 2 октября 2006 г.