Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
1.3. Методы доказательства в логике Буля
Практические задания по логике Буля
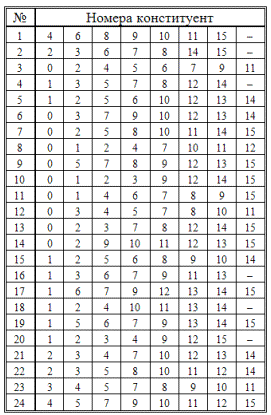
1. В табл. 1.20 заданы номера наборов аргументов, на которых логическая функция принимает значение, равное единице. Необходимо записать эту функцию в СДНФ и произвести ее минимизацию методом Куайна, методом сочетания индексов и методом Карно (результаты минимизации для всех трех случаев должны совпасть).
Таблица 1.20
2. Логическую функцию вашего варианта из предыдущего задания (табл. 1.20) запишите в СКНФ. Как нужно модифицировать метод Куайна, метод сочетания индексов и метод Карно, чтобы приспособить их к СКНФ? Произведите минимизацию вашей функции, записанной в СКНФ, всеми тремя методами (три результата этого пункта должны совпадать между собой и с тремя результатами предыдущего пункта).
3. Ниже приведены логические выражения. Максимально упростите выражение своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
1. (а ∨ (d ∧ b)) ∧ ((а ∧ (b ∨ d)) ∨ c)) ∨ c ∨ (а ∨ (b ∧ d)),
2. ((а ∨ c) ∧ (а ∨ d)) ∧ (((c ∨ (c ∧ b)) ∧ c) ∨ а),
3. (b ∨ d) ∧ ((d ∧ c) ∨ (а ∧ c) ∨ (d ∧ c) ∨ (а ∧ c)) ∧ (b ∨ d),
4. (а ∨ c) ∧ (а ∨ b) ∧ (b ∨ c) ∧ (а ∨ b) ∧ (b ∨ c),
5. (а ∧ c) ∨ ((b ∨ d) ∧ (а ∨ d) ∧ (d ∨ b) ∧ (а ∨ d)) ∨ (а ∧ c),
6. ((b ∨ c) ∧ (а ∨ b)) ∨ (d ∧ c) ∨ (((b ∧ а) ∨ c) ∧ (а ∨ b)),
7. (а ∧ c) ∨ (а ∧ b) ∨ (b ∧ c) ∨ (а ∧ b) ∨ (c ∧ b),
8. ((а ∨ (c ∨ (b ∧ c))) ∧ (c ∧ d) ∧ (c ∧ d)) ∧ (c ∨ (d ∧ c) ∨ d),
9. ((а ∨ а) ∧ (b ∨ d) ∧ (b ∨ c) ∧ (c ∨ d)) ∨ ((b ∨ c) ∧ (c ∨ d)),
10. (а ∨ c) ∧ ((а ∧ d) ∨ (b ∧ d) ∨ (а ∧ d) ∨ (b ∧ d)) ∧ (а ∨ c),
11. ((d ∧ c) ∨ (d ∧ b) ∨ (c ∧ b)) ∧ ((d ∧ b) ∨ (c ∧ b)) ∧ (а ∨ а),
12. ((c ∧ d) ∨ (b ∧ c)) ∧ (а ∨ d) ∧ (((c ∨ b) ∧ d) ∨(c ∧ b)),
13. ((а ∨ b) ∧ (b ∧ c ∧ d) ∨ (а ∧ b ∧ c ∧ d) ∨ b ∨ c ∨ d,
14. ((а ∧ b) ∨ (а ∧ b)) ∨ ((а ∨ b) ∧ (c ∨ d) ∧ (а ∨ b) ∧ (d ∨ c)),
15. ((b ∧ c) ∨ (c ∨ d) ∨ а) ∧ (а ∨ b ∨ c ∨ d) ∧ (c ∨ d) ∧ а,
16. ((b ∨ c) ∧ (d ∨ (b ∧ c))) ∨ (d ∧ а) ∨ ((c ∨ b) ∧ (d ∨ c)),
17. (b ∧ d) ∨ ((c ∨ d) ∧ (а ∨ c) ∧ (d ∨ c) ∧ (а ∨ c)) ∨ (b ∧ d),
18. ((c ∨ d) ∧ (d ∨ а)) ∨ ((b ∨ b) ∧ (c ∨ а) ∧ (c ∨ d) ∧ (d ∨ а)),
19. (а ∧ d) ∨ (((c ∧ b) ∨ d) ∧ (c ∨ b)) ∨ ((d ∨ c) ∧ (c ∨ b)),
20. (((d ∨ (d ∧ c)) ∧ d) ∨ b) ∧ ((b ∨ d) ∧ (b ∨ а)),
21. ((b ∧ (c ∨ а)) ∨ d)) ∨ d ∨ (b ∨ (c ∧ а)) ∧ (b ∨ (а ∧ c)),
22. ((c ∨ а) ∧ (а ∨ b) ∧ (а ∨ c) ∧ (b ∨ а)) ∨ (b ∧ d) ∨ (b ∧ d),
23. (d ∨ (а ∧ d) ∨ а) ∧ ((b ∨ (d ∨ (d ∧ c))) ∧ (c ∧ а) ∧ ( d ∧ а)),
24. (c ∧ b) ∨ (d ∧ c) ∨ (b ∧ c) ∨ (d ∧ c) ∨ (b ∧ d).
4. Аналитическим способом, т.е. на основе формул взаимосвязи между логическими операциями, докажите справедливость ниже приведенных тождеств. Затем с помощью диаграмм Эйлера — Венна подтвердите справедливость этого доказательства. Представьте одно из выражений (предварительно его упростив) в базисе элементарных функций. В наборе номеров базисных функций должны фигурировать цифры вашего варианта. Например, для варианта 12 могут быть взяты следующие функции: f1, f2, f12. Недостающие функции отбираются на основе теории классов.
1. ((а | b) | (а ~ b)) | ((c + d) → (d – c)) =
= ((b → c) → (а – c)) ↓ ((а | d) | (d → b)),
2. ((а ∧ c) ↓ (b – c)) ∧ ((а | d) – (b ∧ d)) =
= ((а | b) | (а + b)) → ((c + d) ∧ (d → c)),
3. ((а ↓ b) ∨ (а + b)) – ((c – d) ↓ (c ~ d)) =
= ((c → а) ∧ (c → b)) → ((а ↓ d) ∨ (b ↓ d)),
4. ((а ~ b) – (а ↓ b)) ↓ ((c ~ d) ↓ (c – d)) =
= ((c – а) ↓ (c – b)) | ((а ↓ d) ↓ (b ↓ d)),
5. ((а ∧ b) ∨ (а + b)) – ((d – c) ↓ (d ~ c)) =
= ((а → c) ∧ (b → c)) → ((а | d) | (b | d)),
6. ((а ∨ b) – (а + b)) ∨ ((c – d) ↓ (c ~ d)) =
= ((c – а) ↓ (c – b)) ∧ ((а ∨ d) – (b ↓ d)),
7. ((d → b) → (c – b)) ↓ ((c ∨ а) | (d → а)) =
= ((c | d) | (c + d)) | ((а ~ b) → (а – b)),
8. ((а | b) – (а + b)) ∨ ((d – c) ↓ (c ~ d)) =
= ((а ↓ d) ↓ (b – d)) ∧ ((а → c) – (b – c)),
9. ((c – а) ∨ (c ~ а)) – ((d – b) ↓ (d ~ b)) =
= ((а ∨ b) ∧ (c → b)) → ((d – а) ∨ (c ∧ d)),
10. ((c ~ b) – (b ↓ c)) ↓ ((а ~ d) ↓ (а – d)) =
= ((b ↓ d) ↓ (c ↓ d)) | ((а – b) ↓ (а – c)),
11. ((а – d) ∨ (а ~ d)) – ((b – c) ↓ (b ~ c)) =
= ((b → d) ∧ (а | b)) → ((c ∨ d) | (а → c)),
12. ((b ↓ d) ↓ (c ↓ d)) ∧ ((а → b) – (а – c)) =
= ((b ∨ c) – (b + c)) ∨ ((а – d) ↓ (а ~ d)),
13. ((c → d) | (c + d)) | ((а ~ b) → (а ∧ b)) =
= ((а → c) → (а – d)) ↓ ((b → d) | (b → c)),
14. ((b ∧ d) ↓ (b ∧ c)) ∧ ((d → а) – (c – а)) =
= ((c | d) | (c ~ d)) → ((а + b) ∧ (b → а)),
15. ((d – а) ∨ (d ~ а)) – ((c – b) ↓ (c + b)) =
= ((а ∨ b) ∧ (d → b)) → ((c ∧ d) ∨ (c – а)),
16. ((c → d) – (c ~ d)) ∨ ((а ∧ b) ↓ (а + b)) =
= ((b ∧ c) ↓ (b – d)) ∧ ((а | c) – (а – d)),
17. ((c → b) → (d ↓ b)) ↓ ((а → d) | (а → c)) =
= ((c ∨ d) | (c ~ d)) | ((а + b) → (а – b)),
18. ((а ∧ c) ↓ (b – а)) ∧ ((c → d) – (b – d)) =
= ((b | c) | (b ~ c)) → ((а + d) ∧ (а → d)),
19. ((b ↓ d) ∨ (b + d)) – ((а – c) ↓ (а ~ c)) =
= ((c → b) ∧ (d → c)) → ((а – b) ∨ (а ∧ d)),
20. ((d ∧ а) ↓ (b ∧ d)) | ((а – c) ↓ (b – c)) =
= ((а + b) – (b ∧ а)) ↓ ((c ~ d) ↓ (d – c)),
21. ((а ↓ b) ∨ (а ~ b)) – ((c – d) ↓ (c ~ d)) =
= ((а → d) ∧ (d → b)) → ((c → а) | (c → b)),
22. ((c → а) – (а + c)) ∨ ((d – b) ↓ (b ~ d)) =
= ((а ↓ b) ↓ (c – b)) ∧ ((d → а) – (c ∧ d)),
23. ((с | b) | (с ~ b)) | ((а + d) → (а – d)) =
= ((c → d) → (b – d)) ↓ ((b | а) | (а → c)),
24. ((c ↓ b) ∨ (c + b)) – ((d – а) ↓ (d ~ а)) =
= ((d → b) ∧ (d → c)) → ((b ↓ а) ∨ (c ↓ а)).
5. Воспользовавшись таблицами истинности, представьте логические выражения вашего варианта двух последних заданий в СПНФ. Затем произведите минимизацию (результаты расчета проверьте с помощью таблиц истинности). Наконец, определите, к каким классам (0, 1, 2, 3 или 4) относятся ваши логические выражения.
6. Докажите аналитическим путем справедливость выражений.
Вариант 1.
(A – B) + (C – D) = A + C, если A ∩ B = C ∩ D;
A ∪ B ∪ (A ∩ B ∩ C) ∪ (A ∩ B ∩ C) = 1;
(а ~ b) – (а | b) = а ∧ b.
Вариант 2.
(A – B) + (B – C) + (B – A) + (C – B) = A + C;
((A ∪ B) ∩ (B ∪ C)) ∪ ((A ∪ B) ∩ (B ∪ C)) = 1;
а → b = (а + b) ~ (b – а).
Вариант 3.
(A – B) + (B – C) + (C – A) = (B – A) + (C – B) + (A – C);
((A ∪ B) – C) ⊂ (A ∪ (B – C));
((а ↓ b) ↓ (а ↓ b)) + ((а ↓ а) ↓ (b ↓ b)) = а + b.
Вариант 4.
(A ∪ B) + (C ∪ D) = B + C, если A ∩ B = D, C ∩ D = A;
((B ∩ C) ∪ (A ∩ C)) ∩ ((B ∩ C) ∪ (A ∩ C)) = 0;
а → c = (а ∨ (b ∧ c)) → (а ∨ b) ∧ c).
Вариант 5.
(A – (B – C)) – ((A – B) – C) = A ∩ C;
((A ∪ B) ∩ (B ∪ C)) ∪ ((A ∪ B) ∩ (B ∪ C)) = 1;
(b ∨ (c ∧ а)) ∨ (а ∨ (b ∧ c)) = а ∨ b.
Вариант 6.
(A ∩ B ∩ C) ∪ (A ∩ B) ∪ (A ∩ C) = A;
A ∩ B = A, если A ∪ B = 1;
(а | (b | c)) + (b | (а | c)) + (c | (а | b)) =
= (а → (b ∨ c)) ∧ (b → (а ∨ c)) ∧ (c → (а ∨ b)).
Вариант 7.
(A ∪ B) + (A ∪ C) + (B ∪ C) = (A ∩ B) + (A ∩ C) + (B ∩ C);
((A ∪ B) – C) ⊂ ((A – C) ∪ (B – A));
((а ↓ b) ∨ (а | b)) → ((а ∧ b) | (а + b)) = 1.
Вариант 8.
((A ∪ B) ∩ C) ∪ (A ∩ (B ∪ C)) = A ∪ C;
(A – (B – C)) ⊂ ((A – B) ∪ (B ∩ C));
а ↓ ((b – а) ~ b) = 0.
Вариант 9.
(A ∩ B) – (C ∪ D) = (A – C) ∩ (B – D);
(A ∩ (B ∪ C)) ⊂ ((A ∩ B) ∪ C);
а ~ (b | c) = ((а + b) ∧ c) + (а – c).
Вариант 10.
(A – B) + (B – A) = A + B;
P – Q = A ∩ C, если P = A – (B – C), Q = (A – B) – C;
(а ~ b) – (а | b) = (а ↓ а) ↓ (b ↓ b).
Вариант 11.
((A ∩ B) ∪ (B ∩ C)) ∩ ((A ∩ B) ∪ (B ∩ C)) = 0;
(A – (B – C)) ⊂ (A ∪ (B ∩ C));
(b ∨ (а ∧ c)) → (b ∨ c) ∧ а) = b → a.
Вариант 12.
(A ∪ B) + (C ∪ D) = A + B + C + D, если A ∩ B = C ∩ D;
(A – B) – C = (A – C) – (B – C);
(а ∧ (b ∧ c) ∨ ((а ∨ c) ∧ b) = а ∨ b.
Вариант 13.
((A ∩ C) + (B ∩ D)) ⊂ ((A + B) ∪ (C + D));
(A + B) – C) = (A – (B ∪ C)) ∪ (B – (A ∪ C));
(а | b) → (b ∨ c) = b ∨ c.
Вариант 14.
((B ∩ C) ∪ (A ∩ B) ∪ (A ∩ C)) ∩ ((A ∩ B) ∪ (B ∩ C)) = 0;
(A – B) ∪ (B – A) = (B – A) + (A – B);
(а ↓ b) + (b ↓ c) = (а + c) – b.
Вариант 15.
P = (A – B) – C, Q = A – (B – C), если P ⊂ Q;
(A – B) ∪ (B – C) ∪ (C – A) = (A ∪ B ∪ C) + (A ∩ B ∩ C);
(а ∨ b ∨ c) ~ (а ∧ b ∧ c) = (а → b) ∧ (b → c) ∧ (c → а).
Вариант 16.
((A ∪ C) + (B ∪ D)) ⊂ ((A + B) ∪ (C + D));
((B ∩ A) ∪ C) ∩ ((A ∪ C) ∪ B) = B ∩ C;
((а + b) – c) | ((а – b) + c) = а → (b ∨ c).
Вариант 17.
(C ∩ B) ∪ (B ∩ A) ∪ (B ∩ C) ∪ (A ∩ B) ∪ (A ∩ C) = 1;
(A ∩ B) ∪ C = A ∩ (B ∪ C), если C ⊂ A;
(а ~ b) ↓ ((а ↓ c) → (c ∧ d)) = (b – а) – c.
Вариант 18.
A – (B ∪ C) = (A – B) ∩ (A – C);
P ⊂ Q, если P = (A – B) – C, Q = A – (B – C);
((а | b) → (b ∨ c)) ↓ (c ~ d) = (d – c) – b.
Вариант 19.
(A – (B ∪ C)) ∪ (B – (A ∪ C)) ∪ (C – (A ∪ B)) =
= A + B + C + (A ∩ B ∩ C);
((A ∪ B) – C) ⊂ ((A ∪ B ∪ C) – (A ∩ B ∩ C));
(а – b) – c = (а ~ b) ↓ (b ∨ c).
Вариант 20.
A + B = (A ∪ B) + (A ∪ B);
(A ∩ B) ∪ (B ∩ C) ∪ (A ∩ C) = (A ∪ B) ∩ (B ∪ C) ∩ (A ∪ C);
(а – b) + (а + c) ∧ b = а + (b | c).
Вариант 21.
(A ∪ B) + (B ∪ A) = (A ∩ B) + (A ∪ B);
(A ∪ B) ∩ (B ∪ C) ⊂ (A ∪ C);
а + (c – b) = (а ~ c) + (b | c).
Вариант 22.
A + B = (A – B) + (B – A);
C ∪ (A ∪ B), если C ∪ A, C ∪ B;
(а ↓ b) ↓ ((а | c) ↓ (b | d)) = а ∨ b.
Вариант 23.
(A – B) + ((A + C) ∩ B) = (A – C) + ((A + B) ∩ C);
(A ∪ B) ∩ C = A ∪ (B ∩ C), если A ⊂ C;
((а | b) → (b ∨ c)) ∨ (c ~ d) = d → (c ∨ b).
Вариант 24.
(A + (A – B)) ∩ (1 – B) = 0;
((A – C) ∪ (B – A)) ⊂ (A ∪ B);
а ~ (b | c) = (а → b) ~ (а + c) ∧ b.
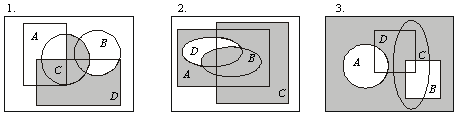
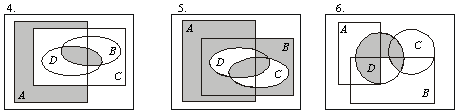
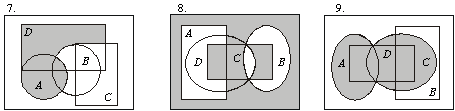
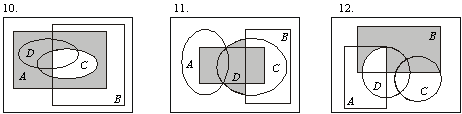
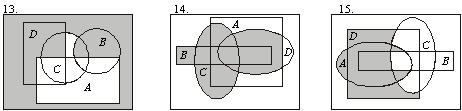
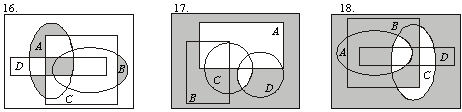
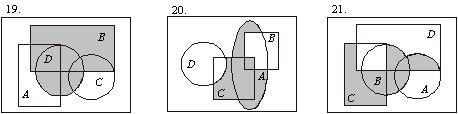
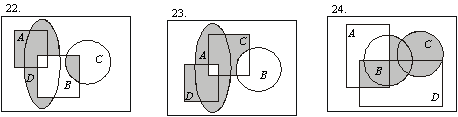
7. Ниже приведены диаграммы Эйлера – Венна. Представьте заштрихованные и отдельно не заштрихованные области максимально компактными аналитическими выражениями, в которых бы использовалось минимальное количество логических операций и букв. С этой целью сначала выразите все заштрихованные области через конституенты-конъюнкты, а незаштрихованные — через конституенты-дизъюнкты, и только после этого приступайте к упрощению совершенных форм (результаты проверьте на таблицах истинности).