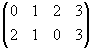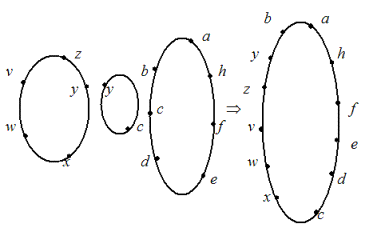Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.1. Группа и связанные с ней понятия

Циклическая форма подстановок

Подстановки удобно записывать в циклической форме. При такой записи индексы, остающиеся на месте, обычно не пишутся. Так, подстановка a имеет следующие переходы индексов: 0 → 0, 1 → 4 → 2 → 1, 3 → 3, 5 → 6 → 5. Следовательно, в циклической форме она запишется следующим образом:

а = = (0)(142)(3)(56) =

= (0)(142)(3)(56)(7)(8)... = (142)(56).

Считается, что индексы 7, 8 и т.д. так же, как 0 и 3, неявно присутствуют в подстановке а, но тождественно переходят сами в себя. В связи с этим тождественную подстановку обозначают через единичный цикл: e = (0). Регулярные подстановки группы G имеют следующий циклический вид:

0 = (0),     1 = (01)(23)(45)(67),

2 = (02)(13)(46)(57),     3 = (03)(12)(47)(56),

4 = (0426)(1537),     5 = (0527)(1436),

6 = (0624)(1735),     7 = (0725)(1634).

Безразлично, с какой позиции записывать цикл:

(ij) = (ji),     (ijk) = (jki) = (kij),     (ijkl) = (jkli) = ... ,

поэтому

i₁ = (0123) = (1230) = (2301) = (3012),

a = (421)(56) = (421)(65) = (214)(56) = (214)(65),

6 = (6240)(1735) = (2406)(3517) = (4062)(3517).

Циклы одной и той же подстановки можно переставлять, т.е. они коммутируют внутри этой подстановки:

(ijk)(l)(mn) = (l)(ijk)(mn) = (mn)(jki)(l) =(nm)(kij)(l),

i₂ = (02)(13) = (13)(02),    a = (142)(56) = (56)(142),

6 = (1735)(0624),     4 = (3715)(4260).

Разложению подстановки на систему независимых циклов отвечает разложение этой подстановки на систему коммутирующих множителей:

i₂ = =

= ,

a = =

= ,

=

.

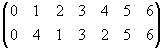
Элементарная циклическая подстановка, переставляющая два любых индекса i и j, называется транспозицией. Транспозиция обладает важным свойством: она обратна сама себе, т.е. (ij) = (ij)^–1, так как (ij)(ij)= e. Любую транспозицию (ij) можно представлять произведением смежных транспозиций по формуле:

(ij) = (j,j – 1)(j – 1, j – 2) ...        (2.25)

... (i + 2, i + 1)(i, i + 1)(i + 1, i + 2) ... (j – 2, j – 1)(j – 1, j);

например 

(48) = (87)(76)(65)(54)(56)(67)(78). 

А любой цикл может быть разложен на транспозиции, причем несколькими способами:

(ijk) = (ij)(ik) = (jk)(ji) = (ki)(kj),     (2.26)

(ijkl) = (ij)(ik)(il) = (jk)(jl)(ji) = (jk)(jli) = (ik)(lij) = (ik)(li)(lj) = ...;

например:

a = (142)(56) = (14)(12)(56) = (42)(41)(56) =

= (21)(24)(56) = (56)(14)(12),

6 = (0624)(1735) = (06)(02)(04)(17)(13)(15) =

= (26)(46)(06)(35)(37)(13) = ...

Справедливость формул (2.25) и (2.26) проверяется путем непосредственного перемножения смежных транспозиций.

Если дана подстановка, представленная в циклическом виде, то обратная ей ищется путем обратной записи последовательности всех ее индексов:

a = (ghijk)(lmn),      a^–1 = (gkjih)(lnm);

например,

6 = (0624)(1735),     6^–1 = (0426)(1537) = 4.

Транспозиции, фигурирующие в формулах (2.25) и (2.26), связанные, так как имеют какой-либо общий индекс. Все связанные транспозиции не коммутируют и не могут быть переставлены местами. Если a, b и c зависимые транспозиции, циклы или даже целые подстановки, то имеет место равенство:

abc = c^–1b^–1a^–1.

В частности, для связанных транспозиций имеем:

(ijkl)^–1 = ((ij)(ik)(il))^–1 = ((il)(ij)(ik))^–1 = (il)(ik)(ij) = (lkji).

Более общий случай проиллюстрируем примером. Пусть дано следующее произведение подстановок:

x = c^–1af ³b^–2.

Чтобы найти x^–1, нужно исходное выражение записать в обратном порядке с противоположными показателями степеней:

x^–1 = b²f ^–3a^–1c.

Правильность нахождения обратного выражения проверяется так:

x · x^–1 = (c^–1a f ³ b^–2) · (b ² f^–3 a^–1c) =

= (c^–1(a (f ³(b^–2b²) f ^–3) a^–1) c) = e.

Используя указанные свойства подстановок, записанных в циклическом виде, можно составить несколько полезных правил, которые сделают процедуру их перемножения почти механической. Вот некоторые из таких правил.

При умножении (слева или справа) смежной транспозиции на n-цикл длина последнего уменьшается на единицу и становится равной n – 1:

(abcdef...) · (cd) = (abdef...)(c),

(cd) · (abcdef...) = (abcef...)(d);

в частности,

(325614) · (56) = (32614)(5), (123) · (12) = (23)(1).

Более общее правило звучит так: произвольная транспозиция делит цикл на два несвязанных подцикла:

(abcdefgh...) · (cf) = (abfgh...)(cde),

(cf) · (abcdefgh...) = (abcgh...)(fde);

в частности,

(1234) · (13) = (12)(34),     (13) · (1234) = (14)(23).

Обратное правило, которое можно было бы назвать правилом склейки двух циклов, проиллюстрированы рис. 2.1.

Рис. 2.1

(vwxyz)(abcdefgh) · (yc) = (vwxcdefghabyz).

Склеивание циклов произойдет и в том случае, если в них имеются одинаковые индексы, которые удобно записать первыми (рис. 2.2):

(abc...) · (aij...) · (axy...) = (abc...ij...xy...).

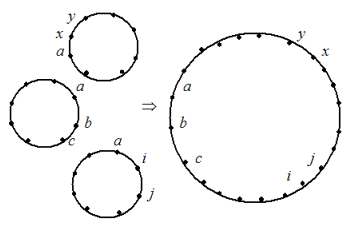
Рис. 2.2

При совпадении первых двух индексов склейки уже не получится:

(abcd...) · (abij...) = (aij...) · (bcd...).

Когда эти индексы в циклах переставлены местами, склейка снова возможна, но уже с выпадением одного из индексов:

(abcd...) · (baij...) = (a)(bcd...ij...).

В некоторых случаях полезными понятиями являются четность, декремент и число инверсий подстановки а. Декрементом (D) подстановки а называется разность между числом всех индексов (n) и количеством циклов (m), включая циклы единичной длины. Число инверсий (I) подсчитывается следующим образом: для каждого индекса нижней строки подстановки а определяется количество стоящих правее его меньших индексов, затем полученные результаты складываются. Четность подстановки a определяется четностью числа транспозиций (T), на которые можно разложить подстановку. Если декремент и число инверсий являются нечетными, то и число транспозиций также будет нечетным. Пусть задана подстановка:

a = =

 = (1)(253)(4)(67) = (1)(25)(23)(4)(67).

В соответствии с определениями имеем:

T = 3, D = n – m = 7 – 4 = 3,

I = 0 + 3 + 0 + 1 + 0 + 1 + 0 = 5.

К сказанному добавим: тождественная подстановка e четна, любая транспозиция — нечетна. Произведение четных подстановок и двух нечетных всегда даст четную подстановку, а умножение четной и нечетной — нечетную. С подстановками можно встретиться и при решении задач прикладной математики, в частности, при вычислении определителей. Вспомним, как ищется определитель третьего порядка:

det A = =

= a₁₁a₂₂a₃₃ + a₁₃a₂₁a₃₂ + a₁₂a₂₃a₃₁ – a₁₃a₂₂a₃₁ – a₁₂a₂₁a₃₃ – a₁₁a₂₃a₃₂.

Здесь индексы представляют собой шесть подстановок третьего порядка, причем перед четными подстановками стоит плюс, а перед нечетными – минус. Аналогично будут вычисляться определители 4-го, 5-го порядков, только число слагаемых будет равно 24, 120.