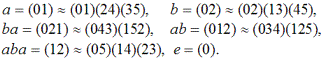Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Представления групп до 11-й порядка

Тождественный элемент e образует группу первого порядка. Обозначим ее как C₁. Несмотря на немногочисленность ее элементов, она, тем не менее, удовлетворяет всем четырем условиям определения группы; в качестве элементов g, g^–1, g₁, g₂, g₃ будет выступать один элемент e. Положительная (+1) и отрицательная (– 1) единицы образуют группу второго порядка C₂. С группой третьего порядка C₃ мы ранее еще не сталкивались. Следующие подстановки и 0,1-матрицы составят такую группу:

,

,

Базисные единицы комплексного числа {i₀, i₁, i₂, i₃} ранее нами уже рассматривались. Они образуют группу четвертого порядка C₄. Однако это не единственная группа из четырех элементов.

В самом деле, в роли образующего элемента a группы C₄, в силу условия цикличности (2.22), может выступать либо i₁, либо i₃ — в обоих случаях таблицей умножения является табл. 2.14, что также отвечает ранее приведенной таблице (табл. 2.5). Но можно в качестве образующих взять две несвязанные транспозиции a и b. В этом случае мы также получим группу четвертого порядка , но которая уже перемножается в соответствии с табл. 2.15 или, если перейти на язык только индексов, табл. 2.16.

Табл. 2.14           Табл. 2.15        Табл. 2.16

Последняя таблица нам также нужна для получения регулярных подстановок:

e = (0),   a = (01)(23),   b = (02)(13),   ab = (03)(12),

которые будут изоморфны (обозначаем как ≈) исходным подстановкам группы :

e = (0),     a = (01),     b = (23),     ab = (01)(23).

Ситуация окажется несколько иной, если в качестве образующих одной группы C₂C₃ взять несвязанные 2-цикл и 3-цикл (табл. 2.17), а в качестве образующих другой C₆ — единственный 6-цикл (табл. 2.18).

Группы шестого порядка, в отличие от групп четвертого порядка, имеют только одну коммутативную структуру, в чем можно убедиться, если соответствующие клетки табл. 2.17 и табл. 2.18 закодировать одноименными индексами – табл. 2.19. Таблицы становятся неразличимыми, т.е. группы изоморфными: C₂C₃ ≈ C₆, что на элементном уровне позволяет записать следующие соответствия:

Здесь подстановки, получающиеся при последовательном возведении в степень исходного 6-цикла a, являются не чем иным, как регулярными подстановками по столбцам табл. 2.19.

Таблица 2.17

Таблица 2.18

Таблица 2.19

Две связанные (т.е. имеющие общий нулевой индекс) транспозиции a и b также образуют группу из шести элементов, но уже некоммутативную, с принципиально иной, несимметричной относительно главной диагонали, таблицей умножения (табл. 2.20). По названию геометрической фигуры эта группа называется диэдральной и обозначается как D₃. Табл. 2.20 удобно переписать в числовых индексах — табл. 2.21, тогда можно будет составить регулярные подстановки, которые, очевидно, должны быть изоморфны исходным подстановкам группы диэдра D₃:

Таблица 2.20

Таблица 2.21

Перейдя к рассмотрению групп шестого порядка, мы пропустили группу пятого порядка. Однако нетрудно догадаться, что группы, порядок которых равен простому числу (2, 3, 5, 7, ...) всегда будут иметь и простое циклическое строение. Но чем больше делителей у порядка группы, пусть даже и одинаковых, тем разнообразнее варианты ее строения. Далее нам предстоит рассмотреть пять различных групп восьмого порядка. Анализ начнем с коммутативных групп.

Поскольку восемь можно представить тремя способами — 1 · 8, 2 · 4, 2 · 2 · 2, существуют три различных коммутативных группы: первая C₈ строится с помощью одного-единственного 8-цикла, вторая C₂C₄ — на двух несвязанных 2- и 4-циклах, наконец, третья — на трех несвязанных 2-циклах.

Из некоммутативных групп 8-ого порядка имеется две: одна обладает симметрией диэдра , другая — кватерниона . Диэдральная группа получается с помощью 4-цикла и транспозиции, индексы которой совпадают с индексами 4-цикла (табл. 2.22).

Таблица 2.22

Кватернион образуется на двух 4,4-циклах, несмежные индексы которых взаимосвязаны так, что при возведении в квадрат получается одна и та же подстановка — 2,2,2-цикл (табл. 2.23).

Таблица 2.23

Для группы диэдра были приведены только три наиболее характерных соотношения. Однако общее число возможных соотношений определяется числом перестановок всех степеней образующих a и b. Для группы кватерниона полный перечень соотношений выглядит следующим образом:

Если в качестве образующих a и b взять два несвязанных друг с другом 3-цикла, то получится коммутативная группа , которая не может быть сведена к циклической C₉. Последнее означает, что существуют две различных коммутативных группы девятого порядка:

Некоммутативных групп девятого порядка не существует. Подобная ситуация напоминает аналогичную ситуацию, сложившуюся с группами четвертого порядка. Действительно, число 9 раскладывается на два одинаковых простых множителя — 3 · 3; число 4 также раскладывается на одинаковые простые множители — 2 · 2. Отсюда можно ожидать повторения данной ситуации на таких порядках, как 25 = 5 · 5, 49 = 7 · 7 и т.д.

Число 6 раскладывается на два различных простых множителя — 2 · 3. Как мы видели, коммутативная группа, построенная на одном 6-цикле, и коммутативная группа, построенная на 2- и 3-циклах, получились изоморфными. Можно ожидать, что группа десятого порядка (10 = 2 · 5) также имеет изоморфные коммутативные группы C₂C₅ » C₁₀. В самом деле, следующее соответствие целиком подтверждает наше предположение.

Кроме коммутативной структуры, группа 9-ого порядка, как и группа 6-ого, при b = (14)(23) имеет диэдральную структуру :

Теперь мы вправе предположить, что в ряду групп 6-го и 10-го порядков окажутся также группы 14-го (2 · 7), 22-го (2 · 11) и т.д. порядков, но не 15-го (3 · 5), поскольку число 15 нечетно, а значит диэдральной группы для него не существует.