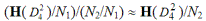Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Голоморфы диэдра и кватерниона

Введем понятие голоморфа и проанализируем его свойства. Сделаем это сначала на основе группы диэдра D₃, затем кватерниона . С этой целью составим обычную таблицу умножения для D₃ (табл. 2.34) и выпишем для нее регулярные подстановки, причем отдельно отвечающие столбцам (их называют правыми) и отдельно — строкам (левые, выделены штрихом):

Таблица 2.34

Перемножим эти подстановки:

Поскольку все левые регулярные подстановки коммутируют со всеми правыми, других подстановок здесь нет: перед нами группа 36-го порядка, которая и является голоморфом группы диэдра D₃.

Голоморф какой-либо группы G, который мы обозначим как H(G), является группой и обладает тем замечательным свойством, что среди его нормальных делителей всегда имеются две подгруппы, отвечающие его правым и левым регулярным подстановкам. Удостоверимся, что голоморф H(D₃) имеет в своем составе две инвариантные подгруппы — D₃ и D'₃. Для этого проведем морфологический анализ группы H(D₃). Прежде всего, найдем все классы сопряженности H(D₃):

В голоморфе H(D₃) имеется 15 подгрупп второго порядка, отвечающих подстановкам на транспозициях, и 4 подгруппы третьего порядка, причем две из них являются нормальными делителями —

N₁ = {0, 4, 5},         N₂ = {0, 4', 5'}.

Далее, имеется 9 подгрупп четвертого порядка типа {0, 1, 1', 11'} (все они не инвариантны). Подгруппы шестого порядка распределены следующим образом: 6 подгрупп отвечают 6-циклам и 12 диэдральных, причем 6 из них типа {0, 33', 44', 55', 12', 21'} и 6 типа {0, 11',12', 13', 4', 5'}. Сравнивая элементы этих подгрупп с элементами выписанных классов сопряженности, можно заключить, что ни одна из упомянутых 18 подгрупп шестого порядка не будет инвариантной, и только две исходные группы на регулярных подстановках D₃ и D'₃ дадут нормальные делители индекса 6, которые обозначим как

N₃ = {0, 1, 2, 3, 4, 5},         N₄ = {0, 1', 2', 3', 4', 5'}.

В нашем голоморфе содержатся шесть неинвариантных диэдральных подгрупп 12-го порядка 

{0, 1', 2', 3', 4', 5', 11',12', 13', 14', 15'},

один нормальный делитель 9-го порядка коммутативной структуры:

N₅ = {0, 4, 5, 4', 5', 44', 54', 45', 55'},

и три нормальных делителя 18-го порядка с двумя различными некоммутативными структурами:

N₆ = {0, 4, 5, 4', 5', 44, 54', 45', 55', 11', 12', 13', 21', 22', 23', 31', 32', 33'},

N₇ = {0, 1', 2', 3', 4', 5', 4, 5, 41', 42', 43', 44', 45', 51', 52', 53', 54', 55'},

N₈ = {0, 1', 2', 3', 4', 5', 4, 5, 14', 15', 24', 25', 34', 35', 44', 45', 54', 55'}.

(Можно доказать, что все подгруппы индекса 2 являются нормальными делителями своих групп.) В голоморфе неинвариантные подгруппы взаимно сопряжены, т.е. переходят друг в друга (G_i → G_j) посредством элемента g, не входящего ни в G_i, ни в G_j, например:

Найдем гомоморфизм голоморфа H(D₃) с ядром N₄, т.е. H(D₃)/N₄:

{0, 1', 2', 3', 4', 5'} → 0,   {3, 31', 32', 33', 34', 35'} → 3,

{1, 11', 12', 13', 14', 15'} → 1,  {4, 41', 42', 43', 44', 45'} → 4,

{2, 21', 22', 23', 24', 25'} → 2,  {5, 51', 52', 53', 54', 55'} → 5.

Элементы образа этого гомоморфизма удовлетворяют группе D₃:

H(D₃)/D₃ ≈ D₃,         (2.28)

— гомоморфизм голоморфа H(D₃)/D₃, ядром которого является исходная группа D₃, изоморфен (≈) внутреннему автоморфизму D₃.

Изящность формулы (2.28) объясняется тем, что центр Z группы D₃ состоит из одного тождественного элемента. Ситуация будет несколько иной в случае кватерниона, но прежде чем мы преступим к анализу , покажем на примере диэдрального голоморфа H(D₃) действие одной важной формулы, которая, однако, применима к любым группам, где имеется соответствующий расклад нормальных делителей.

Найдем три системы гомоморфных проекций —

Из 1-ой и 3-ей составим 4-ю проекцию (H(D₃)/N₁)/(N₅/N₁):

{0, 4', 5'} → 0,       {1', 2', 3'} → 1',

{1, 14', 15'} → 1,   {11', 12', 13'} → 11'.

Итак, мы получили, что

(H(D₃)/N₁)/(N₅/N₁) ≈ H(D₃)/N₅ ≈ {0, 1, 1', 11'}.

В общем случае справедлива формула сокращения наименьшего нормального делителя:

(A / C) / (B / C) ≈ A / B,     (2.29)

т.е. нормальные делители групп ведут себя подобно числовым делителям, в частности:

(36/3)/(9/3) = 36/9,     (36/6)/(18/6) = 36/18.

Теперь по изложенной методике построим голоморф на базе кватерниона H() (табл. 2.35). 

Таблица 2.35

Его порядок равен уже не 64-м, как это могло показаться на первый взгляд (8 · 8), а только 32-м. Объясняется это тем, что порядок центра кватерниона равен двум. Формула, по которой рассчитывается порядок голоморфа H(G), следующая —

| H(G) | = .

Выпишем все 32 подстановки H():

Разобьем голоморф H() на классы:

Один из кватернионов группы H(), а именно —

N₁ = {0, 1', 2', 3', 4', 5', 6', 7'},

используем для построения проекции H()/N₁:

{0, 1', 2, 3', 4', 5', 6', 7'} → 0, 

{1, 11', 3, 13', 14', 15', 16', 17'} → 1,

{4, 41', 5, 43', 44', 45', 46', 47'} → 4, 

{6, 61', 7, 63', 64', 65', 66', 67'} → 6.

Элементы {0, 1, 4, 6} факторгруппы H()/N₁ перемножаются в соответствии с таблицей умножения группы . Таким образом, для кватерниона имеем

что существенно отличается от результата для диэдра (2. 28).

В состав H() входит делитель —

N₂ = {0, 1, 2, 3, 1', 3', 4', 5', 6', 7', 11', 13', 14', 15', 16', 17'},

используем его для нахождения еще двух гомоморфизмов —

Формула сокращения наименьшего нормального делителя (2.29) для делителей кватерниона тоже подтвердилась —