Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Разложение многочлена на неприводимые множители

Рассмотрим самый общий случай. Пусть дано некоторое поле многочленов GF(q), где q = pⁿ, n — степень модуля q, а p — характеристика. Обозначим через g₁(x), g₂(x), ..., g_q–1(x) различные неприводимые многочлены над полем чисел GF(p), отвечающие примитивным корням: c₁, c₂, ... , c_{q –1}. Утверждается, что существует единственно возможное разложение многочлена x^q–1 – 1 на множители g_i(x); или, что одно и то же, каждый элемент c_i является корнем многочлена x^q–1 – 1; или, наконец, исходный приводимый многочлен можно представить в виде произведения порождающего g(x) и проверочного h(x) многочленов:

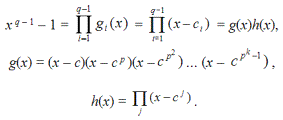
Здесь c — примитивный корень порождающего многочлена g(x), а для проверочного многочлена h(x) берутся те степени c ^j, которые не вошли в многочлен g(x). Как видим, действия с многочленами во многом схожи с действиями над числами. Приводимый многочлен вида x^q–1 – 1 играет роль составного числа a, его примитивные корни c₁, c₂, ... , c_{q –1} ассоциируются с простыми сомножителями p₁, p₂, ..., p_k, а последняя формула разложения на множители аналогична каноническому разложению составного числа a = p₁ⁿ¹ p₂ⁿ² ....p_k^nk. Многочлены g(x) и h(x) играют роль двух делителей числа a = g · h. Корни исходного многочлена играют роль базиса, по которому многочлены g(x) и h(x) могут быть разложены. Таким образом, теория полей многочленов смыкается с теорией линейных пространств. Покажем, как это осуществляется практически.

Если c — примитивный корень многочлена g(x), то

g(c) = g₀ + g₁c + g₂c² + ... + g_ncⁿ = 0.

Выразим степени корней cⁿ и cⁿ⁺¹ через линейную комбинацию младших степеней корней c, c², ..., c^n–1 (g_n = 1):

cⁿ = g₀ + g₁c + g₂c² + ... + g_n–1c^n–1, 

cⁿ⁺¹ = g₀c + g₁c² + g₂c³ + ... 

... + g_n–1(g₀ + g₁c + g₂c² + ... + g_n–1c^n–1).

Следовательно, все степени cⁱ при i > n линейно выражаются через первые n степеней; число таких комбинаций не превышает величину q – 1. Следует также иметь в виду, что не только g(c) = 0, но и 

g(c²) = g(c³) = ... = g(c^q–1) = 0.

Пример 1. Рассмотрим поле многочленов GF(q) по модулю неприводимого многочлена g(x) = x² + x + 1. Пусть примитивным корнем многочлена g(x) является корень c, тогда g(c) = c² + c + 1 = 0. Так как q = 2³ = 8, то циклический порядок корня c равен q – 1 = 7. Все корни степени i > 2 выражаются через c и c², при этом g(c) берется за модуль:

c³ = (c³ + c + 1) · 1 + (c + 1) = c + 1,

c⁴ = (c³ + c + 1) · c + (c² + c) = c² + c,

c⁵ = (c³ + c + 1) · c² + (c³ + c²) = c² + c + 1,

c⁷ = (c³ + c + 1) · c³ + (c⁴ + c³) = c² + 1.

Проверим, что числа c, c² и c⁴ действительно являются корнями многочлена g(x) = x² + x + 1:

g(c) = c³ + c + 1 = c + 1 + c + 1 = 0,

g(c²) = c⁶ + c² + 1 = c² + 1 + c² + 1 = 0,

g(c⁴) = c¹² + c⁴ + 1 = c⁵ + c⁴ + 1 = 0.

Отсюда порождающий многочлен g(x) раскладывается на следующие примитивные множители: 

g(x) = x² + x + 1 = (x + c)(x + c²)(x + c⁴),

на долю же проверочного многочлена h(x) приходятся все остальные степени корня c:

h(x) = (x + c³)(x + c⁵)(x + c⁶)(x + c⁷).

Таким образом, исходный приводимый многочлен x⁷ + 1 может быть разложен каноническим образом в расширенном поле примитивных корней (аналог поля комплексных чисел):

x⁷ + 1 = (x + c)(x + c²)(x + c³)(x + c⁴)(x + c⁵)(x + c⁶)(x + c⁷),

и неканоническим, где в скобках стоят простые сомножители (аналог поля действительных чисел):

x⁷ + 1 = (x³ + x + 1)( x³ + x² + 1)(x + 1),

а также в виде двух сомножителей:

x⁷ + 1 = g(x)h(x) = (x³ + x + 1)( x⁴ + x² + x + 1).

Если в роли модуля будет выступать порождающий многочлен g(x) = x³ + x² + 1, то его примитивный корень d даст несколько отличный цикл высших степеней корней, а именно:

d³ = d² + 1, d⁴ = d² + d + 1, d⁵ = d + 1, d⁶ = d² + d,

во всем же остальном процедура не изменится.

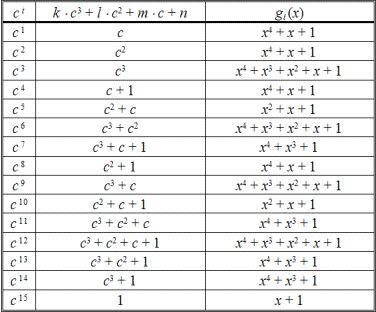
Пример 2. Составим полную таблицу неприводимых многочленов g_i(x) поля вычетов GF(2⁴) по модулю g(x) = x⁴ + x + 1 над числовым полем GF(2) (табл. 2.82).

Таблица 2.82

Заполнение таблицы неприводимых многочленов начнем с исходного многочлена. Так как

g(x) = (x – c)(x – c²)(x – c⁴)(x – c⁸),

против степеней c, c², c⁴ и c⁸ можно писать многочлен g(x). Далее, выразим все степени cⁱ через c, c² и c³, как это было сделано в предыдущем случае. Чтобы найти все остальные неприводимые множители, необходимо поступить следующим образом. Возьмем произвольный корень a = c¹⁴ = c³ + 1. Тогда

ga (x) = (x – a)(x – a²)(x – a⁴)(x – a⁸).

Так как

a² = c^28–15 = c¹³ = c³ + c² + 1,

a⁴ = c^56–45 = c¹¹ = c³ + c² + c,

a⁸ = c^112–105 = c⁷ = c³ + c + 1,

можно написать

g_a(x) = (x – c¹⁴)(x – c¹³)(x – c¹¹)(x – c⁷) =

= [x² – (c¹⁴ + c¹³)x + c¹²] · [x – c¹¹] · [x – c⁷] =

= (x² – c²x + c¹²) · (x – c¹¹) · (x – c⁷) =

= [x³ – (c¹¹ + c²)x² + (c¹² + c¹³)x – c⁸] · (x – c⁷) =

= (x³ – c⁹x² + cx – c⁸) · (x – c⁷) =

= x⁴ – (c⁹ + c⁷)x³ + (c + c)x² – (c⁸ + c⁸)x + c¹⁵.

Следовательно, против корней c⁷, c¹¹, c¹³ и c¹⁴ ставим неприводимый многочлен g_a(x) = x⁴ + x³ + 1. Затем берется следующий неизвестный корень и предыдущая процедура повторяется. Так происходит последовательное заполнение всей табл. 2.82. Проверка правильности нахождения состоит в выполнении основного тождества:

x¹⁵ + 1 = (x⁴ + x³ + 1)(x⁴ + x + 1)(x⁴ + x³ + x² + x + 1)(x² + x + 1)(x + 1).

Пример 3. Рассмотрим поле GF(3²) по модулю g(x) = x² + 1 над полем GF(3). Здесь многочлен g(x) является неприводимым, но он не является и порождающим или образующим многочленом поля, поскольку степени его корня дают единицу уже при c⁴, а не 8: 

c² = (c² + 1) · 1 + 2 = 2, 

c³ = (c² + 1) · c + 2c = 2c, 

c⁴ = (c² + 1) · c² + 1 = 1, 

c⁵ = c, c⁶ = 2, c⁷ = 2c, c⁸ = 1.

Аналогичная ситуация возникает и в числовых полях, например, в поле GF(7) элемент 3 является образующим, так как его степени порождают все элементы поля: 

3¹ = 3,     3² = 2,    3³ = 6,     3⁴ = 4,    3⁵ = 5,     3⁶ = 1, 

тогда как элемент 2 уже не будет образующим; в самом деле, его степени не дают элементы 3, 5 и 6: 

2¹ = 2,     2² = 4,    2³ = 1,     2⁴ = 2,    2⁵ = 4,     2⁶ = 1. 

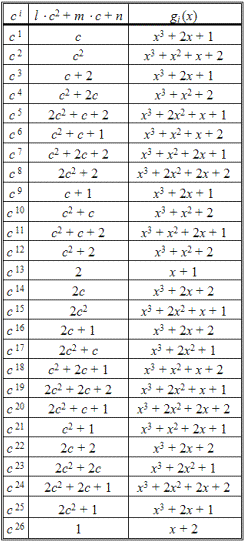
Поэтому исходным порождающим элементом нужно выбрать другой неприводимый многочлен, например, g(x) = x² + x + 2. При составлении полной таблицы неприводимых многочленов (табл. 2.83) для случая поля GF(3) действуем аналогично предыдущему примеру. Представителями классов вычетов по модулю 3 могут быть как числа 0, 1, 2, так и числа –1, 0, 1. Отсюда возникают две формы записи неприводимых многочленов с двумя проверочными соотношениями:

x⁸ + 2 = (x² + x + 2)(x² + 2x + 2)(x² + 1)(x + 1)(x + 2),

x⁸ – 1 = (x² + x³ – 1)(x⁴ – x – 1)(x² + 1)(x + 1)(x – 1).

Таблица 2.83

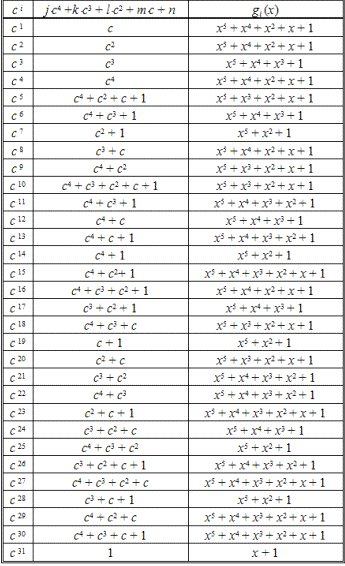
Полные таблицы неприводимых многочленов и линейные комбинации корней для полей GF(5²), GF(3³) и GF(2⁵) приведены, соответственно, в табл. 2.84, 2.85 и 2.86.

Таблица 2.84

Таблица 2.85

Таблица 2.86

Для практического задания по теме составления полной таблицы неприводимых многочленов преподаватель может менять порождающий многочлен g(x); g(x) стоит в первых строчках приведенных таблиц; в этом случае происходит перегруппировка строк.