Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.2. Морфология графа

Оптимальный путь и максимальный поток

Теперь поставим перед собой новую задачу. Пусть каждая дуга нашего упорядоченного орграфа Г₀ (рис. 3.33) снабжена весом, который складывается из суммы весов инцидентных ей вершин. За вес вершины примем ее порядковый номер. Так, у нас имеется дуга, идущая из вершины 2 в вершину 15, следовательно, вес этой дуги равен 17. Для наглядности будем считать, что она имеет длину 17 километров. Задача формулируется так: найти два пути, соответствующие минимальной и максимальной длине.

Поиск оптимального пути предполагает расстановку потенциалов для каждой вершины, т.е. образно говоря, некоего щита, на котором указывается километраж (мин./макс.). Расстановка потенциалов начинается сверху. Потенциал седьмого уровня принимается за 0; потенциалы других вершин получаются из общей длины пути, отсчитанной от вершин самого верхнего уровня до данной вершины, при этом подсчитывается длина всех путей, ведущих к этой вершине. Так, от вершины 2, принадлежащей 4 уровню, к вершинам 17 и 18, принадлежащих седьмому уровню, ведет семь путей; перечислим их по степени возрастания:

1) 17 + 32 = 49,    2) 6 + 18 + 31 = 55,     3) 6 + 18 + 32 = 56,

4) 6 + 20 + 33 = 59,     5) 6 + 20 + 34 = 60,    6) 17 + 31 + 33 = 81,

7) 17 + 31 + 34 = 82.

Следовательно, минимальный потенциал равен 49, максимальный — 82 км. Если потенциалы вершин 4 и 15, принадлежащих пятому уровню, известны, вычислений понадобится гораздо меньше; ясно, что максимальный и минимальный путь для вершины 2 определится дугой в 17 км, которая ведет к вершине 15 с потенциалами 32/65. Поэтому расстановку потенциалов и рекомендуется начать с самых верхних вершин, двигаясь последовательно по уровням вниз.

Таким образом, получаем минимальный, равный 69 км, и максимальный, равный 133 км, потенциалы. Далее остается только провести отличительными линиями дуги, инцидентные вершинам с максимальным и минимальным потенциалами, взятыми уже по каждому уровню. Если расстановку потенциалов мы начинали сверху, то проводка оптимальных путей начинается снизу. Для обратного движения сверху вниз расстановка потенциалов начинается снизу, а проводка путей — сверху. Хотя разложение вершин на классы порядка для обратного движения отличаются от прямого, длина минимального и максимального путей не меняется, т.е. если мы ехали из пункта A в пункт B по дороге с минимальной длиной пути в 69 км, то обратная поездка из пункта B в пункт A должна составить тот же самый минимальный километраж и проходить по тем же самым промежуточным пунктам.

Вообще, следует заметить, задача поиска оптимального пути в принципе может быть решена без предварительного разбиения на классы порядка. Разбиение на классы в особо запутанных графах лишь существенно облегчает этот поиск.

Рис. 3.34

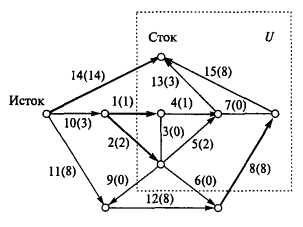
Пусть орграф Г₀ (рис. 3.34) представляет собой транспортную сеть, каждая дуга которой обладает заранее определенной пропускной способностью m (в качестве таковой примем числа, нумерующие дуги). Поставим задачу: найти максимальную пропускную способность сети между ее истоком и стоком. При нахождении общего фактического потока l необходимо помнить об очевидных правилах: сумма потоков дуг, выходящих из истока транспортной сети, должна быть равна сумме потоков дуг, входящих в сток; алгебраическая сумма потоков при любой вершине, не принадлежащей стоку или истоку, должна быть равна нулю; максимальный поток на пути от вершины i к вершине j определяется дугой k, которая имеет минимальную пропускную способность из всех дуг, принадлежащих этому пути. 

Если пропускная способность k-дуги m_k равна идущему через нее потоку l_k, то такую дугу будем называть насыщенной, а любой путь, куда она включена, — насыщенным путем. У нас k-й номер дуги (число вне скобок) определяет величину пропускной способности m_k, а число в скобках говорит о фактическом потоке l_k, т.е. в наших обозначениях имеем m_k(l_k). Общий поток транспортной сети будет максимальным l_max, если любой путь, соединяющий исток со стоком, окажется насыщенным. В этом случае поток l_max станет равным минимальной пропускной способности m_min разреза, отделяющего сток от истока.

В связи с последним замечанием дадим определение разреза применительно к транспортной сети. Пусть сток принадлежит некоторому множеству вершин U (они лежат внутри прямоугольника). Тогда разрезом S(U) называются все входящие в вершины U насыщенные дуги (в нашем случае это дуги 1, 2, 8 и 14); пропускная способность выходящих из вершин U дуг при этом не учитывается (выходящими дугами у нас являются 6 и 9). Поиск максимального потока осуществляется путем перебора всех возможных насыщенных путей от истока к стоку, причем при расстановке потока в дугах ориентируются только на три сформулированных правила. В результате перебора получим величину максимального потока:

l_max = m_min = 1 + 2 + 8 + 14 = 25.

Поскольку изображенный на рис. 3.34 орграф достаточно простой, предварительной работы по разбиению его на сильно связанные классы вершин с последующим упорядочением их между уровнями истока и стока проводить необязательно.

Разбиение на классы порядка не требуется проводить еще в двух важных случаях. Во-первых, когда иерархия вершин возникла сама собой, по причине внутренней природы математического объекта, представленного графом. Лучшей иллюстрацией здесь являются решетки, образованные подгруппами. Какой бы сложной ни была решетка, ее вершины всегда заранее разбиты на классы порядка, при этом в самом низу оказывается вершина, представляющая тождественный элемент, а на самом верху вершина, представляющая всю группу целиком. Число элементов в подгруппе является естественным критерием упорядочения. Во-вторых, упорядочение излишне в корневых деревьях: чем дальше вершина расположена от корня, который можно принять за первый класс порядка, тем выше класс порядка рассматриваемой вершины. Количество ребер, соединяющих данную вершину с корневой, здесь также является естественным критерием упорядочения. С корневыми деревьями мы, например, встречались в разделе «Логика» при рассмотрении метода резолюций (рис. 1.19). Далее мы продолжим изучение структур древовидной формы, но уже в рамках теории кодирования и автоматов.