Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.3. Кодирование, автоматы и группы на графах

Оптимальные деревья кодирования

Мы рассмотрели «азы» теории кодирования. К секретному кодированию мы больше не вернемся; корректирующее кодирование было детально рассмотрено в последнем подразделе главы «Группы»; остается рассмотреть методы оптимального кодирования, в частности, Фано и Хаффмана.

Фано предложил следующий принцип кодирования сообщений, имеющих вероятностную характеристику. Все сообщения выписываются в таблицу по степени убывания вероятности и разбиваются на две группы равной (на сколько это возможно) вероятности. Первой группе присваивается символ 0, второй — 1. Затем каждая группа вновь делится на две подгруппы равной вероятности, которым также присваиваются символы 0 и 1. В результате многократного повторения этой процедуры получается таблица кодовых слов. Продемонстрируем эту методику на конкретном примере.

Предположим необходимо закодировать 13 сообщений, причем вероятность одного из них равна 0,653, вероятность трех других сообщений равна 0,023, еще четырех — 0,027, и, наконец, пяти оставшихся — 0,034. Сумма вероятностей всех сообщений равна 1. Эти вероятности внесены во второй столбец табл. 3.13 в порядке убывания; первый столбец нумерует сообщения, а в третьем записаны окончательные коды Фано.

Таблица 3.13

n	pn	Коды
1	0.653	0
2	0.034	1000
3	0.034	1001
4	0.034	10100
5	0.034	10101
6	0.034	1011
7	0.027	11000
8	0.027	11001
9	0.027	11010
10	0.027	11011
11	0.023	11100
12	0.023	11101
13	0.023	1111

Средняя длина кодового слова равна:

l = 2, 263.

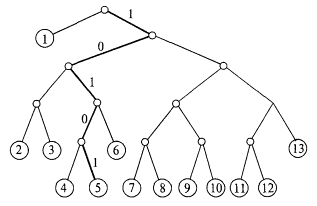
Процедура кодирования с помощью двух символов может быть представлена бинарным деревом (рис. 3.35). Длина ветвей, равная длине каждого кодового слова, определяет естественные порядковые уровни. В нашем дереве символу 0 отвечает ребро, отклоняющееся влево, а символу 1 — ребро, отклоняющееся вправо. Например, пятое сообщение имеет код 10101; соответствующая ему ветвь выделена жирной линией.

Рис. 3.35

Коды Фано по оптимальности несколько уступают кодам Хаффмана, который показал, что его методика дает предельное сжатие информационного текста. Пусть требуется закодировать все ту же последовательность сообщений. Кодовая таблица Хаффмана (табл. 3.14) начинает заполняться со столбца P₁; столбец P берем за исходный, а столбцы K, K₁, K₂ и т.д. пока оставляем без внимания. В столбце P₁ выделенная (затемненная) вероятность получается путем сложения двух наименьших вероятностей (0.023 + 0.023), остальные вероятности записываются без изменений (в нашем числовом примере все выделенные вероятности оказались на второй строке; в общем случае это не выполняется).

Таблица 3.14

n	P	K	P1	K1	P2	K2	P3	K3	P4	K4	P5	K5
1	0.653	0	0.653	0	0.653	0	0.653	0	0.653	0	0.653	0
2	0.034	1100	0.046	1011	0.050	1010	0.054	1001	0.061	1000	0.068	111
3	0.034	1101	0.034	1100	0.046	1011	0.050	1010	0.054	1001	0.061	1000
4	0.034	1110	0.034	1101	0.034	1100	0.046	1011	0.050	1010	0.054	1001
5	0.034	1111	0.034	1110	0.034	1101	0.034	1100	0.046	1011	0.050	1010
6	0.034	10000	0.034	1111	0.034	1110	0.034	1101	0.034	1100	0.046	1011
7	0.027	10001	0.034	10000	0.034	1111	0.034	1110	0.034	1101	0.034	1100
8	0.027	10010	0.027	10001	0.034	10000	0.034	1111	0.034	1110	0.034	1101
9	0.027	10011	0.027	10010	0.027	10001	0.034	10000	0.034	1111
10	0.027	10100	0.027	10011	0.027	10010	0.027	10001	0.034
11	0.023	10101	0.027	10100	0.027	10011
12	0.023	10110	0.023	10101
13	0.023	10111

Таблица 3.14 (Продолжение)

n	P6	K6	P7	K7	P8	K8	P9	K9	P10	K10	P11	K11
1	0.653	0	0.653	0	0.653	0	0.653	0	0.653	0	0.653	0
2	0.068	110	0.096	101	0.115	100	0.136	11	0.211	10	0.347	1
3	0.068	111	0.068	110	0.096	101	0.150	100	0.136	11
4	0.061	1000	0.068	111	0.068	110	0.096	101
5	0.054	1001	0.061	1000	0.068	111
6	0.050	1010	0.054	1001
7	0.046	1011

Аналогично заполняются все последующие столбцы P₂, P₃, и т.д. Далее Хаффман рассуждал следующим образом. Два сообщения с наименьшими вероятностями должны иметь одинаковые длины слов и различаться последними символами. Поэтому в последнем столбце K₁₁ против двух вероятностей выставляются символы 0 и 1. Затем идут по табл. 3.8 в обратном направлении, заполняя столбцы K₁₀, K₉ ... K₁, K. При этом символы 0 и 1 ставятся против тех вероятностей, которые в сумме давали подчеркнутую вероятность. В частности, сначала в столбце K₁₀ против вероятности 0.653 записываем 0, а против чисел 0.211 и 0.136 — 1. Затем к этим единицам приписываем новую пару символов 0 и 1, получая коды 10 и 11.

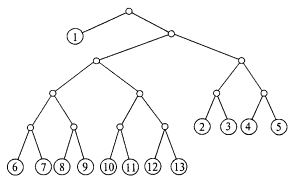
Затем обращаем внимание на подчеркнутое число 0,211 столбца P₁₀; оно получилось при суммировании чисел 0,15 и 0,096 столбца P₉, следовательно, этим вероятностям сообщаем одинаковый код 10 и приписываем по третьему символу, так что в столбце K₉ возникают коды 100 и 101. Два других кода — 0 и 11 — переписываются в K₉ из K₁₀ без изменений. Продолжая эту процедуру, мы заполняем последний кодовый столбец K, который образует окончательную систему кодовых слов. По ней вычерчиваем бинарное дерево (рис. 3.36) по тому же принципу, что и предыдущее дерево, т.е. отклонение ребра влево означает ноль, вправо — 1.

Рис. 3.36

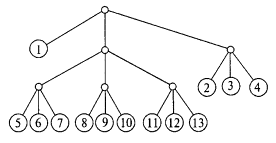
Средняя длина слова, закодированного по Хаффману, равна 2,252, что несколько меньше, чем закодированного по Фано. Большей оптимизации достичь невозможно, за исключением случая, когда вместо двух символов (0 и 1) используется три символа — 0, 1 и 2. Тринарное дерево Хаффмана изображено на рис. 3.37. По нему легко установить коды сообщений, если помнить, что для каждого ребра левое ребро означает 0, правое — 2, а серединное — 1. Методика, по которой рассчитываются коды, та же, что и в предыдущем случае, только суммируются не две наименьшие вероятности, а три. Длина кодового слова при тринарной кодировке равна 1,592, что в полтора раза выше, чем при бинарном кодировании.

Рис. 3.37

Кодовые деревья Фано и Хаффмана можно рассматривать как графическое задание алгоритмов поиска. При таком понимании средняя длина кодового слова пропорциональна стоимости поиска: чем выше частота обращения к концевой (внешней) вершине, тем меньше должна быть длина пути к ней. С этой точки зрения, рассмотренные деревья являются оптимальными только в отношении обращения к конечным вершинам. А как нужно было бы изменить алгоритм построения оптимального дерева, если бы наряду с вероятностями обращения к внешним вершинам были бы заданы вероятности обращения и к внутренним вершинам?

Пусть задан тот же ряд вероятностей, который, однако, мы разделим на две части; первая часть будет связана с вероятностью обращения к внешним вершинам a_i (табл. 3.15), вторая — с вероятностью обращения к внутренним вершинам b_i (табл. 3.16).

Таблица 3.15

Вершина	a0	a1	a2	a3	a4	a5	a6
Вероятность	0.653	0.034	0.034	0.027	0.027	0.023	0.023

Таблица 3.16

Вершина	b1	b2	b3	b4	b5	b6
Вероятность	0.034	0.034	0.034	0.027	0.027	0.023

Нахождение бинарного дерева по оптимальному достижению внешних и внутренних вершин начнем с допущения. Предположим, что дерево t_i,j является оптимальным, а внутренняя вершина b_k — его корень. Тогда это дерево можно разбить на два поддерева: t_i,k–1, являющимся оптимальным на вершинах {a_i, b_i+1, a_i+1 ... b_k–1, a_k–1}, и t_k,j — оптимальное на вершинах {a_k, b_k+1, a_k+1 ... b_j, a_j}. В отношении индексов должно выполняться условие: i ≤ k ≤ j. Суммарная частота обращения к вершинам дерева t_i,j рассчитывается по формуле:

r_i,j = q_i,j + min(r_i,k–1 + r_k,j),         q_i,j = q_i,j–1 + p(a_j) + p(b_j),

где p(a_j) и p(b_j) — вероятности обращения к вершинам a_j и b_j, а индекс k под знаком min пробегает значения от i до j. Результаты расчета оформим таблицей, в которой по горизонтали меняется значение индекса i, а по вертикали — h; при этом j = i + h. В каждую клетку таблицы будем заносить значения r_i,j и q_i,j.

Понятно, что t_i,i являются «пустыми» деревьями с корнем во внешней вершине a_i (r_i,i = 0, q_i,i = p_i). Таким образом, первая строка табл. 3.17 заполняется без предварительного расчета. Вторая строка этой таблицы также не требует больших вычислений, поскольку для деревьев типа t_i,i+1, состоящих из двух вершин и одного инцидентного им ребра, выполняется условие: r_i,i+1 = q_i,i+1, или конкретно:

q_0,1 = q_0,0 + p(a₁) + p(b₁) = 0.653 + 0.034 + 0.034 = 0.721,

q_1,2 = q_1,1 + p(a₂) + p(b₂) = 0.034 + 0.034 + 0.034 = 0.102,

q_2,3 = 0.095,    q_3,4 = 0.081,   q_4,5 = 0. 077,     q_5,6 = 0.065.

Третью строку табл. 3.17 вычисляем с учетом минимальной вероятности поддеревьев:

q_0,2 = q_0,1 + p(a₂) + p(b₂) = 0.721 + 0.034 + 0.034 = 0.789,

r_0,2 = q_0,2 + = 0.789 + 0.102 = 0.891;

q_1,3 = q_1,2 + p(a₃) + p(b₃) = 0.102 + 0.034 + 0.027 = 0.163,

r_1,3 = q_1,3 + = 0.163 + 0.095 = 0.258; и т.д.

Покажем, как выглядят конкретные формулы для вычисления вероятности r_1,6:

q_1,6 = q_1,5 + p(a₆) + p(b₆) = 0.267 + 0.023 + 0.023 = 0.313,

r_1,6 = q_1,6 + = 0.313 + (0.102 + 0.327) = 0.742.

Таблица 3.17

q0,0 = 0.653 r0,0 = 0.000	q1,1 = 0.034 r1,1 = 0.000	q2,2 = 0.034 r2,2 = 0.000	q3,3 = 0.027 r3,3 = 0.000	q4,4 = 0.027 r4,4 = 0.000	q5,5 = 0.023 r5,5 = 0.000	q6,6 = 0.023 r6,6 = 0.000
q0,1 = 0.721 r0,1 = 0.721	q1,2 = 0.102 r1,2 = 0.102	q2,3 = 0.095 r2,3 = 0.095	q3,4 = 0.081 r3,4 = 0.081	q4,5 = 0.077 r4,5 = 0.0.077	q5,6 = 0.069 r5,6 = 0.0.069
q0,2 = 0.781 r0,2 = 0.891	q1,3 = 0.163 r1,3 = 0.258	q2,4 = 0.149 r2,4 = 0.230	q3,5 = 0.131 r3,5 = 0.208	q4,6 = 0.123 r4,6 = 0.192
q0,3 = 0.850 r0,3 = 1.108	q1,4 = 0.217 r1,4 = 0.400	q2,5 = 0.199 r2,5 = 0.371	q3,6 = 0.177 r3,6 = 0.327
q0,4 = 0.904 r0,4 = 1.304	q1,5 = 0.267 r1,5 = 0.577	q2,6 = 0.245 r2,6 = 0.532
q0,5 = 0.954 r0,5 = 1.531	q1,6 = 0.313 r1,6 = 0.742
q0,6 = 1.000 r0,6 = 1.742

Здесь минимальная вероятность получается во второй строке (r_1,2 + r_3,6) при значении k = 3, следовательно, корневой вершиной дерева t_1,6 с поддеревьями t_1,2 и t_3,6 будет b₃. Итак, все внутренние вершины являются корнями своих поддеревьев; выпишем их:

b₁:   t_0,6 = t_0,0 + t_1,6,
b₂:   t_1,2 = t_1,1 + t_2,2,
b₃:   t_1,6 = t_1,2 + t_3,6,
b₄:   t_3,6 = t_3,3 + t_4,4,
b₅:   t_3,6 = t_3,4 + t_5,6,
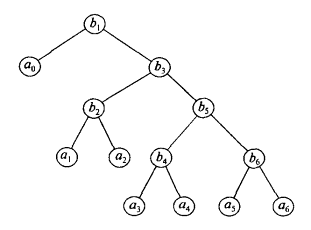
b₆:   t_5,6 = t_5,5 + t_6,6.

После этого можно приступать к вычерчиванию бинарного дерева оптимального поиска (рис. 3.38).

Рис. 3.38

Вершины построенного нами дерева можно было бы закодировать. Однако, с точки зрения теории кодирования, получающийся при этом код не был бы префиксным. Тем не менее, среднюю длину слова здесь рассчитать можно:

+ ,

где l_i — длина пути до внешней вершины a_i, l_j — длина пути до внутренней вершины b_j. Если все вычисления проделаны верно, то средняя длина кодового слова l должна в точности совпасть со стоимостью поиска по дереву t_0,6: l = r_0,6, что в нашем случае имеет место. Данное равенство играет роль проверочного соотношения.