Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

4.11. Прокол аттрактора

Из предыдущих подразделов мы усвоили, что движение от моды f 1 к моде f 2, от f 2 к f 3 и т.д. — это движение во времени. Поэтому аттрактор сохраняет амплитуду рекурсивной функции (в данном случае, функции f 1 = ax cos (x)) неизменной во времени. Однако длина волны или период колебаний — понятия условные; их восприятие различается в сознании человека, живущего в пространстве и времени. Для идеальной математики, имеющей дело с графическими изображениями и символами, эти понятия взаимозаменяемы. Человеку, конечно, лучше надолго забыть о времени и иметь дело с пространственными формами, которые можно представить. Тем не менее однонаправленность времени, как бы мы от него ни абстрагировались, настойчиво дает о себе знать в одном: мода f 2 «знает» все о моде f 1, а мода f 1 абсолютно «не догадывается» о существовании моды f 2. Именно эта черта нерушимой иерархии мод ассоциируется у нас в мозгу с их временной последовательностью подобно тому, как следствие наступает после причины, поэтому там, где есть каузальные отношения, моментально возникает ощущение времени.

Аттракторы не возводятся по прихоти человека и они не формируются под действием приливных сил Луны; они возникают сами по себе, в недрах самой рекурсивной функцией ax cos(x). Сама функция, т.е. мода f 1, о них ничего «не знает»; она свободно колеблется, равномерно увеличивая свою амплитуду. Амплитуда моды f 2 промодулирована модой f 1; на оси x появляются узлы — эмбрионы аттракторов первого рода. Слово «узел» является, пожалуй, ключевым в разгадке тайны любого аттрактора. Высшие моды как бы спотыкаются на узлах низших мод и накручиваются на них, все плотнее и плотнее их сжимая. Задача любознательного исследователя — постараться распутать аттракторный узел, завязанный тем крепче, чем выше мода. Чтобы разобраться в сплетении высших мод, нужно сперва внимательно рассмотреть узел из низших мод, а дальше картина фрактально мультиплицируется: мода f 3 сплетается с модой f 2 примерно так же, как мода f 2 сплетена с модой f 1. Тонкая структура аттрактора второго рода во многом повторяет тонкую структуру аттрактора первого рода, а микроскопическая организация аттракторов третьего рода копирует микростроение аттрактора второго рода.

Все было бы так просто, как говорится в двух последних предложениях, если бы моды были гармоническими синусоидами. К огорчению ленивых и к удовольствию пытливых, дело обстоит намного сложнее: полного тождества мод не существует, но есть лишь их подобие. Левый импульс хоть на микрон отличается от правого; последующая мода искажена чуть больше предыдущей. Эти отличия, незаметные на первый взгляд, громко заявляют о себе впоследствии. Сначала моды ведут себя наподобие фигур Лиссажу, т.е. гармонически, но потом под действием нелинейных эффектов картина радикально меняется. Гладкие, обтекаемые формы сменяются на угловатые, на уровнях аттрактора появляются подуровни субаттрактора. Потом, при едва заметном изменении коэффициента a, появляется новое видение: подуровни исчезают, появляются «лестницы» или другие прямоугольные орнаменты. Гармонический анализ не знает «трагедии», когда одна гармоника в результате суперпозиции других гармоник «проколола» бы своих сородичей. Между тем прокол аттрактора — это, пожалуй, самый драматичный, если можно так выразиться, во всяком случае, весьма зрелищный момент в жизни аттрактора.

Вначале, когда программа по наблюдению за «жизнедеятельностью» аттракторов была примитивной, тонкая структура уровней была практически недоступной для изучения, а значит, и понимания. Постепенно, по мере усовершенствования программы, стало возможно путешествовать не только в пространстве вдоль координатных осей с дискретным или непрерывным изменением масштаба, но и во времени. Картинки ожили после того, как в программу была введена подпрограмма плавного изменения коэффициента a. Запас прочности аттрактора как раз и измеряется тем, какие перепады коэффициента a он в состоянии выдержать (здесь не надо забывать о высокой чувствительности формы мод в зависимости от изменения величины коэффициента a). Может быть, кто-то из наших читателей наблюдал в микроскоп за делением клетки на две новые или следил в телескоп за динамикой солнечных пятен и протуберанцев. Так вот, слежение по монитору компьютера за всеми перестройками тонкого строения аттракторных уровней — не менее захватывающее зрелище. В любом случае от этого наблюдения вы получите гораздо больше удовольствия, чем от любой, самой убойной компьютерной игры. К сожалению, завораживающая феноменология хранит полное молчание относительно сущности данного явления. Можно часами следить за метаморфозами тонкой структуры, разбить весь динамический процесс на крохотные отрезки, но так и не уловить момент, когда «куколка оборачивается бабочкой». При увлекательном наблюдении за динамическими процессами время бежит незаметно. Сколько мимолетных часов было проведено за экраном дисплея, но многие вопросы так и остались тайной за семью печатями.

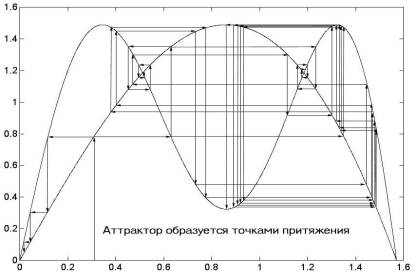
Начнем с того, что не совсем ясен механизм зарождения аттрактора, а потому остается темным и момент его разрушения. Аттрактор, как было сказано, суть линия, в нашем случае, прямая или ломаная, которая удерживает амплитуды всех мод на определенном уровне, что выглядит как их «притяжение» к данному уровню. Эта линия образована «точками притяжения», с которыми мы хорошо знакомы по предыдущим подразделам. Единственное дополнение, о котором здесь нужно обязательно упомянуть, состоит в том, что притягивающие точки образованы не только пересечением вершины моды с прямой диагональю f 0, но и пересечением одной моды с другой.

Рис. 4.56

На рис. 4.56 показано такое пересечение мод; кривые изображают моды f 1 и f 2, но из-за фрактальной природы всех мод на их месте могут оказаться моды f 101 и f 102 или f 357 и f 358. На нашем рисунке итерационный процесс начался с x = 0,3; далее можно идти либо влево, либо вправо, что все равно — любой путь, а их здесь бесчисленное множество, приведет к одной из четырех точек притяжения (две точки находятся внизу: в начале координат и в районе x = 1,6; и две точки расположены вверху, приблизительно на уровне 1,2). Главное в итерационном процессе, чтобы на его пути стрелки шли последовательно от f 1 к f 2, от f 2 к f 1, от f 1 снова к f 2 и т.д., а на какую ветвь f 1 и f 2 указала стрелка — не столь уж важно. Далее нужно отчетливо понимать, что сам итерационный процесс «не есть дело рук человеческих». Прочерченные стрелки призваны убедить лишь нас самих в том, что указанные четыре точки действительно обладают свойствами притяжения, но они останутся таковыми и без нашего вычерчивания стрелок.

Часто говорится и пишется, что аттрактор не имеет толщины, будто это божественный нимб, к которому устремляется всё бренное. К такому идеальному представлению об аттракторе нужно подходить осторожно, иначе будет непонятен механизм захвата амплитуд. Да, аттрактор состоит из точек притяжения, но точки разбросаны по некоторой области и не образуют какой-то непрерывной линии. Исключение составляет, быть может, так называемый ноль-аттрактор, когда все точки притяжения выстраиваются вдоль оси абсцисс. В общем случае аттракторный уровень имеет зримую толщину и обладает тонкой структурой, которую «издали» не разглядишь. Однако именно там, в этой хитроумно организованной области, зарождаются силы притяжения аттрактора и образуются микроуровни субаттракторов. Прокол аттрактора — это почти мгновенное исчезновение его способности удерживать амплитуды мод на строго определенном и достаточно низком уровне; они устремляются от него в противоположные стороны, иногда на астрономически большие расстояния.

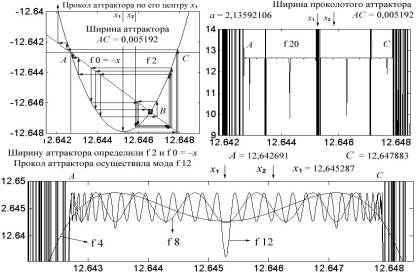
Рис. 4.57

Типичный прокол аттрактора показан на рис. 4.57. Ширина аттрактора определяется отрезком АС = 0,005192; середина его расположена в точке x₁ = 12,645287. Если итерационный процесс стартует из этой центральной точки, то стрелки выведут его сначала правее точки С, а затем выше точки А, что означает прокол аттрактора в точке x1. Но если стартовать из точки x₂, то стрелки, — каким бы путем ни идти, — непременно выведут к одной из трех точек притяжения — А, В или С. В правом верхнем окне данного рисунка показан аттрактор от моды f 20, который при коэффициенте а = 2,13592106 оказался проколотым в нескольких симметрично расположенных местах. Заметный прокол аттрактора осуществила, собственно, уже мода f 12, что видно по нижнему фрагменту рис. 4.57. Говоря о завораживающей природе прокола, мы имеем в виду волнующий вопрос: какая сила заставила выдвинуться моду f 12, ведь этому движению предшествовали многочисленные перестройки всей тонкой структуры аттрактора, не приводившие к проколу? Почему бы этой живой структуре еще раз не перестроиться так, чтобы ни одна из высших мод не вышла за пределы, очерченные низшими модами?

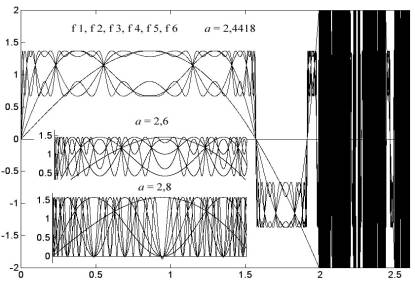
Рис. 4.58

За перестройкой тонкой структуры мод лучше всего наблюдать по Большому аттрактору, где по оси ординат один-единственный нулевой уровень имеет огромную толщину: от –1,5 до +1,5. В широком диапазоне изменения коэффициента а этот аттрактор первого рода, в силу природы функции cos (x), существует в виде двух симметричных податтракторов, которые мы будем называть аттрактором-плюс и аттрактором-минус. Рис. 4.58 зафиксировал тонкую структуру мод f 1 – f 6 при а = 2,4418 и а = 2,6, а также при а = 2,8, когда появились первые признаки прокола. Дальнейшее увеличение коэффициента даже на малую величину (0,015) приводит к росту амплитуды согласно старшинству мод (рис. 4.59). Однако ни одна из мод f 1 – f 6 при этих значениях а не вырывается за общие границы Большого аттрактора; происходят лишь проколы аттрактора-плюс и аттрактора-минус и выход старших мод за их пределы. Прокол всего Большого аттрактора наступит при гораздо большем коэффициенте, а именно, при а = 3,3429, когда произойдет полное слияние аттрактора-плюс с аттрактором-минус и образуется общая и единообразная тонкая структура Большого аттрактора (рис. 4.60) как раз отображает два таких момента.

Рис. 4.59

Рис. 4.60

Прокол протекает по одному и тому же сценарию, независимо от рода аттрактора. На рис. 4.61, где изображен аттрактор второго рода для нечетных мод, хорошо видно, как после многочисленных перестроек тонкой структуры моды выстраиваются так, что все их максимумы складываются для нанесения удара. В центре аттрактора произошло сложение пяти мод: f 3, f 5, f 7, f 9 и f 11, т.е. наибольшего числа мод; на этом участке и произошел максимальный прокол. В двух симметрично расположенных точках складываются моды: f 5, f 7, f 9, f 11; они дают второй по величине прокол. Следующий прокол произойдет без участия моды f 5 и т.д.

Рис. 4.61

Таким образом, высшая мода (в данном случае мода f 11) участвует во всех, больших и малых, проколах; следующая мода (f 9) принимает участие через один максимум, следующая мода (f 7) — через два максимума и т.д. Такая последовательность мод как раз и объясняет характерную конфигурацию разрушения аттрактора. На рис. 4.62 прокол аттрактора второго рода модой f 19 на уровне 17,41 показан с «далекого расстояния». При a = 2,73766489 прокол произошел по середине аттрактора, где амплитуда моды вырвалась на величину примерно ±500 единиц, и еще в двух боковых местах на величину примерно ±100 единиц. Изменение коэффициента на величину 0,00000021 сделало заметным прокол еще в четырех симметрично расположенных точках. С дальнейшим увеличением коэффициента а число проколов увеличивается, расширяется и длина каждого разрушенного участка.

Рис. 4.62

Рис. 4.63

Рис. 4.64

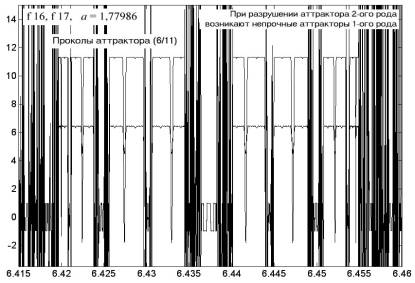
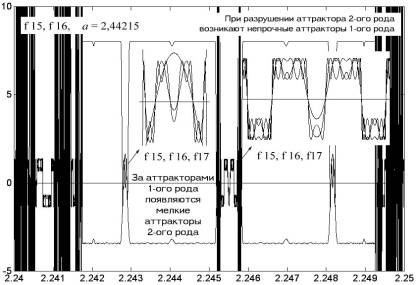
Наблюдение за разрушением аттрактора с «близкого расстояния» показывает, что в образовавшихся щелях аттрактора второго рода возникают непрочные аттракторы первого рода, о чем свидетельствуют рис. 4.63 и 4.64. «Непрочность» аттрактора в данном случае означает их небольшой запас устойчивости для высших мод. Так, при коэффициенте a = 1,77986 аттракторы первого рода существуют для мод f 16 и f 17, но они исчезнут для более старших мод. Их непрочность проявляется также в том, что эти аттракторы существуют в узких диапазонах изменения коэффициента a. Детальное изучение возникших аттракторов первого рода также показывает, что с незначительным изменением коэффициента a их тонкая структура претерпевает радикальные изменения. Эти аттракторы не прокалываются, а, скорее, перестраиваются в новые, более узкие аттракторы второго рода, образующие те же самые уровни. Сравните рис. 4.64 и 4.65; на последнем из них в центральной части при коэффициенте a = 2,44216 мы видим два аттрактора второго рода с уровнями –3 и +8, только что сформировавшиеся из мод f 15, f 16 и f 17, хотя на первом из этих рисунков при коэффициенте a = 2,44215 об их существовании ничто не напоминало. В затемненных, сильно «спрессованных» областях «спрятались» вновь образовавшиеся аттракторы второго рода. В нижнем правом окне рис. 4.64 показаны четыре аттрактора 2-го рода, образующие ±3 и ±8 уровни.

Рис. 4.65

Рис. 4.66

Аттракторы более высших родов испытывают примерно те же самые трансформации, когда коэффициент a достигает критических для них величин. На рис. 4.66 показаны девять фаз прокола аттрактора пятого рода, который в устойчивом, т.е. в непроколотом состоянии, находится в пределах a = 1,5993101 ÷ 1,5993105.

При разрушении аттрактора пятого рода, как и аттракторов второго рода, наблюдается появление непрочных промежуточных аттракторов первого рода на уровне вблизи нуля, а затем рождение новых, но уже более узких аттракторов пятого рода. Весьма любопытно наблюдать не только за перестройкой пяти уровней, но и за перестройкой аттракторов первого рода, которую, однако, совершенно не видно на представленном рисунке. Понимания динамики разрушения аттракторов можно, конечно, достичь только при кинематографическом представлении, когда коэффициент a непрерывно изменяется в заданном диапазоне. В этом случае при равномерном изменении коэффициента a хорошо видна и различная скорость протекания процессов.

Рис. 4.67

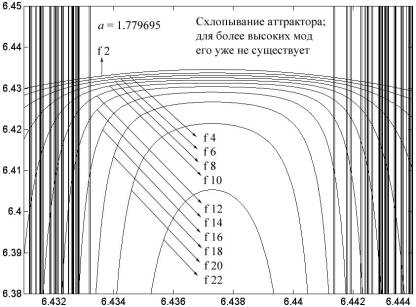
Прокол аттрактора всегда происходит при увеличении коэффициента a. А что будет наблюдаться, когда коэффициент уменьшается? В этом случае линия отсечения «макушки» от высшей моды низшей уменьшится, следовательно, ширина аттрактора тоже сузится и, при каком-то определенном коэффициенте a аттрактор совершенно исчезнет. В этом случае можно говорить о схлопывании аттрактора, причем схлопывание, как и прокол, начинается с высших мод. Сначала от аттракторного уровня отходят высшие моды, потом — низшие; моды первых порядков, обладающие наименьшей чувствительностью к изменению коэффициента a, еще долго остаются на аттракторном уровне, который давным-давно прекратил свое существование для высших мод. Схлопывание аттрактора второго рода показано на рис. 4.67. Можно, однако, говорить не о «схлопывании» аттрактора, а о его «зарождении». Тогда динамический процесс представляется следующим образом. Некая уже вполне «зрелая» мода достигает аттракторного уровня, едва касаясь его в одной или нескольких точках. Затем она все больше и больше отвоевывает для себя пространство одного или нескольких аттракторных уровней. При кинематографическом наблюдении за этим процессом с равномерным ростом коэффициента a аттрактор неравномерно раздвигает свои границы. Наконец, после многочисленных перестроек ширина его достигает критических размеров, и он прокалывается в нескольких местах по вышеуказанной схеме.