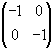Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
4.5. Аффинные преобразования
В п. 2.5 упоминались аффинные преобразования, которые образуют пространственные группы и в которых, в отличие от проективных преобразований, не действует принцип двойственности (он нам сейчас и не понадобится). Напомним, что аффинным называется такое линейное преобразование, которое помимо поворота, отражения, сжатия и растяжения (все это подгруппы аффинных преобразований) геометрических объектов, осуществляет еще сдвиг их в пространстве (иногда говорят, трансляцию). Таким образом, аффинное преобразование в состоянии выполнять все то, что не всегда доступно или удобно исполнять процедурами порождающей грамматики или прямого произведения Кронекера. Как именно с помощью аффинных преобразований достичь нужного результата, мы сейчас попытаемся разъяснить. При этом нас будет интересовать двумерный случай, поскольку фракталы чаще всего вычерчиваются в виде плоского изображения на экране монитора. В этом случае точка x = (x1, x2), испытавшая на себе аффинное преобразование, получит пространственную локализацию x' = (x'1, x'2), что в аналитической форме выражается как
x' = Ax + b,
где A — линейный оператор, b — оператор, осуществляющий сдвиг на плоскости.
Говорим «оператор», так как аффинное преобразование имеет, по крайней мере, две реализации: с помощью матриц —
и с помощью комплексных чисел. Впрочем, здесь имеется тесная взаимосвязь, так как комплексное число, как мы знаем (п. 2.1.6), можно представить матрицей. Аффинное преобразование в комплексной плоскости удобно записать в виде
x' = ax + bx* + c.
где a, b, c — комплексные постоянные аффинного преобразования, переносящие точку x в точку x' комплексной плоскости.
В качестве показательного примера возьмем ковер Серпинского, составленный из треугольников (рис. 4.10г). На рис. 4.16 показан первый шаг, когда один большой треугольник распадается на три маленьких: DABC —> DAED, DEBF, DDFC (все треугольники помещены в систему декартовых координат с указанием своих координат).
Рис. 4.16
Наша задача состоит в том, чтобы найти такие преобразования, которые бы перевели все точки большого треугольника в точки трех маленьких треугольников и расставили бы три маленьких треугольника в пространстве большого треугольника нужным образом. Вот эти три аффинных преобразования —
ΔABC → ΔAED, C → D:

ΔABC → ΔEBF, C → F:
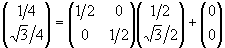
ΔABC → ΔDFC, C → C:

Эти же аффинные преобразования в комплексной форме выглядят так:



При работе с аффинными преобразованиями полезно иметь в виду следующие его свойства. Площадь большого треугольника относительно маленького уменьшилась в 4 раза. Это связано с тем, что D = det (A) = ¼. В общем случае площадь преобразованных фигур будет уменьшаться или увеличиваться в D раз. Поворот изображения на произвольный угол q, отражение его относительно оси 0x и оси 0y, а также инверсия относительно начала координат, осуществляется четырьмя матрицами:


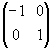
Зная, как математически корректно реализовать уменьшение масштабов геометрического образа и перенос его в другое место плоского пространства, несложно на одном из языков программирования организовать рекурсию, которая бы позволила превратить этот единичный акт в непрерывный процесс. Очевидно, программу необходимо составить так, чтобы после выполнения одного или нескольких матричных умножений система вернулась в исходное состояние, но уже относительно результирующего геометрического образа. Лучше всего эту процедуру реализовать на одном из пакетов математических программ, снабженных удобными функциями вывода графического изображения, например, на популярном пакете MATLAB.
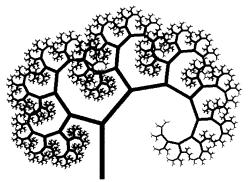
После того, как вы отладите программу по вычерчиванию ковра Серпинского можно сразу же переходить к художественному творчеству. На рис. 4.17 показан принцип построения деревьев Пифагора, в основе которых лежат «пифагоровы штаны» с одинаковыми (а) и различными (б) штанинами. На следующих двух рисунках (в) и (г) показаны фракталы после того, как машина выполнила свыше десяти итераций.
а
б
в
г
Рис. 4.17
На рис. 4.18 приведен подлинный шедевр математического искусства. Дерево выглядит настолько реалистично, что начинаешь понимать, какие удивительно простые законы лежат в основе растительного мира. В самом деле, внимательнее присмотревшись к рисунку, вы заметите, что в основе его лежит одна-единственная «косорукая» буква «Y». Ее нужно только с помощью аффинных преобразований слегка уменьшить и развернуть в пространстве так, чтобы к «рукам» исходной буквы Y приставлялись «ноги» следующих двух букв.
Рис. 4.18
Параметры аффинного преобразования ковра Серпинского занесены в табл. 4.4, где приведены параметры еще нескольких фракталов (взяты из книги Кроновера Р.М. и книги Морозова А.Д.).
а
б
в
Рис. 4.19
а
б
в
Рис. 4.20
а
б
в
Рис. 4.21
а
б
в
Рис. 4.22
Таблица 4.4
Рис.
a11
a12
a21
a22
b1
b2
4.16
0,5000
0,0000
0,0000
0,5000
0,0000
0,0000
4.16
0,5000
0,0000
0,0000
0,5000
0,5000
0,0000
4.16
0,5000
0,0000
0,0000
0,5000
0,2500
0,4330
4.19а
0,4000
–0,3733
0,0600
0,6000
0,3533
0,0000
4.19а
–0,8000
–0,1867
0,1371
0,8000
1,1000
0,1000
4.19б
0,1950
–0,4880
0,3440
0,4430
0,4431
0,2452
4.19б
0,4620
0,4140
–0,2520
0,3610
0,2511
0,5692
4.19б
–0,0580
–0,0700
0,4530
–0,1110
0,5976
0,0969
4.19б
–0,0350
0,0700
–0,4690
0,0220
0,4884
0,5069
4.19б
–0,6370
0,0000
0,0000
0,5010
0,8562
0,2513
4.19в
0,5000
0,0000
0,0000
–0,5000
0,5000
0,5000
4.19в
0,0000
–0,5000
–0,5000
0,0000
0,5000
0,5000
4.19в
–0,5000
0,0000
0,0000
–0,5000
0,5000
1,0000
4.20а
0,2550
0,0000
0,0000
0,2550
0,3726
0,6714
4.20а
0,2550
0,0000
0,0000
0,2550
0,1146
0,2232
4.20а
0,2550
0,0000
0,0000
0,2550
0,6306
0,2232
4.20а
0,3700
–0,6420
0,6420
0,3700
0,6356
–0,0061
4.20б
0,5000
0,0000
0,0000
–0,5000
0,0000
1,0000
4.20б
0,0000
0,5000
0,5000
0,0000
0,0000
0,0000
4.20б
0,5000
0,0000
0,0000
0,5000
0,5000
0,0000
4.20в
0,7000
0,0000
0,0000
0,7000
0,1496
0,2962
4.20в
0,1000
–0,4330
0,1732
0,2500
0,4478
0,0014
4.20в
0,1000
0,4330
–0,1732
0,2500
0,4445
0,1559
4.20в
0,0000
0,0000
0,0000
0,3000
0,4987
0,0070
4.21а
0,5000
0,2887
0,2887
–0,5000
0,0000
0,0000
4.21а
0,5000
–0,2887
0,2887
–0,5000
0,5000
0,2887
4.21б
0,4641
0,4641
0,4641
–0,4641
0,0000
0,0000
4.21б
0,4641
0,4641
0,4641
–0,4641
0,6222
–0,1965
4.21в
0,5000
0,5000
0,5000
–0,5000
0,0000
0,0000
4.21в
0,6000
–0,2000
–0,2000
–0,6000
0,4000
0,2000
4.22а
0,0000
–0,7000
0,7000
0,0000
0,0000
0,0000
4.22а
0,7000
0,0000
0,0000
0,7000
0,3000
0,0000
4.22б
0,6000
–0,6000
0,6000
0,6000
0,0000
0,0000
4.22б
0,5300
0,0000
0,0000
0,5300
–0,5300
0,0000
4.22в
0,0000
–0,7070
0,7070
0,0000
0,0000
0,0000
4.22в
0,5000
0,5000
–0,5000
0,5000
–0,5000
0,5000
Программ по вычерчиванию фракталов сейчас существует видимо-невидимо. Однако мы не будем рассматривать не только какие-либо конкретные программы, но даже более или менее подробные алгоритмы. Дело в том, что разнообразные машинные программы вариационной подгонки параметров по симплексной процедуре, поиска оптимального пути в графе, определения максимального потока в транспортной сети, нахождения классов сопряженности у заданной на подстановках группе и многое-многое другое резко увеличило бы объем этой и без того объемной книги. Проблема заключается еще и в том, что подобного рода материал очень быстро устаревает. Дело в конце концов не в самих картинках, а в том конструктивном подходе, который используется для их вычерчивания.