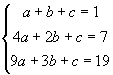Конструктивная математика
Акимов О.Е.
21. Арифметические ряды и таблицы
Рассмотрим табл. 14, в которой приведены так называемые арифметические ряды, дающие коэффициенты разложения бинома Ньютона n-ой степени:
(1 + x)n = 1 + nx + n(n – 1)x2/2! + n(n – 1)(n – 2)x3/3! + ...
... + n!xk/(n – k)!k! + ... (8)
Таблица 14
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 1 1 1 1 1 1 1 1 1 ... p1 1 2 3 4 5 6 7 8 9 ... p2 1 3 6 10 15 21 28 36 45 ... p3 1 4 10 20 35 56 84 120 165 ... p4 1 5 15 35 70 126 210 330 495 ... p5 1 6 21 56 126 252 462 792 1287 ... p6 1 7 28 84 210 462 924 1716 3003 ... p7 1 8 36 120 330 792 1716 3432 6435 ... p8 1 9 45 165 495 1287 3003 6435 12870 ... ... ... ... ... ... ... ... ... ... ... ... Биноминальные коэффициенты для n = 1, 2, 3, ... выставлены в косые ряды, начиная с верхнего левого угла табл. 14, а именно: {1, 1}, {1, 2, 1}, {1, 3, 3, 1} и т.д. Сумма биноминальных коэффициентов дает соответствующую степень 2, что вытекает из формулы (8) при подстановке x = 1:
1 + 1 = 21, 1 + 2 + 1 = 22, 1 + 3 + 3 + 1 = 23, ...
Элементы табл. 14 обладают другими замечательными свойствами: каждый последующий элемент складывается из двух предыдущих, стоящих на предыдущей строке и в предыдущем столбце, например: 56 = 35 + 21, 6435 = 3003 + 3432 и т.д. Кроме того, любой элемент получается в результате сложения всех предшествующих ему элементов либо на предыдущей строке, либо в предыдущем столбце, например:
495 = 1 + 8 + 36 + 120 + 330,
495 = 1 + 4 + 10 + 20 + 35 + 56 + 84 + 120 + 165,
3003 = 1 + 8 + 36 + 120 + 330 + 792 + 1716,
3003 = 1 + 6 + 21 + 56 + 126 + 252 + 462 + 792 + 1297.
Такая регулярность построения таблицы приводит к закономерностям в формулах для получения последовательностей чисел по горизонтальным (pi) и вертикальным (qi) рядам:
p0 = q0 = 1,
p1 = q1 = n/1!,
p2 = q2 = n(n + 1)/2!, (9)
p3 = q3 = n(n + 1)(n + 2)/3!,
p4 = q4 = n(n + 1)(n + 2)(n + 3)/4!, ...
Видно, что формулы (9) для горизонтальных и вертикальных рядов отличаются от диагональных формул для биноминальных коэффициентов (8) только знаком, стоящим внутри каждой скобки. Кто-то, возможно, посчитает индуктивный способ установления формул (9) недостаточным и попытается найти им подкрепление в каком-нибудь аналитическом выводе, например, из формул (8) или из двух вышеприведенных свойств таблицы, больше узнать об объективном устройстве числовых рядов. Поиск объективно существующих, но пока неведомых нам связей далек от формально-логического манипулирования символами; он будет походить скорее на методику исчисления.
Табл. 14 мы строили элемент за элементом, ряд за рядом по строго определенным законам. Нарушение этих закономерностей в 10 или 1010 рядах невозможно (если только мы сами этого не захотим), а значит, невозможен сбой формул для p10 или p1010. Сумма чисел натурального ряда, т.е. наша исходная формула (1) из предыдущего п. 20, отвечает строке p2 или, что то же самое, столбцу q2 табл. 14. Успех этой формулы и ее символьное представление, помимо всего прочего, обеспечиваются еще и тем местом, которое отведено числам, стоящим в соответствующей строке и столбце. Формуле (6), которую мы не смогли доказать графическими способами, естественным образом отводятся следующие строка (p3) и столбец (q3). Так возникает целый каскад единообразных формул.
Чтобы найти формулу для сумм квадратов, которые дают последовательность чисел 1, 5, 14, 30, 55, и т.д. (мы ее тоже не смогли определить), нужно построить новую таблицу арифметических рядов, где в качестве одной из строк выступал бы квадратичный ряд. Нам посчастливилось открыть закономерность для сумм кубов (формула (3)), но как быть с суммами чисел, возведенных в четвертую, пятую и другие высшие степени? Здесь нет иного пути, как только последовательное конструирование таблиц арифметических рядов. К их строительству мы сейчас приступим, но прежде сделаем небольшое замечание в отношении табл. 14.
Если элементы арифметического ряда pn обозначить через a1, a2, a3, ..., элементы ряда pn–1 через b1, b2, b3, ..., элементы ряда pn–2 через c1, c2, c3, ... и т.д., то можно составить систему разностей 1-го порядка — b1 = a1 – 0, b2 = a2 – a1, b3 = a3 – a2, ..., разностей 2-го порядка — c1 = b1 – 0, c2 = b2 – b1, c3 = b3 – b2, ... и т.д. Известно, что именно операция вычитания лежит в основе процедуры дифференцирования. Если взять производную от целочисленной квадратичной функции p2, то в результате получим линейную функцию:
.
В нашем случае при переходе от третьей ко второй строке также происходит понижение степени полинома, но уже без добавления константы 1/2, что можно записать как
d(p2) = p1 = n.
Движение по таблицы снизу вверх и справа налево отвечает природе дифференцирования. Обратное движение по таблице, связанное с суммированием ее элементов, соответствует интегрированию:
d(pn) = pn–1, d(qn) = qn–1,
= pn+1,
= qn+1.
Важно понять, что эти две операции математического анализа в первую очередь основываются на элементарных арифметических операциях вычитания и сложения, и только во вторую очередь на операции предельного перехода к бесконечно малым разностям (Δx → 0) или к бесконечно большому числу деления (n → ∞).
Таблица 15
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 — 2 2 2 2 2 2 2 2 ... p1 1 3 5 7 9 11 13 15 17 ... p2 1 4 9 16 25 36 49 64 81 ... p3 1 5 14 30 55 91 140 204 285 ... p4 1 6 20 50 105 195 336 540 825 ... p5 1 7 27 77 182 378 714 1254 2079 ... p6 1 8 35 112 294 672 1386 2640 4719 ... p7 1 9 44 156 450 1122 2508 5148 9867 ... p8 1 10 54 210 660 1782 4290 9438 19305 ... ... ... ... ... ... ... ... ... ... ... ... Теперь перейдем к рассмотрению табл. 15, которая уже не симметрична относительно своей диагонали. Ее строительство началось с третьей строки p2, где записаны квадраты чисел натурального ряда. Остальные элементы вычисляются из знакомого нам принципа: каждый последующий элемент складывается из двух предшествующих, например: 9 = 2 + 7, 9438 = 5148 + 4290 и т.д. В табл. 15 для всех элементов выполняются те же соотношения, что и для табл. 14, в частности:
660 = 1 + 9 + 44 + 156 + 450,
660 = 2 + 7 + 16 + 30 + 50 + 77 + 112 + 156 + 210,
4719 = 2 + 15 + 64 + 204 + 540 + 1254 + 2640,
4719 = 1 + 7 + 27 + 77 + 182 + 378 + 714 + 1254 + 2079.
Формулы, по которым вычисляются элементы горизонтальных и вертикальных рядов, будут такими:
p0 = 2,
p1 = (2n – 1)/1!,
p2 = n(2n + 0)/2! = n2,
p3 = n(n + 1)(2n + 1)/3!,
p4 = n(n + 1)(n + 2)(2n + 2)/4!,
p5 = n(n + 1)(n + 2)(n + 3)(2n + 3)/5!, ...
q0 = 1,
q1 = (n + 1)/1!,
q2 = n(n + 3)/2!,
q3 = n(n + 1)(n + 5)/3!,
q4 = n(n + 1)(n + 2)(n + 7)/4!,
q5 = n(n + 1)(n + 2)(n + 3)(n + 9)/5!, ...
Числа, стоящие в диагональных рядах, начиная с верхнего левого угла табл. 15, также представляют собой коэффициенты регулярных полиномов либо ri, либо si вида:
r1 = x + 2, s1 = 2 x + 1,
r2 = (x + 1)(x + 2), s2 = ( x + 1)(2x + 1),
r3 = (x + 1)2(x + 2), s3 = ( x + 1)2(2x + 1),
r4 = (x + 1)3(x + 2), ... s4 = ( x + 1)3(2x + 1), ...
Если в r- и s-полиномах раскрыть скобки, то перед различными степенями x как раз и будут стоять указанные коэффициенты. Для этих коэффициентов выполняются следующие соотношения:
1 + 2 = 3 · 20, 1 + 3 + 2 = 3 · 21, 1 + 4 + 5 + 2 = 3 · 22, ...
В связи с общим видом табл. 15 заметим, что представляют определенный интерес именно несимметричные таблицы, так как если бы первый столбец табл. 15 состоял из 2, то мы вновь имели бы дело с предыдущим случаем, отображенным табл. 14, у которой все элементы были бы умножены на 2. Аналогичная ситуация возникнет при p0 = q0 = 3 и т.д.
Таблица 16
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 — — 6 6 6 6 6 6 6 ... p1 — 6 12 18 24 30 36 42 48 ... p2 1 7 19 37 61 91 127 169 217 ... p3 1 8 27 64 125 216 343 512 729 ... p4 1 9 36 100 225 441 784 1296 2025 ... p5 1 10 46 146 371 812 1596 2892 4917 ... p6 1 11 57 203 574 1386 2983 5874 10791 ... p7 1 12 69 272 846 2232 5214 11088 21879 ... p8 1 13 82 354 1200 3432 8646 19734 41613 ... ... ... ... ... ... ... ... ... ... ... ... Наконец, рассмотрим табл. 16, в четвертой строке стоят кубы чисел натурального ряда. Строение этой таблицы аналогично строению табл. 15. Для ее элементов выполняются знакомые нам соотношения, в частности:
127 = 36 + 91, 2892 = 1296 + 1596, ...,
574 = 1 + 10 + 46 +146 + 371
и т.д. Горизонтальные и вертикальные ряды чисел удовлетворяют системе формул:
p0 = 6,
p1 = 6n – 6,
p2 = 3n2 – 3n + 1,
p3 = n3,
p4 = [n(n + 1)/2]2 = n(n + 1)(6n2 + 6n + 0)/4!,
p5 = n(n + 1)(n + 2)(6n2 + 12n + 2)/5!,
p6 = n(n + 1)(n + 2)(n + 3)(6n2 + 18n + 6)/6!,
p7 = n(n + 1)(n + 2)(n + 3)(n + 4)(6n2 + 24n + 12)/7!, ...
q0 = 1,
q1 = n + 5,
q2 = (n2 + 9n + 2)/2!,
q3 = n(n2 + 15n + 20)/3!,
q4 = n(n + 1)(n2 + 21n + 50)/4!,
q5 = n(n + 1)(n + 2)(n2 + 27n + 92)/5!,
q6 = n(n + 1)(n + 2)(n + 3)(n2 + 33n + 146)/6!,
Ряды p- и q-формул прерываются, когда закономерность их построения становится очевидной. Так, для q-формул определенную сложность вначале представляет поиск коэффициентов в последней скобке. В частности, коэффициенты перед n удовлетворяют условию: разность двух соседних коэффициентов дает число шесть:
15 – 9 = 21 – 15 = 27 – 21 = 33 – 27 = ... = 6.
Но свободные члены квадратичной формы удовлетворяют уже более сложной системе равенств:
20 – 2 = 18 = 3 · 6, 50 – 20 = 30 = 5 · 6,
92 – 50 = 42 = 7 · 6, 146 – 92 = 54 = 9 · 6, ...
И все же для отыскания коэффициентов нужна какая-то общая методика, так как даже, например, для третьей строки {1, 7, 19, 37, 61, ...} практически невозможно чисто визуальным путем уловить закономерность получения очередного члена ряда. Такая методика существует. В частности, для p2 нужно составить систему из трех уравнений и решить ее:
Полученный результат: a = 3, b = –3, c = 1.
Для нахождения коэффициентов p5 требуется уже решить систему из шести уравнений:
ее решение: a = 1/20, b = 1/4, c = 5/12, d = 1/4, e = 1/30, f = 0.Затем, после составления полинома:
n5/20 + n4/4 + 5n3/12 + n2/4 + n/30 =
= n(6n4 + 30n3 + 50n2 + 30n + 4)/5!,
его нужно попытаться упростить, поделив многочлен, стоящий в скобках, на двучлены (n + 1) и (n + 2). В более сложных случаях можно попытаться отыскать корни полиномов. Рассмотрим самый неприятный для нас случай.
Пусть дан числовой ряд:
1, 5, 13, 25, 45, 81, 145, 257, 439, ... ,
и нужно найти формулу для его n-ого члена.
Взяв первые три элемента, мы можем вычислить подходящий для этой цели полином: 2n2 – 2n + 1. Однако при n = 5 он дает число 41 вместо 45. Поэтому составим и решим систему из пяти уравнений. Так мы найдем новый полином: (n4 – 10n3 + 47n2 – 62n + 30)/6. При n = 5, 6 и 7 он нас устраивает, но при n = 8 дает число 253 вместо 257. Таким образом, никогда нет уверенности в правильности нахождения полинома для n-ого члена.
К счастью, нам нечего бояться подобной ситуации. Таблицы устроены так, что степень полиномов нарастает равномерно на единицу и все формулы для горизонтальных и вертикальных рядов оказываются взаимосвязанными. Впрочем, для большей уверенности здесь можно воспользоваться приемом, который применялся нами в самом первом доказательстве справедливости формулы (1) п. 20. Для табл. 16 это означает, что полином p1 верен, так как он удовлетворяет полиному p2:
(3n2 – 3n + 1) + 6(n + 1) – 6 = 3(n + 1)2 – 3(n + 1) + 1.
Полином p2 верен, так как он удовлетворяет полиному p3:
n3 + 3(n + 1)2 – 3(n + 1) + 1 = (n + 1)3 и т.д.
Нахождение r- и s-полиномов по табл. 16 не составит большого труда. Первоначальными значениями полиномов являются
r2 = x2 + 6x + 6, s2 = 6x2 + 6x + 1.
Далее можно воспользоваться рекуррентными соотношениями:
rn + 1 = (x + 1)rn, sn + 1 = (x + 1)sn.
Суммы коэффициентов полностью расписанных r- и s-полиномов удовлетворяют равенствам:
1 + 6 + 6 = 13 · 20, 1 + 7 + 12 + 6 = 13 · 21,
1 + 8 + 19 + 18 + 6 = 13 · 22, ...
Несложно написать начало числовой таблицы, где бы задающей строкой был полином p4 = n4. Для нее первым r-полиномом будет
r3 = x3 + 14x2 + 36x + 24.
Таблица со строкой p5 = n5 имеет такой r-полином:
r4 = x4 + 30x3 + 150x2 + 240x + 120.
Таким образом, мы имеем следующие ряды чисел:
1 1 2 1 6 6 1 14 36 24 1 30 150 240 120 1 62 540 1560 1800 720 ... ... ... ... ... ... ...Здесь обнаруживаются свои закономерности. Так, второй вертикальный ряд {2, 6, 14, 30, 62, ...} подчиняется простой формуле 2n – 2. Первый косой ряд {1, 2, 6, 24, 120, 720, ...} представляет собой последовательные значения факториала n!. А сейчас внимание: отношение элементов второго ряда {1, 6, 36, 240, 1800, ...} к соответствующим элементам первого ряда неожиданно дает хорошо знакомый нам ряд, подчиняющийся формуле (1):
1/1 = 1, 6/2 = 3, 36/6 = 6, 240/24 =10, 1800/120 = 15, ...
Так вот, мы утверждаем, что те закономерности, которые проявились во всех вышеприведенных таблицах, можно повернуть в сторону обоснования выражения для нахождения суммы арифметической прогрессии. Правда, мы не знаем, как сделать это седьмое доказательство формулы (1) конкретно; возможно, оно будет слишком громоздким. Однако обоснование, непременно, существует, коль скоро заветная последовательность выдала себя здесь. Еще раз подчеркнем, что к формуле суммы арифметической прогрессии мы пришли не в результате какого-то логического рассуждения, а на основе воображения, т.е. на основе образного мышления. Кроме того, мы руководствовались свободным конструктивным приемом, который определяется словами: что будет, если построить таблицу...
В самом деле, мы смотрим на табл. 16 и замечаем, что она имеет три прочерка в первых своих ячейках по сравнению с одним прочерком в двух предыдущих случаях. Что будет, если построить таблицу, у которой первая строка состояла бы из шестерок, но имелся бы только один прочерк в первой строке. Такой шаг не является логически обоснованным, скорее это наша прихоть, ведь перед нами распростерто множество дорог, и мы выбираем одну из большого числа возможных. В результате свободного выбора перед нами оказалась новая таблица чисел — табл. 17.
Таблица 17
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 — 6 6 6 6 6 6 6 6 ... p1 1 7 13 19 2 31 37 43 49 ... p2 1 8 21 40 65 96 133 176 225 ... p3 1 9 30 70 135 231 364 540 765 ... p4 1 10 40 110 245 476 840 1380 2145 ... p5 1 11 51 161 406 882 1722 3102 5247 ... p6 1 12 63 224 630 1512 3234 6336 11583 ... p7 1 13 76 300 930 2442 5676 12012 23595 ... p8 1 14 90 390 1320 3762 9438 21450 45045 ... ... ... ... ... ... ... ... ... ... ... ... Естественно, мы останавливаем свой взор на строке p3, где раньше стояли кубы чисел. Сравнивая два ряда чисел: {1, 8, 27, 64, 125, 216, 343, 512, 729, ...} и {1, 9, 30, 70, 135, 231, 364, 540, 765, ...}, мы неожиданно для себя открываем хорошо знакомый ряд чисел: {0, 1, 3, 6, 10, 15, 21, 28, 35, 56, 84, ...}. Конечно, можно было бы обмануть читателя и весь текст изложения построить так, чтобы он с железной необходимостью подводил к формуле (1). Но мы не станем разыгрывать из себя безупречную логическую машину и признаемся, что все вышло достаточно случайно.
По инерции мышления мы начинаем образовывать разности между всеми остальными элементами двух таблиц, в результате чего возникает еще одна таблица — табл. 18. Она отличается от табл. 13 первой строкой и первым столбцом, состоящими из нулей. Теперь понятно, почему разности между членами ряда p3 табл. 17 и 16 получились именно такими. Разумеется, такой результат не был случайным. Можно говорить, что он со всей логической необходимостью вытекает из правила сложения таблиц арифметических рядов, хотя на само правило мы наткнулись случайно.
Таблица 18
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 — — — 0 0 0 0 0 0 ... p1 — — 1 1 1 1 1 1 1 ... p2 — 1 2 3 4 5 6 7 8 ... p3 0 1 3 6 10 15 21 28 36 ... p4 0 1 4 10 20 35 56 84 120 ... p5 0 1 5 15 35 70 126 210 330 ... p6 0 1 6 21 56 126 252 462 792 ... p7 0 1 7 28 84 210 462 924 1716 ... p8 0 1 8 36 120 330 792 1716 3432 ... ... ... ... ... ... ... ... ... ... ... ... Если разность между табл. 17 и 16 дала табл. 14, то нельзя ли, например, к табл. 16 соответствующим образом прибавить табл. 15? Да, такой «эксперимент» удается осуществить, в результате получаем табл. 19.
Таблица 19
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 — — — 1 1 1 1 1 1 ... p1 — — 14 20 26 32 38 44 50 ... p2 — 8 22 42 68 100 138 182 232 ... p3 1 9 31 73 141 241 379 561 793 ... p4 1 10 41 114 255 496 875 1436 2229 ... p5 1 11 52 166 421 917 1792 3228 5457 ... p6 1 12 64 230 651 1568 3360 6588 12045 ... p7 1 13 77 307 958 2526 5886 12474 24519 ... p8 1 14 91 398 1356 3882 9768 22242 46761 ... ... ... ... ... ... ... ... ... ... ... ... Вновь устремляем свои взоры на ряд p3 и вновь сравниваем его с рядом p3 табл. 17. Разность этих рядов опять порождает ряд {0, 0, 1, 3, 6, 10, 15, 21, 28, ...}. Следовательно, табл. 19 отличается от табл. 17 на табл. 14, у которой нулями уже заняты первые два столбца (табл. 20).
Таблица 20
q0 q1 q2 q3 q4 q5 q6 q7 q8 ... p0 — — — — 0 0 0 0 0 ... p1 — — — 1 1 1 1 1 1 ... p2 — — 1 2 3 4 5 6 7 ... p3 — 0 1 3 6 10 15 21 28 ... p4 0 0 1 4 10 20 35 56 84 ... p5 0 0 1 5 15 35 70 126 210 ... p6 0 0 1 6 21 56 126 252 462 ... p7 0 0 1 7 28 84 210 462 924 ... p8 0 0 1 8 36 120 330 792 1716 ... ... ... ... ... ... ... ... ... ... ... ... Так шаг за шагом приходит глубокое понимание природы таблиц арифметических рядов. Оказывается, каждая такая бесконечная таблица представляет собой цельный математический объект. Эти объекты, как и числа, можно складывать и вычитать. Они поддаются классификации, в частности, по количеству штрихов в левом верхнем углу таблицы, т.е. по числу ячеек, для которых не выполняются провозглашенные ранее принципы образования элементов. К нулевому классу можно было бы отнести табл. 14. Это единственная таблица, которая имеет одинаковые формулы для вертикальных и горизонтальных рядов. Она играет роль единичного элемента в множестве арифметических таблиц. Затем идут таблицы первого класса типа табл. 4.10 и 4.12. Они отличаются тем, что полиномы, выражающие общие члены горизонтальных и вертикальных последовательностей имеют действительные корни.
Формулы p- и q-полиномов для табл. 15 уже выписывались. Приведем соответствующие формулы для табл. 17:
p0 = 6,
p1 = (6n – 5)/1!,
p2 = n(6n – 4)/2!,
p3 = n(n + 1)(6n – 3)/3!,
p4 = n(n + 1)(n + 2)(6n – 2)/4!,
p5 = n(n + 1)(n + 2)(n + 3)(6n – 1)/5!,
p6 = n(n + 1)(n + 2)(n + 3)(n + 4)(6n – 0)/6!,
p7 = n(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)(6n + 1)/7!,
p8 = n(n + 1)(n + 2)(n + 3)(n + 4)(n + 5)(n + 6)(6n + 2)/8!, ...
q0 = 1,
q1 = (n + 5)/1!,
q2 = n(n + 11)/2!,
q3 = n(n + 1)(n + 17)/3!,
q4 = n(n + 1)(n + 2)(n + 23)/4!,
q5 = n(n + 1)(n + 2)(n + 3)(n + 29)/5!, ...
Сопоставляя эти формулы с формулами для табл. 15, мы улавливаем закономерности их написания. Теперь без всяких таблиц мы сможем выписать p- и q-формулы с p0 = 3, 4, 5 и т.д. Ко второму классу таблиц можно отнести табл. 16, которая имеет три ячейки с прочерком и для которой p- и q-полиномы не полностью раскладываются на простые двучлены с действительными корнями. В их состав входят квадратичные сомножители с комплексными корнями. К третьему классу относятся таблицы типа табл. 19, у которой уже шесть прочерков. В состав p-полиномов у нее входит неразложимые кубы:
p3 = (6n3 + 6n2 – 12n + 6)/3!,
p4 = n(6n3 + 20n2 – 6n + 1)/4!,
p5 = n(n + 1)(6n3 + 34n2 + 16n + 4)/5!, ...
Табл. 18 и табл. 20 дают представление о роли «единичного элемента» в множестве арифметических таблиц и поясняют правила сложения и вычитания со сдвигом на строку или столбец. Мы также припоминаем, что складывать и вычитать можно не только целые положительные числа; следовательно, таблицы могут быть заполнены действительными или комплексными числами. Если читатель захочет, он может остаток своей жизни целиком посвятить изучению свойств этих таблиц: они вполне достойны этого. Что же касается нас, то позвольте закончить этот подраздел повторением главного вывода.
Всякий скажет, что таблицы и p-, q-формулы ничего общего не имеют с рисунками. Тем не менее, установленные закономерности пришли к нам благодаря внимательному рассматриванию их. Цифры и буквенные обозначения мы обозреваем точно так же, как точки и линии, образующие рисунки, т.е. при рассмотрении и тех и других задействованы одни и те же психические механизмы. Через цифры и буквы к нам приходят понятия о числе, формуле и отношениях между ними; через точки и линии — понятия о фигурах. По формулам и таблицам мы свободно скользим взглядом так же, как по геометрическим рисункам, и здесь нет места для логики. От формулы к формуле мы нередко приходим через процедуру вычисления. Логика, конечно, помогает общаться и делает понятным все то, что затем излагается другим людям, но на этапе исследования или даже первого знакомства с неведомым объектом она плохая помощница. Молодым людям, жаждущим познать истину вещей, нужно усвоить именно философию конструктивизма.