О.Е. Акимов

Устройство Солнечной Системы

Часть 3

Samuel Earnshaw (1805 – 1888)

Самуэль Ирншоу — английский священник и математик, прославившийся своим вкладом в теоретическую физику. С 1831 по 1847 работал в Кембридже. По причине неважного здоровья перешел на службу в церковь Святого Михаила, которая находилась там же, в Кембридже. После он вернулся в свой родной город Шеффилд, где учительствовал и служил в качестве капеллана. Как священнослужитель, опубликовал несколько богословских трактатов и проповедей. Как ученый, написал ряд научных статей и книг по математике (решение дифференциальных уравнений в частных производных) и по физике (в основном, в области оптики и акустики). Его имя сделалось широко известным после математического доказательства в 1839 году физической теоремы, которая сейчас носит его имя. Она касалась, собственно, задачи, которую независимо от Ирншоу в 1878 году исследовал Альфред Майер, но уже эмпирическим путем (см. УСС Часть 2). Теорема Ирншоу доказывает принципиальную неустойчивость левитации, т.е. свободно плавающих постоянных магнитов. Впрочем, его теорема касается взаимодействия любой природы, в частности, кулоновского и гравитационного.

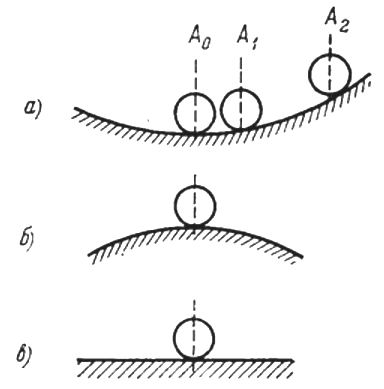
Суть проблемы нам хорошо известна. Для устойчивого равновесия системы объектов требуется создать ситуацию, когда всякое отклонение покоящегося объекта тут же порождало воздействие, которое возвращало бы систему в прежнее состояние. Но согласно теореме Гаусса, например, для кулоновской системы зарядов, поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри нее электрическому заряду. Причем — и это сейчас главное — он не зависит от расположения зарядов внутри замкнутой поверхности; поток безразличен к распределению зарядов. Вот если бы расположение зарядов влияло на величину потока напряжённости, т.е. при каком-то распределении зарядов существовало бы минимальное значение потока, то при всяком, самом микроскопическом отклонении хотя бы одного из зарядов система тут же "свалилась" бы в точку минимума. Из нее уже невозможно было бы систему вывести в какое-то другое состояние; она неизменно "скатывалась" бы в яму. Эту ситуацию — устойчивое, неустойчивое и безразличное состояние системы обычно иллюстрируют следующими картинками.

Варианты устойчивости системы


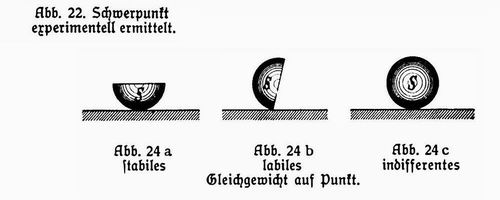
В своей "Немецкой физике" Филипп Ленард продемонстрировал
три указанных случая несколько иной картинкой.

В предыдущей части уже говорилось, что Альфред Майер опубликовал свои исследования в журналах Amercian Journal of Science, 3rd ser., 15 (1878), 276–277, 477–478; 16 (1878), 247–256; Scientific American, supp. 5 (1878), 2045–2047. К сожалению, сегодня тексты этих статей являются собственностью указанных журналов и не могут быть выставлены для свободного чтения всем желающим. Дж. Дж. Томсон довольно детально рассказал нам об опыте Майера, правда, из его повествования невозможно понять знал или не знал он о теореме Ирншоу, которая тесно связана с экспериментом с плавающими магнитами

Альфред Майер и Дж. Дж. Томсон

Американские журналы позапрошлого века нам недоступны. Зато доступен текст прошлого века хорошо известной "Истории физики" П.С. Кудрявцева ("Просвещение", 1971 год). Ниже приводится две страницы из 3-го тома, где рассказывается об атоме Дж. Дж. Томсона, вспоминается работа Вильяма Томсона (лорда Кельвина) и опыты А.М. Майера.

Две страницы из "Истории физики" П.С. Кудрявцева

При чтении страниц, нужно помнить, что 7-уровневые конфигурации оказались разбитыми на две части — три ряда оказались на 144 страницы, а следующие четыре ряда — на 145. Первая конфигурация включает 94 магнита (24 + 21 + 17 + 15 + 11 + 5 + 1 = 94). За ним идут столбцы с 95 магнитами, 96, 97, 98, 99 и, наконец, со ста штуками.

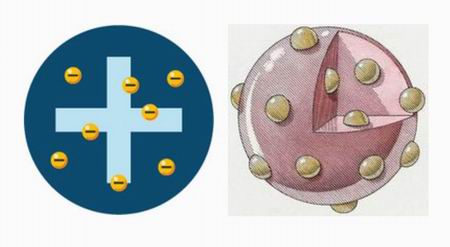
Обратите внимание, Кудрявцев отмечает: "Модель Томсона отнюдь не статическая, как часто ее представляют в учебниках. Это динамическая модель оболочек". Я впервые такое читаю. Мы ведь привыкли слышать, будто Томсон предложил модель атома в виде пудинга с изюмом.

Модель пудинга с изюмом


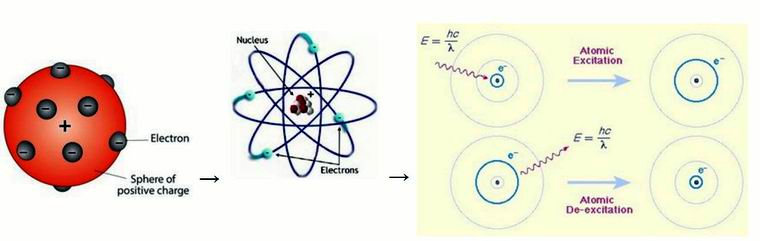
А так изображают развитие атомных моделей от Томсона через Резерфорда к Бору.
Реальная история атомной физики выглядела намного сложнее.

В первой работе Томсона 1897 года, рассказывающей об эксперименте Майера, приводилась таблица расположения магнитов, в которой мы видим неопределенность в расположении, например, 28 и 30 магнитов, представленных парой конфигураций. Это демонстрация теоремы Ирншоу в действии.

Одинаковые конфигурации магнитов с числом 28 и 30 штук
свидетельствуют о неопределенности, которая продиктована
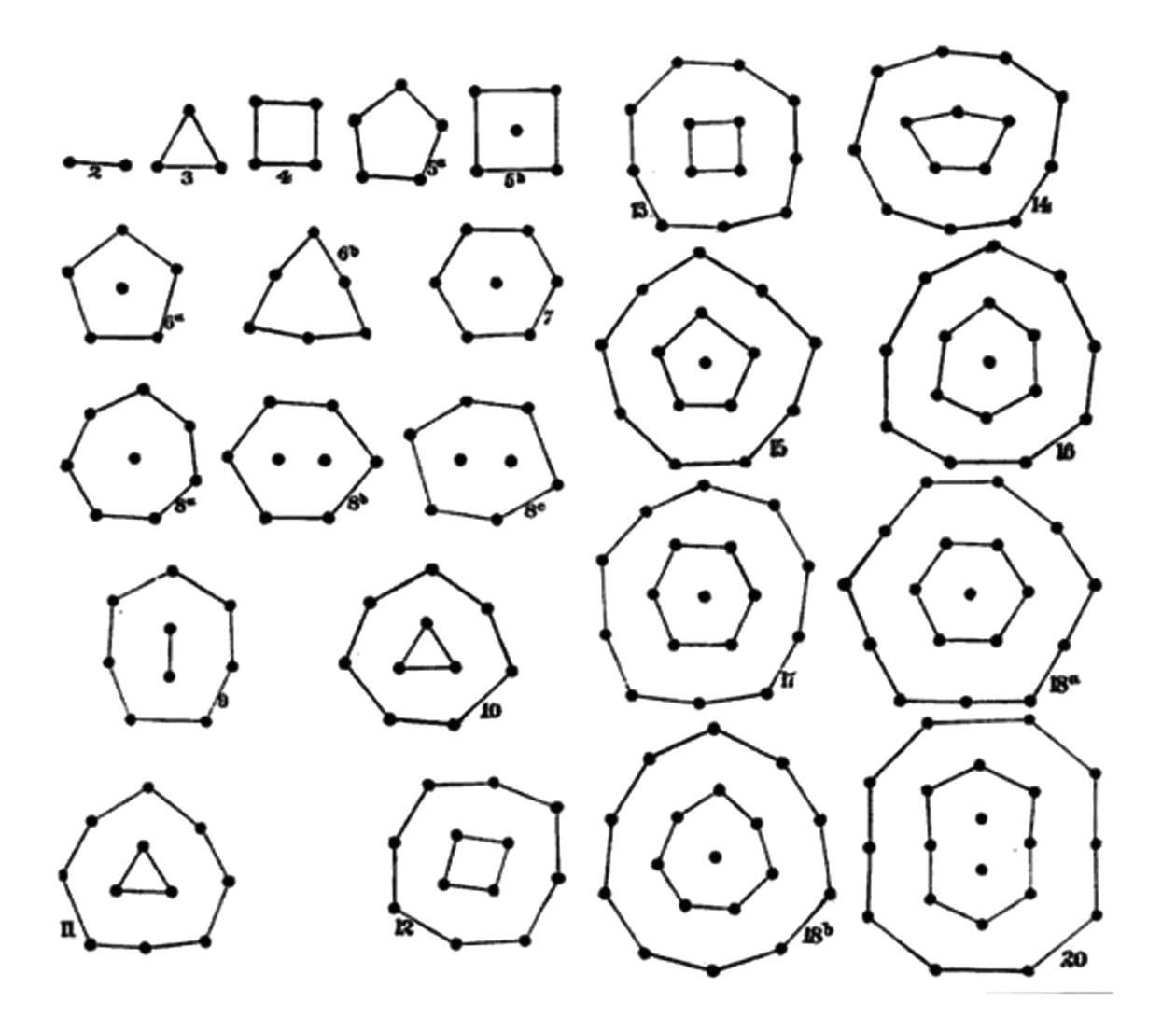
теоремой Ирншоу.

Сейчас, дорогой читатель, я попрошу вас напрячь пространственное воображение. Знаю по опыту моей борьбы с релятивистами, это дается с большим трудом. Но всё-таки попробуем посмотреть на хорошо знакомые конфигурации другими глазами.

Графические конфигурации, полученные Майером.
Схемы с 5, 6, 8 и 18 магнитами тоже демонстрируют наоднозначность


Две пары схем с 5 и 6 магнитами вычерченные отдельно.
К этим схемам применима терминология теории графов.

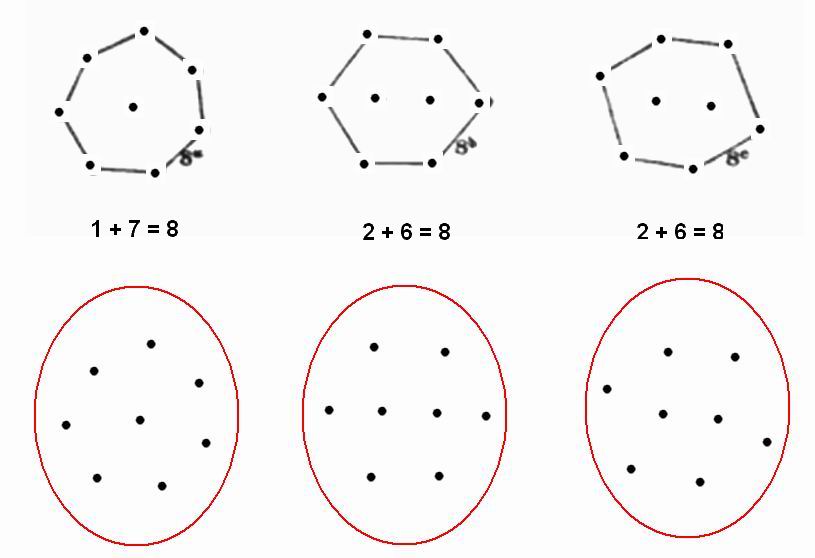
Попробуйте мысленно удалить из этих графов с 5 и 6 вершинами соединительные линии (согласно математической науке, они называются ребрами графа). Сделаем это явным образом для трех графов с 8 вершинами; получим следующий рисунок:

Три графа с 8 вершинами и три множества одних только вершин.

В результате получились некие хаотически разбросанные группы вершин, без видимого упорядочения. Чувствуется, что Майер был просто загипнотизирован идеей кольцевого строения атомов. Он искусственно внес порядок там, где его изначально не было.

Переход от первой конфигурации вершин 8^a ко второй 8^b достигается малыми перемещениями, что позволяет делать нам теорема Ирншоу. Аналогичными перемещениями можно осуществить переход от второй конфигурации 8^b к третьей 8^c. Таким образом, Майер мог бы нарисовать не три, а, скажем, 4, 5 или 6 различных графических вариантов.

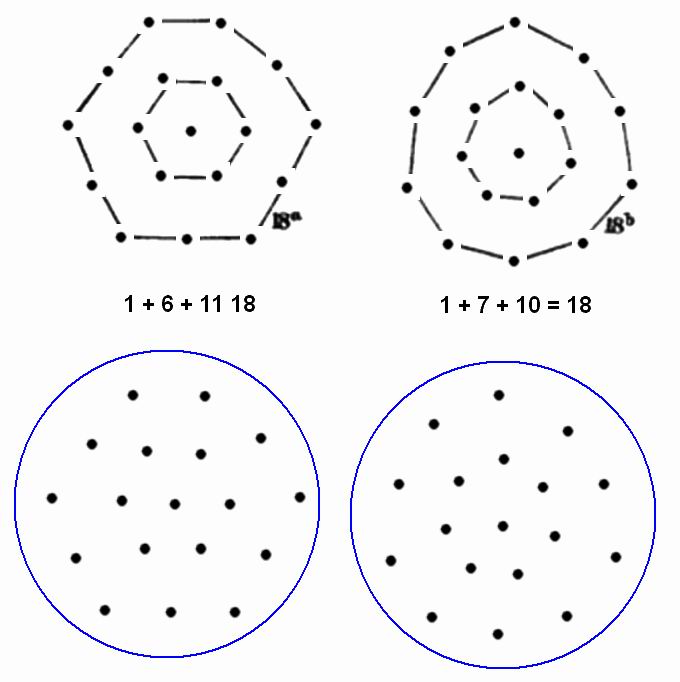
У нас имеется две модификации графов с 18 вершинами. Вычертим их отдельно, а, затем, уберем у них все ребра. В итоге, получим два случайных набора точек. Ясно, что путем их мысленного перемещения можно представить сколько угодно подобных наборов.

Два графа с 18 вершинами.

Почему Майер изобразил только два набора с 18 вершинами — не известно. По той же теореме Ирншоу конфигураций может быть сколь угодно много. Никаких особых граничных условий теорема не накладывает. Она позволяет передвигать магниты произвольным образом, по крайней мере, на малые расстояния. При этом никаких возвращающих сил не возникает. Поэтому, путем большого числа крошечных перемещений можно радикально изменить первоначальную картину расположение магнитов.

Таким образом, сегодня я смотрю на картинки, размещенные в предыдущей части УСС, а также на свои рассуждения в разделе Эфир (Часть 2) Модель атома Томсона и пылевая плазма и в других местах, совершенно иначе. Думаю, Майер невольно занимался графической подгонкой, а Томсон числовой — он ведь сам не проводил экспериментов, полагаясь на числовые результаты своего предшественника. Так что его исследования вполне сродни занятиям по нумерологии. Единственным критерием отбора конфигураций для Майера было, по-видимому, желание изобразить картину вложенных друг в друга колец более или менее "красиво".

На страницах 144 и 145 "Истории физики" П.С. Кудрявцева, как мы помним, выписаны 7-этажные конфигурации с числом магнитов от 94 до 100 штук. Представляете, сколько произвола в этих схемах! Несчастный автор поверил Томсону, Томсон — Майеру. Слава богу, на нас, надеюсь, эта цепочка "веселых" заблуждений прервется. Дальше обсуждать эту "игру" не хочется. Еще вчера я раздумывал, как закончить третью часть УСС. Сегодня решил ничего не писать — хватит тратить на эту ерунду свои интеллектуальные усилия.