Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.1. Операции логики Буля

Пересечение, двойственность, дополнение

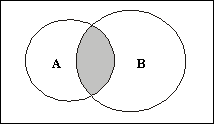
Пересечением множеств A и B называется множество A ∩ B, содержащее те элементы из A и B, которые входят одновременно в оба множества. Для нашего числового примера будем иметь:

A ∩ B = {1, 2, 4, 6} ∩ {2, 3, 4, 8, 9} = {2, 4} = C₃.

Диаграмма Эйлера – Венна для пересечения изображена на рис. 1.4.

Рис. 1.4

То, что x принадлежит одновременно двум множествам A и B можно представить выражением:

x ∈ A ∩ B = (x ∈ A) ∧ (x ∈ B),

где ∧ — символ логической связки и, которая называется конъюнкцией.

Таблица 1.2

x1	x2	y = x1 ∧ x2
0	0	0
1	0	0
0	1	0
1	1	1

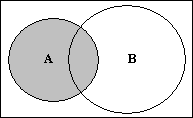
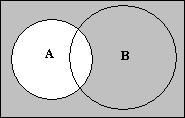
Если в таблице истинности для конъюнкции (табл. 1.2) все нули заменить единицами, а все единицы — нулями, то в итоге получим табл. 1.1. Этот факт определяет взаимную двойственность конъюнкции и дизъюнкции. Для любой логической операции можно найти двойственную. Представим себе операцию, в результате которой окажутся заштрихованными области C₁ и C₃, образующие множество A (рис. 1.5). Затем еще одну операцию, которая охватит две другие области — C₀ и C₂, не входящие в A, что обозначается как A (рис.1.6).

Рис. 1.5

Рис. 1.6

Если объединить заштрихованные области на обеих диаграммах, то получим все заштрихованное множество 1; пересечение же A и A даст пустое множество 0, в котором не содержится ни одного элемента:

A ∪ A = 1, A ∩ A = 0.

Аналогичные равенства выполняются и для логических функций, которые имеют соответствующие названия:

y = x ∨ x = 1 — тавтология,

y = x ∧ x = 0 — противоречие.

Тавтология — это всегда истинное логическое выражение, какое бы при этом значение ни принимала переменная x. Противоречие, напротив, всегда ложное выражение.

Множество A дополняет множество A до фундаментального множества V (или 1); отсюда название: дополнительное множество A, или дополнение как операция. Дополнение к логической переменной x, т.е. x (не-x), называется чаще всего отрицанием x.

После введения операций пересечения и дополнения все четыре области C_i на диаграмме Эйлера – Венна можно выразить следующим образом:

C₀ = A ∩ B,     C₁ = A ∩ B,     C₂ = A ∩ B,     C₃ = A ∩ B.

Путем объединения соответствующих областей C_i можно представить любую множественную операцию, в том числе и само объединение:

A ∪ B = (A ∩ B) ∪ (A ∩ B) ∪ (A ∩ B).

Все это распространяется и на логику:

y = x₁ ∨ x₂ = (x₁ ∧ x₂) ∨ (x₁ ∧ x₂) ∨ (x₁ ∧ x₂).