Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.4. Введение в логику высказываний

Метод резолюций

Рассмотрим еще один полуконструктивный метод доказательства истинности логических клауз, в котором используется так называемый принцип резолюций. Этот принцип играет роль аксиомы порядка и вместе с тем порождает очень эффективную конструктивную процедуру. Суть его сводится к тому, что два посылочных дизъюнкта с противоположными термами всегда можно склеить в один дизъюнкт, в котором уже не будет противоположных термов:

X ∨ A, Y ∨ A ⇒  X ∨ Y,

где X и Y — произвольные термы или целые дизъюнкты с любым набором термов, включая ноль; A и A — произвольные термы.

При последовательном применении принципа резолюций происходит уменьшение числа букв, вплоть до их полного исчезновения. Исходную клаузу возьмем в форме конъюнктивного противоречия:

Р₁, Р₁, ... , Р_n ⇒  0.

Докажем справедливость правила отделения:

А, А → В ⇒  В   или   0 ∨ А, А ∨ В, В ∨ 0 ⇒  0.

Здесь три дизъюнкта. Склеивая их последовательно, получаем в результате ноль, который говорит о несовместимости заключения и посылок. Это свидетельствует о справедливости исходной клаузы. 

Принцип резолюций целиком заменяет аксиому порядка, поскольку сама эта аксиома может быть доказана в рамках метода резолюций. Действительно,

А, В ⇒  А,    А, В, А ⇒  0 ,    0, В ⇒  0.

Обращаем внимание на то, что посылка В здесь вообще не используется. Это необходимо иметь в виду: необязательно использовать все посылки (их число часто бывает избыточным) — главное получить ноль. Пусть дана клауза:

А → В, С ∨ А, В → С ⇒ А.

Доказательство ее справедливости следует начать с приведения ее в нормальную конъюнктивную форму:

А ∨ В, С ∨ А, В ∨ С, А ⇒ 0.

Выпишем по порядку все посылки и далее начнем их склеивать (справа от дизъюнкта записаны номера используемых дизъюнктов):

1. А ∨ В, 
2. С ∨ А,
3. В ∨ С,
4. А,
5. А ∨ С,    (1,3)
6. В,           (1,4)
7. А ∨ В,    (2,3)
8. С,           (2,4)
9. А,           (2,5)
10. С,         (3,6)
11. В,         (3,8)
12. С,         (4,5)
13. В,         (4,7)
14. 0.          (4,9)

Подобная стратегия поиска нуля очень непродуктивна. Если к этой же задаче подойти более творчески, то ноль обнаружится на четвертом шаге от начала поиска:

5. В  (1,4),     6. С  (2,4),     7. В  (3,6),     8. 0 (5,7).

До сих пор мы говорили о форме конъюнктивного противоречия. Исходя из принципа двойственности, метод резолюций можно сформулировать относительно дизъюнктивной тавтологии, при этом принцип резолюций, естественно, изменится:

X ∧ Y ⇒ X ∧ A; Y ∧ A.

Докажем одну и ту же клаузу двумя способами — в форме противоречия и форме тавтологии. Пусть дана клауза:

А, А → В, В → (А → С) ⇒  С.

Доказательство в форме противоречия выглядит так:

А, А ∨ В, В ∨ А ∨ С, С ⇒  0.

Если по порядку пронумеровать четыре посылки, то ноль получается при следующих склейках:

5. В (1,2),     6. А ∨ С (1,6),     7. С (3,5),     8. 0 (4,7).

Доказательство в форме тавтологии выглядит аналогично:

1 ⇒  А; А ∧ В; В ∧ А ∧ С; С.

Склейки:

5. В (1,2),     6. А ∧ С (1,6),     7. С (3,5),     8. 1 (4,7).

Метод резолюций легко поддается алгоритмизации. Это позволяет использовать его в логических языках программирования и, в частности, в ПРОЛОГЕ. Алгоритм склеек образует структуру древовидной формы (рис. 1.19) для следующей клаузы:

S ∨ R ∨ P, S ∨ Q ∨ R, P ∨ S ∨ R, R ∨ S ∨ P, R ∨ Q ∨ S, S ∨ Q ∨ R, P ∨ S ∨ Q, P ∨ Q ∨ R, S ∨ P ∨ R, P ∨ S ∨ R, R ∨ S ∨ Q ⇒  0.

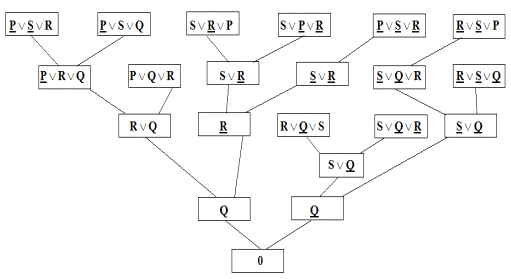
Рис 1.19