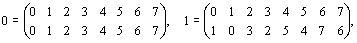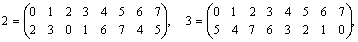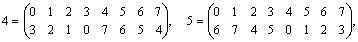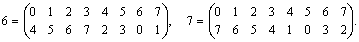Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.1. Группа и связанные с ней понятия

Подстановки

Комплексное число есть двухкоординатный вектор, кватернион – четырехкоординатный и т.д. В предыдущем разделе рассматривались базисные 0,1-матрицы, которые не дают смешиваться различным координатам числовых агрегатов и одновременно задают закон перемножения для их базисных единиц. Однако группы 0,1-матриц образуют все же операционные множества. Соответствующим субстанционным множеством для них служат 0,1-векторы-столбцы, о которых ничего не было сказано. Между тем, для 0,1-матриц комплексного числа (2.17) в качестве базиса могут выступать, например, первые столбцы этих матриц. Не оперируя 0,1-векторами, прибегнем к более эффективной методике, введя в обращение новый математический объект — подстановки.

Всякая 0,1-матрица переставляет числа в векторе-столбце, который нумерует строки этой матрицы. Например, для базисных единиц комплексного числа i₁ и i₂, имеем:

i₁ = ,

i₂ = .

Следовательно, любой 0,1-матрице можно поставить в соответствие двухрядную таблицу; в нашем случае это

i₁ = ,    i₂ = .

Такие двухрядные таблицы и называются подстановками (алгебраический термин) или перестановками (комбинаторный термин, который здесь не используется).

Пусть дана таблица перемножения индексов — табл. 2.13.

Таблица 2.13

0	1	2	3	4	5	6	7
1	0	3	2	5	4	7	6
2	3	0	1	6	7	4	5
3	2	1	0	7	6	5	4
4	5	6	7	2	3	0	1
5	4	7	6	3	2	1	0
6	7	4	5	0	1	2	3
7	6	5	4	1	0	1	2

Тогда искомая группа G регулярных подстановок, отвечающая столбцам табл. 2.13, выглядит следующим образом:

Подстановки имеют ряд достоинств перед 0,1-матрицами: во-первых, они менее громоздки, во-вторых, их проще перемножать, в-третьих, существует специальная запись подстановок, при которой сразу можно определить их степень периодичности. Имеется теорема, утверждающая, что не существует такой группы, которую нельзя было бы представить подстановками.

Покажем, как производится перемножение подстановок на примере умножения базисных единиц комплексного числа i₁ и i₂. С этой цель проследим переход индексов от одной подстановки к другой. Индекс 0 подстановки i₁ переходит в 1, а 1 подстановки i₂ переходит в 3; следовательно, в результирующей подстановке i₃ 0 будет переходить сразу в 3. Затем смотрим, во что переходит 1: 1 → 2 → 0, значит, для i₃ индекс 1 перейдет в 0. Далее, 2 → 3 → 1 и 3 → 0 → 2, отсюда 2 →1 и 3 → 2. В итоге получим подстановку i₃ вида:

i₁ · i₂ = · = = i₃.

Перемножая всеми возможными способами регулярные подстановки группы G, убеждаемся, что они дают табл. 2.13.

Легко перемножаются одновременно три или даже большее число подстановок, например:

· · = ,

здесь 0 → 2 → 3 → 1, т.е. 0 в результирующей подстановке сразу переходит в 1.

Подстановка, не переставляющая ни одного индекса, называется тождественной (нейтральной или единичной). Она отвечает единичной матрице:

e = .

Тождественными подстановками являются i₀ в базисе комплексного числа i и 0 в группе G (табл. 2.13). Две подстановки, дающие при перемножении тождественную подстановку e, называются взаимно обратными, в частности, таковыми являются подстановки i₁ и i₃ комплексного числа:

i₁ · i₃ = · = = i₀.

Подстановки 1, 2, 3 группы G являются взаимно обратными, а для подстановок 4, 5, 6, 7 обратными служат 6, 7, 4, 5, соответственно.

Чтобы из заданной подстановки а получить взаимно обратную a^–1, необходимо верхнюю строку подстановки поменять с нижней и упорядочить индексы верхней строки. Пусть

а = ,

тогда, согласно определению, будем иметь:

a^–1 = = .

Внимательный анализ всех подстановок группы G подтверждает эту взаимосвязь между исходными и обратными подстановками.