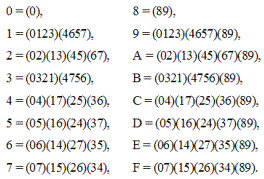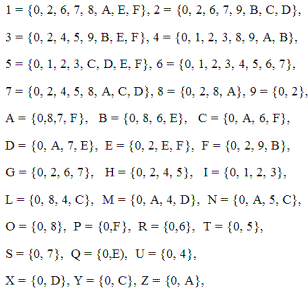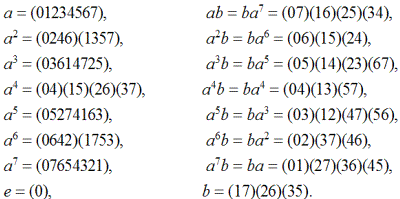Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.3. Групповые решетки из подгрупп

Решетки групп 16-го порядка

Структуры от групп 13-го, 14-го и 15-го порядков нам знакомы, поэтому не будем здесь на них останавливаться и сразу перейдем к морфологическому анализу групп 16-го порядка.

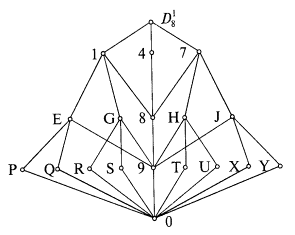
Самой простой из них является цепь из четырех звеньев структуры S(C₁₆), а наиболее разветвленной — решетка S(). Ее условно-схематическое изображение показано на рис. 2.21.

Рис. 2.21

Между полюсами имеется три уровня. Уровень 2-го и 8-го порядков состоят из 15 узлов:

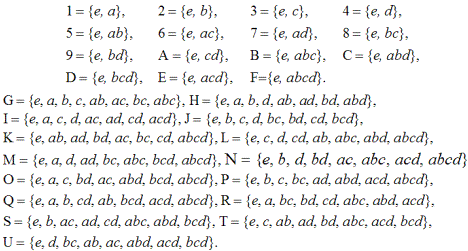
Уровень 4-го порядка образован 35 узлами. Подгруппы мы перечислим, но присваивать им специальных обозначений не будем:

Сравнивая выписанные подгруппы между собой, мы можем заключить: каждая подгруппа 2-го порядка входит в 7 различных подгрупп 4-го порядка; каждая подгруппа 4-го порядка состоит из элементов 3 подгрупп 2-го порядка (например, подгруппа {e, a, b, ab} состоит из элементов подгрупп 1, 2 и 5); каждая подгруппа 4-го порядка целиком входит в три подгруппы 8-го порядка (например, подгруппа {e, a, b, ab} входит в подгруппы G, H и Q); каждая подгруппа 8-го порядка состоит из элементов 7 подгрупп 4-го порядка. Таким образом, число подходящих связей к каждому узлу 8-го порядка и число отходящих связей от каждого узла 2-го порядка равно 7. Это, в свою очередь, означает, что число связей для узлов названных уровней у других структур, построенных на основе групп 16-го порядка, также не может превосходить число 7. Далее, число подходящих и отходящих связей для уровня 4-го порядка у других структур не может превосходить число 3.

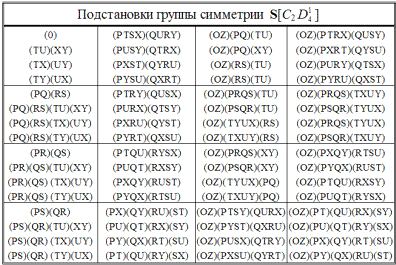
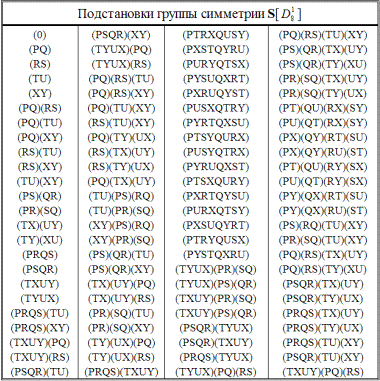
Группа S[] простая. Все ее подстановки четны. Группа содержит 32 256 элементов, которые разбиты на 12 классов. В табл. 2.61 приведены примеры подстановок, взятые из каждого класса; здесь же указано количество подстановок в классе.

Таблица 2.61

В классе C₁ выполняются известные нам антикоммутационные соотношения. Все подстановки этого класса приведены в табл. 2.62. Таблица разбита на 15 частей (по числу узлов на одном нижнем уровне); в каждую часть входит по 7 коммутирующих между собой подстановок (по числу связей, приходящихся на один узел). Последнее обстоятельство делает решетку S() непрозрачной.

Таблица 2.62

Следующей группой 16-го порядка, решетка которой вписывается в верхнеполюсную решетку S(), является группа . Прежде чем приступить к морфологическому анализу группы , нам необходимо выписать все ее подстановки:

Путаницы не произойдет, если для обозначения подгрупп (узлов) группы мы используем те же самые символы, что и для индексов подстановок:

Решетка S() изображена на рис. 2.22. Она состоит как бы из трех решеток S() — одна вверху и две внизу. Характеристика ее такова: число узлов на всех уровнях нечетно — 7, 15 и 11; число связей тоже нечетно — 1, 3, 5 и 7.

Рис. 2.22

Решетка прозрачна, так как подстановки a и b порождают группу диэдра , а коммутирующая с a и b подстановка c расширяет группу до :

a = (25)(36)(EG)(FI)(ACBD)(KM)(LN)(OZ)(PRQS)(TU),

b = (AD)(BC)(OZ)(PQ)(KM)(LN)(TU),     c = (KL)(MN)(TU)(XY).

Однако такие длинные подстановки, инвариантно переставляющие узлы на всех уровнях, можно не писать. Как и в предыдущем случае, группа симметрии S[] вполне представима 64-мя подстановками, составленными по 11 узлам только одного нижнего уровня (табл. 2.63).

Таблица 2.63

Решетка S(C₄) от коммутативной группы инверсная и состоит из двух симметрично расположенных решеток S(). Она получается из решетки S() путем удаления восьми узлов — A, B, C, D, P, Q, R, S. Инверсной подстановкой для S(C₄) является:

i = (1Z)(2X)(3T)(4O)(5Y)(6U)(79)(KF)(LI)(MG)(NE).

Решетка S(C₄) прозрачна, так как имеются три коммутирующих подстановки, образующие группу C₄:

a = (25)(36)(EG)(FI),   b = (14)(36)(EI)(FG),   c = (KLNM)(TU)(XOYZ).

Группу S[C₄] определяют подстановки, составленные по 11 узлам среднего уровня. При их нахождении очень удобно ориентироваться на хорошо известную нам группу S[], для которой ищется подгруппа, оставляющая один узел на месте (у нас это узел 7 для верхнего этажа и узел 9 для нижнего). Далее, необходимо помнить, что верхняя и нижняя подрешетки S() рассматриваемой решетки S(C₄) существуют практически независимо. Выпишем порождающие элементы двух подгрупп преобразований, действующих на этих подрешетках:

a = (EG)(FI),   a' = (KM)(LN),   b = (EFG)(8HJ),   b' = (LNM),

c = (EFGI)(HJ),     c' = (KMLN),     d = (EF)(8J),     d' = (KL).

Обратим несколько большее внимание на группу диэдра 16-го порядка . Это позволит нам понять структуру еще двух групп примерно этого же строения. С этой целью выпишем для нее все основные соотношения и подстановки :

Заметим, что помимо a и a⁷, представляющих собой 8-циклы и фигурирующих в главном соотношении, имеется еще два элемента — a³ и a⁵ — точно с таким же периодом. Если возможна группа с равенством ab = ba⁷, то нельзя ли попытаться построить еще две группы на равенствах ab = ba³ и ab = ba⁵. Такая попытка увенчается успехом, если в качестве образующих b взять, соответственно:

: b = (02)(15)(46),        : b = (04)(26).

Тогда получим следующую картину определяющих соотношений:

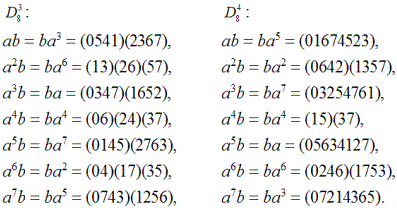
Здесь нужно не забыть о существовании еще одной группы кватернионного типа с образующими:

a = (01234567)(89ABCDEF),     b = (084C)(1F5B)(2E6A)(3D79).

Теперь выпишем все подгруппы группы диэдра. Так как решетка S() вписывается в решетку S(), нам удобно узлы подрешетки S() обозначить через узлы надрешетки S():

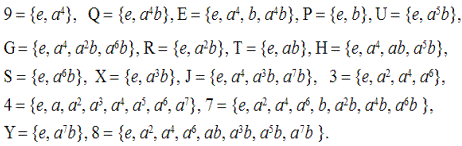
Решетка S() изображена на рис. 2.23.

Рис. 2.23

Если из этой решетки удалить четыре узла — T, U, X, Y, — получим решетку S(). Затем, если удалить еще четыре узла — P, Q, R, S, — получим решетку S(). Наконец, если из решетки S() удалить восемь других узлов: H, J, R, S, T, U, X, Y, получим решетку S().

Группа симметрии диэдральной решетки S[] состоит из 96 подстановок, которые выписаны в табл. 2.64.

Таблица 2.64

Для группы S[] все определяется уровнем 2-го порядка. Из табл. 2.64 видно, что решетка диэдра прозрачна, что нельзя сказать о других решетках этой серии, в частности:

Самым поразительным математическим фактом здесь является то, что решетка S() от некоммутативной группы является инверсионной и в точности совпадает с решеткой S(C₂C₈) от коммутативной группы. Их общей инверсионной подстановкой является

i = (19)(8E)(4Q)(7P).

Решетку S() (рис. 2.23) полезно сравнить с решеткой S() (рис. 2.16), поскольку они очевидным образом находятся в отношении порядка. Четыре узла — E, G, H, J — среднего уровня дают группу S[] » , которая является гомоморфным представлением группы S[] из восьми узлов нижнего уровня — P, Q, R, S, T, U, X,Y. Причем из рис. 2.23 можно стразу записать систему проецирования элементов группы S[] на группу S[]. Так, например, перестановка двух узлов (PQ) оставляет узел E на месте; перестановка же четырех узлов типа (PR)(QS), (PS)(QR) или (PSQR) проецируется на транспозицию (EG) и т.д.

Если построить следующую решетку S(), то ее узлы будут связаны с узлами S() аналогичным образом и группа S[] уже станет гомоморфным представлением группы S[]. Так возникает иерархия решеток от диэдральных групп, которая выражается в метарешетке MD в виде бесконечной цепи. Главное отличие диэдральной метарешетки MD от ранее рассмотренных метарешеток M_n состоит в том, что для MD цепь решетчатых вложений сопровождается цепью групповых вложений:

Рассмотрим следующие две группы 16-го порядка, которые мы обозначили как и (напомним, что и относятся к группам 8-го порядка). Для наглядности приведем основные групповые соотношения и подстановки :

Для группы дадим еще один изоморфизм на базе кватерниона:

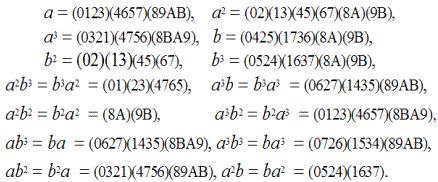
Выпишем подгруппы группы :

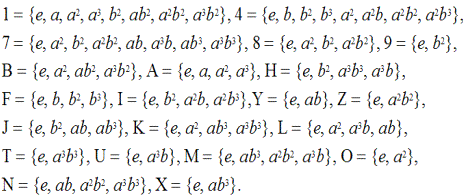
Как и в предыдущих случаях, воспользуемся обозначениями узлов решетки S(), поскольку узлы рассматриваемой решетки S() являются подмножеством узлов решетки S().

Решетка S() изображена на рис. 2.24. Между уровнями 2-го и 4-го порядка расположена подрешетка S(), что облегчает поиск группы S[]. В группе S[] 48-го порядка имеется подгруппа, изоморфная с образующими —

a = (14)(9O)(HL)(KJ)(TY)(AIBF), 

b = (14)(9O)(MN)(HKJL)(TXYU)(AFBI).

Рис. 2.24

Таким образом, решетка S() прозрачна. Узлы решетки S() и узлы инверсной ( i = (1O)(49)(7Z) ) решетки S() образуют два подмножества от множества узлов решетки S():

Отсюда можно видеть, что решетки S() и S() непрозрачны.

Перейдем к группе . Ее целиком определяют следующие простые соотношения: 

a² = b² = c² = e, abc = bca = cab. 

Из этих равенств несложно вывести вспомогательные соотношения:

acb = cba = bac, aba = cbc, aca = bcb, bab = cac,

которые позволяют составить таблицу умножения из 16 элементов группы :

{e, a, b, c, ab, ac, ba, ca, bc, cb, abc, acb, aba, aca, bab, abab}.

Удобно образующие приводить в виде регулярных подстановок, тогда при их умножении сразу получаются столбцы таблицы умножения, а не ее отдельные элементы:

a = (01)(23)(45)(67)(89)(AB)(CD)(EF),

b = (02)(16)(3E)(4C)(5B)(7F)(8D)(9A),

c = (04)(18)(2A)(3D)(5E)(6B)(7C)(9F).

Рис. 2.25

Решетка S() изображена на рис. 2.25. Если из этой решетки удалить узлы R, S, T и U, то получим решетку S(). Несмотря на внешнее различие решеток, их группы симметрии одинаковые и изоморфны полной группе куба:

S[] » S[] » O_d.