Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.1. Группы цепей графа

Элементарная группа цепей и ее решетка

Множество точек (вершин, узлов) и множество линий (ребер, дуг), которые соединяют эти точки, будем называть графом Г. Граф Г₃ (рис. 3.1а) и ему подобные конструкции из линий и точек называется полным, поскольку все его вершины связаны между собой линиями. Граф, изображенный на рис. 3.1б, полным уже не назовешь, однако линии такого частичного графа образуют полную цепь. Цепь называется полной, если она связывает все точки графа линиями без образования петель и контуров. Цепи, связывающие только часть точек (рис. 3.1в), мы рассматривать не будем и, следовательно, термин «полная» применительно к цепи можно будет опускать без риска быть непонятыми.

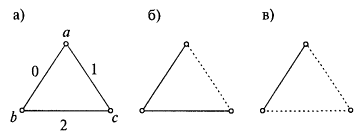
Рис. 3.1

Цепь имеет голову и хвост. Голова цепи привязывается к какой-либо точке, которую мы будем в этом случае называть привязкой. Для графа Г₃, если в качестве привязки выступает точка a, имеем две цепи abc = 02, acb = 12; если привязкой является точка b, получим еще две цепи — bac = 01, bca = 21; наконец, если c — привязка, то cab = 10, cba = 20 — цепи. Вместо шести мы на самом деле имеем только три цепи A, B и C, поскольку не столь уж важно, каким образом начинается запись цепи — с головы или с хвоста; отсюда получаем: 

A = 01 = 10,     B = 02 = 20,     C = 12 = 21.

Одной из тем этого подраздела является поиск групп преобразования цепей. Дело в том, что, скажем, цепь 01 переходит в цепь 02 путем замены линии 1 на линию 2, при этом линия 0 остается на месте. Этот переход можно записать как 12 или 21. Обратный переход цепей друг в друга осуществляется при противоположной замене линий, т.е. 12 = 21. Последовательная замена линий: сначала 12, затем 12, оставляет исходную цепь 01 тождественной самой себе. Но осуществление двух различных замен, например, 12 и 01 по отношению к исходной цепи 01, приводит к преобразованию: из 01 в 02 и из 02 в 12, что равносильно действию замены 02.

Цепи образуют субстанционное множество, а преобразования — операционное. При замене отдельных звеньев цепи удобно воспользоваться аддитивной записью. В частности, действие преобразования mn на цепь lm выразится через суммы:

01 + 12 = 02,     01 + 02 = 12,    02 + 01 = 12, ... ,

а переходы от одной цепи к другой запишутся через разности, например, преобразование A в B как A – B = 01 – 02 = 12, обратное преобразование как B – A = 02 – 01 = 12. Все остальные преобразования в Г₃ запишутся с помощью следующих простых выражений:

A – C = 01 – 12 = 02,     B – C = 02 – 12 = 01,

C – A = 12 – 01 = 02,     C – B = 12 – 02 = 01,

A – B – A = A – A = 12 + 12 = e,     B – A – B = B – B = 12 + 12 = e,

A – C – A = A – A = 02 + 02 = e,     C – A – C = C – C = 02 + 02 = e,

B – C – B = B – B = 01 + 01 = e,     C – B – C = C – C = 01 + 01 = e,

C – A – B = C – B = 02 + 12 = 01,     B – A – C = B – C = 12 + 02 = 01,

A – C – B = A – B = 02 + 01 = 12,     B – C – A = B – A = 01 + 02 = 12,

A – B – C = A – C = 12 + 01 = 02,     C – B – A = C – A = 01 + 12 = 02.

Перед нами множество элементов, удовлетворяющих условиям группы: каждое преобразование имеет обратное; последовательное действие прямого и обратного преобразований дает тождественное; для любых трех преобразований справедливо условие ассоциативности; наконец, все множество преобразований замкнуто.

Однако в группах цепей имеются и важные отличия по сравнению с ранее рассмотренными группами, а именно: не всякое преобразование g_j может последовать за преобразованием g_i. В частности, преобразование 12 не может последовать за преобразованием 02, поскольку первое отвечает переходу цепи A в цепь B, а второе — переходу цепи A в цепь C; между тем разрешен переход от A к B и от B к C. Таким образом, в графах на операционное множество накладывается жесткое ограничение, продиктованное субстанционным множеством. Своенравная природа графа проявляется и в совершенно новом делении элементов группы на классы эквивалентности. Здесь уже нет классов сопряженных элементов и классов смежности, иначе находятся подгруппы, отсутствуют делители и т.д. Покажем на примере группы G₃ от графа Г₃, как производится групповой анализ графа.

Пусть вершина a треугольника, изображенного на рис. 3.1а, является привязкой. Следовательно, она находится в особом положении относительно двух других вершин треугольника — b и c. Так возникают два класса вершин — {a} и {b, c}. Стороны треугольника также разбиваются на два класса в зависимости от степени удаленности от привязки — {0, 1} и {2}. Это деление на классы пока никак не проявляется на строении группы G₃. Привязка a определяет две цепи — B и C, для которых возможны переходы 01 и 01, принадлежащие одному классу. Вместе с тождественным преобразованием они дают элементарную подгруппу G_3a = {e, 01, 01}. Каждая привязка определяет свою подгруппу: G_3b = {e, 02, 02}, G_3c = {e, 12, 12}. Все вместе элементы G_3a, G_3b и G_3c образуют графовую группу преобразований цепей в треугольнике:

G₃ = { e, 01, 01, 12, 12, 02, 02}.

В процессе формирования группы G₃ была установлена и соответствующая иерархия элементарных подмножеств, которую, как мы знаем, удобно представлять в виде решетки S(G₃). Если наши подгруппы обозначить через числа 1, 2, 3, тождественный элемент через 0, то отношение порядка между подгруппами S(G₃) будет выглядеть так, как это показано на рис. 3.2.

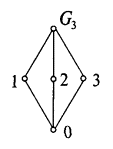
Рис. 3.2

Прежде чем переходить к анализу следующей группы, обратим внимание на то, что наименьшей группой преобразования цепей является G₂ = {e}, которая оставляет свою единственную цепь, соединяющую две вершины, в покое. Группа G₃ является первой нетривиальной графовой группой преобразования цепей с двумя образующими, неоднозначно определенными, например, такими: a = 01, b = 12. Тогда все остальные элементы группы G₃ выразятся следующим образом:

G₃ = {e, a, a, b, b, ab, ab}, где

e = a + a = b + b, ab = a + b = 01 + 12 = 02, ab = a + b = 01 + 12 = 02.

Не забудем сказать и о том, что все группы цепей коммутативны и нечетны. Проявлением аддитивной сущности графовых групп является отсутствие степеней образующих. Для мультипликативных подстановок было справедливо условие:

если   a · b = c,  то   a = c · b^–1   и   b = a^–1 · c ;

для аддитивных реберных подстановок истинным является аналогичный закон с учетом коммутативности:

если   a + b = c,   то   a = b + c и   b = a + c.