Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.1. Группы цепей графа

Группа цепей куба

Рис. 3.6

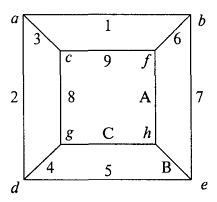
Перейдем к рассмотрению группы преобразования цепей куба Г₈ (рис. 3.6). Если в качестве привязки принять вершину a, то в зависимости от ее удаленности получим четыре класса вершин: класс 0 — {a}, класс 1 — {b, c, d}, класс 2 — {e, f, g} и класс 3 — {h}; и три класса ребер: класс 1 — {1, 2, 3}, класс 2 — {3, 4, 5, 6, 7, 8}, класс 3 — {A, B, C}. Привязка a определяет 18 цепей. Частота появления ребер в цепях распределяется по трем классам следующим образом: для класса 1 она равна 6, для класса 2 — 13 и для класса 3 — 10. Приведем список цепей, которые привязываются к вершине a:

Список разбит на два цикла: первый — с 1 по 9, второй — с 10 по 18. Внутри каждого цикла переход от одной цепи к другой осуществляется заменой одного ребра. Новое ребро появляется путем присоединения восьмой (хвостовой) вершины каждой цепи к первой (головной), третьей или пятой. Таким образом, происходит инверсия хвостовой части каждой из цепей, т.е. два, четыре или шесть хвостовых ребер присоединяются к вновь установленному ребру в обратном порядке. Так, переход от цепи 1 к цепи 2 осуществляется путем удаления ребра gd= 4 и введением ребра gh = C, при этом чередование вершин хвостовой части цепи (deh) меняется на противоположное (hed). Переход от цепи 2 к цепи 3 осуществляется путем инверсии семи хвостовых вершин (bfcghed) и т.д.; цепь 9 переходит в цепь 1 путем инверсии пяти вершин (hedgc). Аналогичная картина наблюдается во втором цикле.

Чтобы получить цепи от семи других вершин куба (рис. 3.6), достаточно в имеющихся 18 цепях произвести замену ребер в соответствии с семью подстановками, которые вместе с тождественной образуют коммутативную группу типа С₂С₄:

b = (1752)(36B4)(89AC),     c = (19)(28)(5C)(7A), 

d = (1257)(34B6)(8CA9),     e = (15)(27)(3B)(46)(8A)(9C), 

g = (185A)(2C79)(34B6),     f = (1A58)(297C)(36B4),

h = (1C)(2A)(3B)(46)(59)(78).

В результате действия группы подстановок получим 18 × 8 = 144 цепи. Однако в кубе можно провести только 72 цепи. Удвоение числа можно понять из анализа хвостовых вершин приведенных цепей. На восемнадцать головных вершин класса 0, т.е. вершин a, приходится по четыре хвостовых вершины класса 1, т.е. вершин b, c, d, и шесть вершин h класса 3 (вершины e, f, g класса 2 в хвостах отсутствуют). Следовательно, все восемнадцать цепей, привязанных к вершине a, повторятся в списке из 144 цепей, только головная вершина a окажется уже в хвосте. Аналогичное удвоение произойдет с цепями, привязанными к вершине b, и т.д.

Из 72 цепей куба можно составить один большой цикл, основанный на том же принципе, который заложен в малых циклах, образованных девятью цепями. В 72-цикле в отличие от 9-циклов инверсии подлежат не только хвостовые, но и головные части цепей.