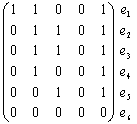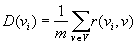Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.2. Морфология графа

Матрицы смежности и инцидентности

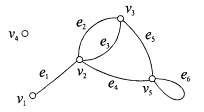
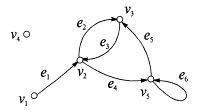
На рис 3.12 изображено множество точек V и множество линий E, соединяющих эти точки, которые все вместе образуют граф Г. Если линии имеют стрелки, то граф называется ориентированным или орграфом Г₀ (рис. 3.13). Внутренних различий между Г и Г₀ гораздо меньше, чем между графом, изображающим правильную решетку из подгрупп для какой-нибудь группы, например,S( ) (рис. 2.18), и графом, изображающим сильно неправильную метарешетку M₁₆ (рис. 2.26).

Рис. 3.12

Рис. 3.13

Внешняя морфология графа (со стрелками или без них) играет подчиненную роль, математическая же сущность представленного графом объекта всегда остается где-то за рамками рисунка. Изображение графа в большинстве случаев является проекцией или тенью этой сущности и самостоятельного значения не имеет. Однако морфология расположения точек и линий, тем не менее, поддается определенной математической классификации и описанию. Этим мы намерены заняться в этом и последующем подразделах.

Линии в графе Г здесь и далее будем называть ребрами, а ориентированные линии в орграфе Г₀ — дугами. О вершинах и ребрах (дугах) говорят, что они инцидентны, если вершина принадлежит ребру (дуге); если вершина не инцидентна никакому ребру (дуге), то она называется изолированной (v₄). Путь называется простым, если никакая дуга или ребро не встречается в нем дважды. Путь называется элементарным, если никакая вершина в нем не встречается дважды.

Цикл — это замкнутый путь в неориентированном графе. Контур — это ориентированный цикл в орграфе. Понятия простоты и элементарности распространяются на циклы и контуры. Контур или цикл, который содержит все ребра или дуги графа, называется эйлеровым. Можно показать, что связанный орграф (т.е. без изолированных фрагментов) содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу выходящих; связанный неориентированный граф содержит эйлеров цикл тогда и только тогда, когда степень каждой вершины четна. Степенью (валентностью) вершины называется число инцидентных ей ребер. Простой путь, который проходит через все вершины графа, называется гамильтоновым. Если в простом графе с n вершинами степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым. Однако легко построить гамильтонов граф, у которого степень вершины меньше n/2.

Графы Г и Г₀ можно представить в аналитической форме либо матрицей смежности A, либо матрицей инцидентности B. Для нашего конкретного неориентированного графа Г матрицы A и B выглядят следующим образом:

A(Г) =	B(Г) =

Матрица смежности для неориентированного графа всегда симметрична. Фигурирующая в ней 2 может быть в некоторых случаях заменена на 1. В матрице инцидентности сумма единиц по столбцам указывает на степень вершины v_i. Нередко расположение вершин и ребер в этой матрице меняют местами (транспонируют). Так, для нашего конкретного орграфа Г₀ матрица A и B выглядят иначе:

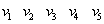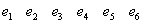A(Г0 ) =	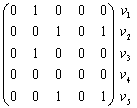B(Г0 ) =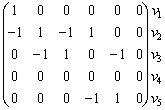

В общем случае матрица смежности для ориентированного графа уже не будет симметричной. В матрице инцидентности ставится 1, если дуга исходит из вершины, и – 1, если дуга заходит в нее.

Число дуг в пути минимальной длины от вершины v_i до v_j называется расстоянием r(v_i, v_j). Если между вершинами не существует никакого пути, то расстояние равно бесконечноти: r(v_i, v_j) = ∞.

Для вершины v_i можно определить среднее отклонение от центра графа:

где m — число дуг в графе Г , v – пробегает вершины V графа Г.

Вершина v₀, для которой эта сумма окажется минимальной, называется центром графа Г. В роли центра могут выступать несколько вершин. Для пересчета возможных путей длины r, рассмотрим различные степени матрицы смежности A(Г₀). Пусть дан орграф Г₀ (рис. 3.14).

Рис. 3.14

A(Г₀) = ,    R = r(i, j) = .

Общее число дуг m = 12; матрица R = r(i, j) отражает расстояние между вершинами; на ее основе рассчитываем всевозможные отклонения: D(1) = D(2) = D(6) = 2/3 — центр графа Г₀, который состоит из трех вершин 1, 2 и 6; остальные отклонения равны: D(3) = 3/4, D(4) = 13/12, D(5) = 11/12.