Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
3.2. Морфология графа
Отношения эквивалентности и порядка
Одна из основных задач, которые решаются по морфологическому анализу ориентированных графов, это разбиение вершин на непересекающиеся классы эквивалентности и порядка. С отношениями эквивалентности и порядка мы сталкивались в теории групп. Оказывается, эти отношения встречаются и в теории графов. Сначала рассмотрим вопрос разбиения вершин Г0 на классы эквивалентности или сильно связанные подграфы.
Введем оператор G, который указывает на связь вершины i с другими вершинами графа Г0. Будем различать две группы G-операторов: прямого Gn(i) действия и обратного G–n(i). Оператор G1(i) указывает на те вершины, в которые можно попасть непосредственно из вершины i; обратный оператор G–1(i) указывает на совокупность вершин, из которых можно попасть в вершину i. Степени G-операторов определяются обычным образом:
G0(i) = {i}, G2(i) = {G1(G1(i))}, G–2(i) = {G–1(G–1(i))}, ...
Непосредственно по рис. 3.30 находим результат действия G-оператора на вершины 1 и 2:
G0(1) = {1}; G–1(1) = {5, 14}; G1(1) = {6, 13};
G–2(1) = {3, 4, 13}; G2(1) = {7, 12, 14};
G0(2) = {2}; G2(2) = {11, 13, 15}; G–2(2) = {3, 15}
G3(1) = {8, 16, 10, 1}; G4(1) = {6, 13, 11, 8, 12, 9};
и т.д. Для всякой вершины i орграфа Г0 можно определить прямое G+(i) и обратное G–(i) транзитивные замыкания. Они определяются через объединение всех степеней G-оператора, соответственно, положительных и отрицательных:
G+(i) = G0(i) ∪ G1(i) ∪ G2(i) ∪ G3(i) ∪ ...
G–(i) = G0(i) ∪ G–1(i) ∪ G–2(i) ∪ G–3(i) ∪ ...
Смысл прямого транзитивного замыкания G+(i) состоит в том, что оно указывает множество вершин орграфа Г0, в которые можно попасть из вершины i. Обратное транзитивное замыкание G–(i) указывает на те вершины Г0, из которых можно попасть в вершину i. В обоих случаях длина пути по числу дуг не ограничивается. Пересечение прямого и обратного замыканий определяет подграф сильно связанных вершин или класс эквивалентности вершины i:
C(i) = G+(i) ∩ G–(i).
Смысл сильной связи заключен в достижимости любой вершины из любой вершины данного класса. Сама вершина i называется представителем класса C(i). В качестве представителя класса эквивалентных вершин может выступать любая вершина этого класса.
Для нашего конкретного орграфа Г0 имеем:
G+(1) = {1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16};
G–(1) = {1, 2, 3, 4, 5, 13, 14, 15}.
Следовательно, первый класс сильно связанных вершин образован тремя вершинами:
C1(1) = G+(1) ∩ G–(1) = {1, 13, 14}.
Вершина 2 попадает во второй класс эквивалентности, где помимо представителя присутствует еще одна вершина — 15-ая:
G+(2) = {2, 11, 15}; G–(2) = {2, 3, 15}; C2(2) = {2, 15}.
Всего подобная процедура позволяет найти восемь непересекающихся классов эквивалентности. Перечислим их без указания вершин-представителей:
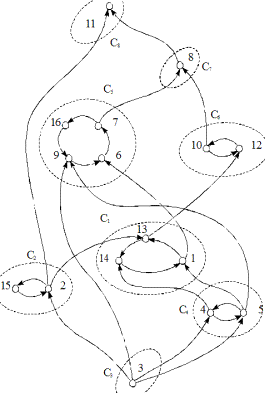
C1 = {1, 13, 14}; C2 = {2, 15}; C3 = {3}; C4 = {4, 5}; C5 = {6, 7, 9, 16}; C6 = {10, 12}; C7 = {8}; C8 = {11}.
Рис. 3.31
Теперь орграф Г0 (рис. 3.30) распался на сильно связанные подграфы, которые подчинены отношению порядка (рис. 3.31). Но прежде, чем приступить к изучению классов порядка, опишем метод нахождения классов эквивалентности при помощи матрицы смежности:
A (Г0) =
Она позволит описанный процесс алгоритмизировать так, чтобы поиск эквивалентных классов можно было осуществить на компьютере. Справа от матрицы A(Г0) размещен столбец прямого транзитивного замыкания, построенного для вершины 1, т.е. G+(1), а под ней строка G–(1).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 * 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 0 * 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 * 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 * 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 2 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 3 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 * 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 3 0 3 2 2 1 * * * * * * * 2 1 4 *Если i = 1, то в клетку столбца против этой вершины ставим нулевую степень. В клетку столбца G+(1) напротив вершины 6 ставим первую степень, так как для первой вершины соответствующая ей строка содержит 1 на позиции 6. Из этих же соображений 1 ставим на 13 месте столбца G+(1). Поскольку строка 6 матрицы A(Г0) содержит 1 в позиции 7, то напротив вершины 7 ставим степень 2. Вместе со строкой 6 рассматривается строка 13; здесь уже две единицы: на позициях 12 и 14; следовательно, в столбце G+(1) на этих местах тоже появляются 2. Это означает, что кратчайшее расстояние от вершины 1 к вершинам 7, 12 и 14 равно двум дугам. Строки 7, 12 и 14 содержат 1 на местах 8, 16, 10 и 1. Из этих четырех чисел последнее отбрасывается, поскольку из вершины 1 мы начали свое движение; соответствующая ей клеточка занята 0. Остальные три числа укажут места, куда выставляется степень 3. Далее, в строках 8, 10 и 16 единицы расположены на 8, 9, 11 и 12 месте; числа 8 и 12 игнорируем, а на 9 и 11 местах столбца G+(1) выставляем 4. Наконец, в строках 9 и 11 мы не находим новых позиций, значит остальные вершины орграфа Г0 из вершины 1 недостижимы. Прямое транзитивное замыкание образовано вершинами {1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16}, как и должно было получиться. В пустых клетках столбца G+(1) выставляем символы « * ».
Аналогичным образом действуем в отношении обратного транзитивного замыкания G–(1), только вместо строк будем рассматривать уже столбцы матрицы смежности A(Г0). Получающиеся числа в строке под матрицей G–(1) являются степенями G-оператора, которые указывают соответствующие длины путей до вершины 1. После проделанной процедуры у нас получается известный набор вершин: {1, 2, 3, 4, 5, 13, 14, 15} с различными степенями достижимости вершины 1.
Удаляя из матрицы A(Г0) общие для G+(1) и G–(1) вершины, т.е. 1, 13, 14, переходим к матрице A'(Г0). В ней выбираем произвольную вершину; пусть ею будет вершина 2. Затем целиком повторяем ту же процедуру, что и над матрицей A(Г0). Так мы находим прямое и обратное транзитивные замыкания для вершины 2, которые были нами уже выписаны. В новой матрице смежности A"(Г0) по сравнению с A'(Г0) отсутствуют позиции 2 и 15. Общее число матриц смежности с последовательно удаленными строками и столбцами равно числу классов эквивалентности; в нашем случае оно равно 8.
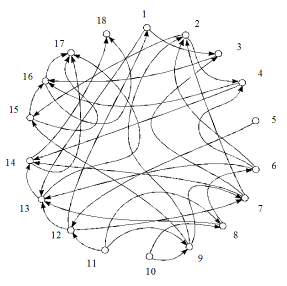
2 3 4 5 6 7 8 9 10 11 12 15 16 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 * 0 0 0 1 0 0 0 0 0 0 0 0 0 * 0 0 1 0 0 0 0 1 0 0 0 0 0 * 0 0 0 0 0 1 0 0 0 0 0 0 0 * 0 0 0 0 0 0 1 0 0 0 0 0 1 * 0 0 0 0 0 0 0 0 0 1 0 0 0 * 0 0 0 0 1 0 0 0 0 0 0 0 0 * 0 0 0 0 0 0 1 0 0 0 1 0 0 * 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 * 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 * 0 1 * * * * * * * * * 1 *3 4 5 6 7 8 9 10 11 12 16 0 1 1 0 0 0 1 0 0 0 0 * 0 0 1 0 0 0 0 0 0 0 0 * 0 1 0 0 0 0 1 0 0 0 0 * 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 0 0 0 0 0 3 0 0 0 0 0 1 0 0 0 1 0 * 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 1 0 0 0 * 0 0 0 0 0 0 1 0 0 0 0 2 2 3 2 0 3 * 1 * * * 2 3 4 5 8 10 11 12 0 1 1 0 0 0 0 * 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 * 0 0 0 1 0 0 1 * 0 0 0 0 0 0 0 * 0 0 0 0 1 0 0 * 1 0 1 * * * *Разбиению на классы порядка поддаются только те орграфы, которые не содержат контуров и петель. Если таковые имеются, то прежде необходимо произвести разбивку на классы эквивалентности, а затем каждый из классов принять за вершину нового орграфа. В нашем случае этот новый орграф будет содержать восемь вершин, причем их упорядочение из рис. 3.31 вполне очевидно. Чтобы не играть с читателем в поддавки, возьмем в качестве исходного орграфа Г0, подлежащего упорядочению, более сложную структуру на 18 вершинах, изображенную на рис. 3.32; здесь уже иерархию вершин предугадать сложно.
Рис. 3.32
Упорядочение по матрице смежности A(Г0) производится строго по столбцам. Если упорядочение производить по строкам, то полученная иерархия будет соответствовать противоположному направлению дуг. Мы приводим оба вида упорядочения, чтобы продемонстрировать их различие. Когда спрашивается, изменится ли разбиение вершин на классы порядка при одновременной смене направления всех дуг орграфа Г0 (рис. 3.32), обычно отвечают: «нет, классы останутся прежними». Но это не так; упорядочение по противоположным направлениям дуг, т.е. по строкам матрицы смежности A(Г0), создает другие классы порядка.
Итак, опишем прямое разложение орграфа на классы порядка по столбцам матрицы A(Г0). Для нахождения первого класса порядка C1 подсчитаем число единиц в каждом столбце и выпишем результаты в первую строку под матрицей A(Г0). В трех позициях, а именно: 5, 10 и 11, оказались нули, так как в соответствующих столбцах отсутствуют единицы. Это означает, что вершины 5, 10 и 11 образовали самый нижний уровень; им не предшествует ни одна дуга; они являются «истоками»; эти три вершины образовали класс C1 .
A (Г0) =
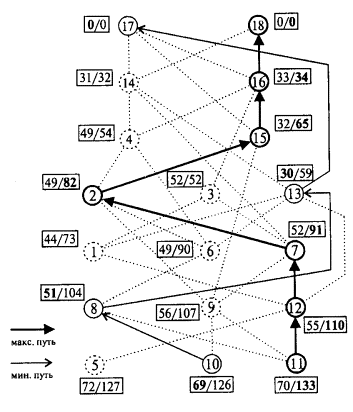
Далее, мысленно (чтобы не выписывать новую матрицу смежности) вычеркнем из матрицы A(Г0) названные строки и вновь подсчитаем число единиц по столбцам, а результат запишем во вторую строку под матрицей; на местах же 5, 10 и 11 выставим символы « * ». Во второй строке нули окажутся в 8, 9 и 12 позициях, значит, вершины под этими номерами образуют класс C2. Снова вычеркиваем три строки, соответствующие уже этим вершинам. Начинаем искать вершины третьего класса C3 и т.д. В результате получим семь классов порядка. На рис. 3.33 изображен упорядоченный орграф Г0, разложенный на семь классов порядка Ci , которым отвечают семь уровней.
Рис. 3.33
Обратное разложение орграфа на классы порядка по строкам матрицы A(Г0), которое будет соответствовать противоположному направлению дуг, по количеству тоже дает семь классов, но по составу вершин три из них отличаются от прямого разложения. Выпишем для сравнения все классы порядка, причем классы разложения по противоположному направлению дуг пометим штрихом:
C1 = C1' = {5, 10, 11}, C2 = C2' = {8, 9, 12},
C3 = {1, 6, 7}, C3' = {6, 7}, C4 = {2, 3, 13}, C4' = {1, 2},
C5 = {4, 15}, C5' = {3, 4, 13, 15},
C6 = C6' = {14, 16}, C7 = C7' = {17, 18}.
Если бы на каком-то этапе появилась строка (для прямого разложения) или столбец (для обратного разложения) без нулей, то это означало бы, что исходный орграф Г0 содержит контуры и требуется предварительная процедура разложения Г0 на подграфы сильно связанных вершин. У нас такой ситуации не возникло.