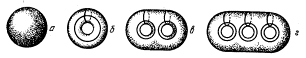Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.5. Раскраска графов и вопросы топологии

«Кренделя» и странные свойства гептаэдра

На рис. 3.75, наряду с шаром (а) и тором (б), показаны «кренделя» с двумя (в) и тремя (г) отверстиями. На изображенных телах проведено минимальное число разрезов, сохраняющих целостность поверхности. На шаре никаких замкнутых линий нет, на торе их число равно двум, на кренделе с двумя отверстиями их четыре, на кренделе с тремя отверстиями их пять и т.д. Следовательно, для шара σ = 1, для тора σ = 3, для кренделя с двумя отверстиями σ = 5, для кренделя с тремя отверстиями σ = 7 и т.д. Связанность данных топологических поверхностей равняется нечетному числу. А как получить четные значения связанности? Может быть, попробовать просверлить дырки в поверхностях, как это показано на рис. 3.76?

Рис. 3.75

Рис. 3.76

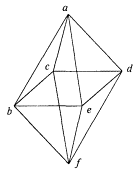
Действительно, в этом случае связанность поверхностей можно изменить; для изображенных тел с дырками величина связанности будет равна следующим значениям: а) σ = 2, б) σ = 3, в) σ = 7, г) σ = 8. В связи с наличием у поверхности одной или несколько дырок, определение первой разрезающей линии должно измениться. Теперь и она не может быть замкнутой; первая разрезающая линия должна начинаться и заканчиваться на границах дырки. Проведя на поверхности сферы разрез от одной дырки к другой, мы тем самым не нарушим целостности его поверхности, значит, величина связанности геометрической формы (а) равна двум. Единственная дырка, проделанная на поверхности тора (б), не меняет его связанности. Две дырки, просверленные на кренделе с тремя отверстиями (г), увеличили связанность на единицу, а добавление трех дырок к кренделю с двумя отверстиями (в) добавило две единицы связанности. Таким образом, чтобы рассчитать связанность поверхности (σ') с h дырками, нужно определить связанность ее без дырок (σ), а затем добавить к найденной величине число h – 1, т.е.σ' = σ + h – 1.

Поверхность с σ = 2 можно сконструировать и по-другому. Если взять октаэдр (рис. 3.77), провести внутри него три плоскости по ребрам: acfe, abfd, bcde, удалить четыре грани: abc, ade, bef, cdf, то в итоге получим тело, которое называется гептаэдром, т.е. многогранник с семью гранями. Он имеет следующие параметры: n = 6, m = 12, f = 7. Из формулы Эйлера для гептаэдра находим:

σ = m – n – f + 3 = 12 – 6 – 7 + 3 = 2.

Рис. 3.77

Здесь требует пояснений число ребер. Дело в том, что диагонали октаэдра для гептаэдра не образуют ребер. Если бы пересечение плоскостей acfe, abfd, bcde давало дополнительные элементы: n = 7, m = 18, f = 16, то это противоречило бы определению многогранника, а по формуле Эйлера получили бы σ = – 2, что не имеет никакого топологического смысла. Теперь более внимательно присмотримся к свойствам гептаэдра.

Предположим, что на внешней стороне грани abc, в самом ее центре сидит жук. Он начинает ползти к середине ребра ac, движется по квадратной грани acfe, доползает до середины ребра fe, движется по внешней, т.е. развернутой к нам, стороне грани bfe, пересекает середину ребра bf, ползет по квадрату abfd, достигает середины ребра ab и, наконец, преодолевая финишную прямую, перемещается к центру грани abc, но, как оказалось, уже с внутренней стороны.

Таким образом, гептаэдр обладает всеми свойствами петли Мёбиуса, которая изображена на рис. 3.68. Как мы помним, эта скрученная на 180 градусов лента имеет одну неориентированную поверхность, которую нужно разрезать дважды, чтобы она распалась на две несвязанные области. Первый разрез должен быть замкнутым; его необходимо сделать от точки Q до точки Q' по указанному на рисунке пути. В результате получим петлю в два раза большего диаметра и перекрученную уже не на 180 градусов, а на все 360. Второй разрез тоже не нарушает связанности и только третий разрез, сделанный от края до края, разделит ленту на две части. Следовательно, петля Мёбиуса имеет σ = 2. 

Сфера с двумя дырками (рис. 3.76а), имеющая величину связанности, равную двум, тем не менее, не обладает свойствами петли Мёбиуса, так как ее поверхность имеет две стороны, которые можно выкрасить в два различных цвета. Неориентированные поверхности, которые имеет петля Мёбиуса и гептаэдр, выкрашиваются только в один цвет, как если бы они имели у поверхности одну-единственную сторону. Кажется, что гептаэдр имеет внутренние пустоты, отделенные гранями от внешнего пространства. Но это обманчивое впечатление: неориентированные или односторонние поверхности не способны делить общее пространство на внутреннюю и внешнюю области.