Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.5. Раскраска графов и вопросы топологии

Бутылка Клейна и вывернутые поверхности

Шесть вершин гептаэдра представляют собой особые точки, которых нет на петле Мёбиуса. Но скрученная и склеенная лента — это даже не поверхность, а только половинка ее и полное отсутствие какой-либо объемности. Спрашивается, существует ли нечто наподобие петли Мёбиуса, но более объемной конструкции? Да, ответил Феликс Клейн и предложил вниманию математиков топологическое тело в виде бутылки, которая сейчас носит его имя (рис. 3.78). Нетрудно догадаться, что связанность этой поверхности совпадает со связанностью тора, так как, разрезав бутылку Клейна по любой окружности малого диаметра, мы получим цилиндр переменного радиуса; далее можно делать разрез вдоль продольных линий цилиндра; отсюда и берется величина σ = 3. Но если тор имеет внутреннюю область, отделенную от внешней стенками тора, т.е. ориентированную поверхность, то бутылка Клейна этим свойством не обладает.

.

Рис. 3.78

Бутылка Клейна, петля Мёбиуса и гептаэдр — это готовые статические конструкции с вывернутыми поверхностями. В XX в. топологи начали ставить задачи динамического характера и одной из первых была задача по выворачиванию сферы наизнанку. Сфера, в отличие от названных фигур, имеет ориентированную поверхность, внутреннюю сторону которой можно выкрасить в синий, а внешнюю — в красный цвета. Если после такой покраски северный и южный полюса сферы поменять местами, двигая их вдоль оси, соединяющей эти полюса, то сфера окажется вывернутой наизнанку таким образом, что внешняя ее сторона станет синей, а внутренняя — красной. При этом по всей окружности экватора образуется складка. Когда полюса пройдут большую часть своего пути вдоль оси и внешний цвет сферы изменится с красного на синий, по всей длине экватора возникнет тороидальная поверхность, выкрашенная с внешней стороны еще в красный цвет (рис. 3.79а). Таким образом, наполовину вывернутая сфера демонстрирует нам еще один интересный топологический эффект, когда внешнее и внутреннее пространства как бы переплетаются, поскольку снаружи оказываются одновременно и красная, и синяя стороны поверхности. Отсюда также видно, какую важную роль играет для топологии раскраска поверхностей.

a) 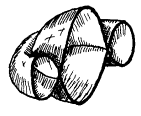б) в)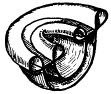

Рис. 3.79

По мере того, как операция по выворачиванию сферы будет подходить к концу, малый радиус окружности экваториального тора устремится к нулю, пока тор совсем не исчезнет. Однако исчезновение складки означает, что вблизи экватора поверхность сферы испытала высочайшее напряжение, которое в предельном случае приведет к ее разрыву. Ситуацию разрыва поверхности можно смоделировать на проволоке. Если петлю на проволоке максимально затянуть, проволока не выдержит и порвется. Аналогичное явление произойдет вдоль всей линии экватора. Топологами был поставлен вопрос: можно ли сферу путем непрерывных преобразований ее поверхности вывернуть так, чтобы избежать разрыва? Оказалось, что можно; ряд теорем, доказанных Стивеном Смейлом (1959), Арнольдом Шапиро (1979) и Тэруо Нагасэ (1984) доказали это. Идея состоит в том, чтобы, не доводя дело до разрыва, создать на поверхности несколько складок, которые можно было бы перекатывать по поверхности, деформируя ее различным способами. Образование таких складок в виде шляпы и шляпы с подкладкой показаны на рис. 3.79 б и в. Задача имеет несколько решений, которые зависят от характера складок. На рисунке 3.80а показаны складки, захватывающие и переворачивающие часть поверхности сферы или другого тела. Разумеется, подвергать процедуре выворачивания можно не только сферу, но и тор, кренделя и прочие ориентированные и неориентированные поверхности. На рис. 3.80б показан разрез тора, который содержит внутри себя несколько тороидальных областей, о пространстве которых невозможно сказать, являются ли они продолжением внешнего пространства или образуют свое самостоятельное.

a) 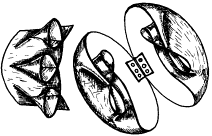б)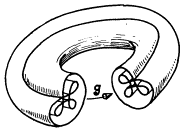

Рис. 3.80

Граф — это во многом объект топологии; проблема раскраски графа продемонстрировала нам взаимозависимость теории графов и топологии. Но существует третья абстрактная теория, которая примыкает к обеим упомянутым — это теория узлов и зацеплений.