Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
4.10. Аттракторы от функции косинуса
Функция ax cos(x) представляет собой простую косинусоиду, амплитуда которой монотонно увеличивается с ростом аргумента x. Однако высшие моды от этой рекурсивной функции представляют собой сложный математический объект. В предпринятом далее анализе фрактальная природа мод этой тригонометрической функции выдвигается на первый план.
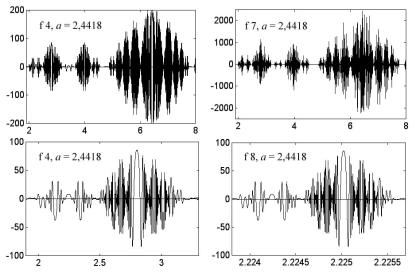
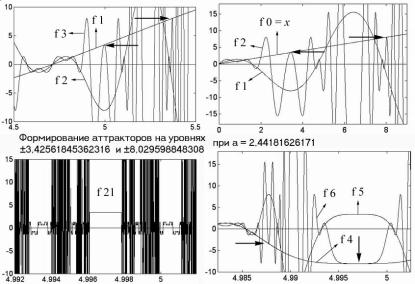
Рис. 4.45
Рассмотрите внимательно рис. 4.45, состоящий из четырех окон, где прекрасно виден фрактальный характер приведенных там мод. На двух верхних графиках даны моды f 4 и f 7 при одном и том же значении a = 2,4418 и на одном и том же отрезке оси абсцисс, только значения ординат для f 7 почти в 10 раз больше, чем для f 4. Два нижних графика иллюстрируют абсолютное равенство амплитуд двух мод f 4 и f 8, но обратите внимание на ось абсцисс: мода f 8 сжата по оси x почти на три порядка по сравнению с модой f 4.
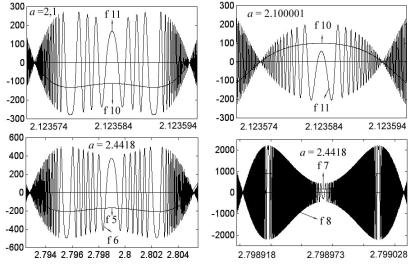
Рис. 4.46
Рис. 4.46 демонстрирует модуляционные свойства мод: там, где первая производная предыдущей моды меняет знак на противоположный, происходит смена фазы колебаний и последующей моды, так что локальные максимумы мод f 10 и f 11 совпадают. Именно на экстремумах, как мы убедимся ниже, быстрее всего развиваются шумовые процессы, но там же возникают и аттракторы, которые противодействуют хаосу. Два верхних графика показывают чувствительность мод к величине коэффициента a: изменение его значения на одну стотысячную радикально меняет внешний вид моды. Поэтому в определенных случаях, чтобы показать некоторые тонкие эффекты, например прокол аттрактора, величину коэффициента a приходится указывать с точностью до 15 знака после запятой.
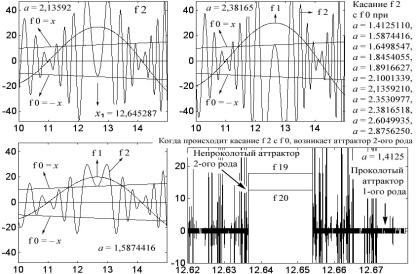
Рис. 4.47
Аттрактор возникает прежде всего в месте касания положительной или отрицательной диагонали, которую мы договорились обозначать через f 0 = ± x, с той или иной модой. В частности, на рис. 4.47 показаны три различные фазы касания f 2 с модой f 0, которым отвечают и различные значения коэффициента a. Поскольку данный аттрактор находится в области x1 = 12,65, то один из двух аттракторных уровней, соответствующий четным модам, равен 12,65; другой аттракторный уровень для нечетных мод будет меняться в зависимости от коэффициента a. В табл. 4.8 приведены десять значений коэффициента a и соответствующие им значения второго аттракторного уровня. Если этот аттракторный уровень принять за координату x, то в данной точке x при том же коэффициенте a обнаружится аттрактор, одним из значений которого будет 12,65. Таким образом, уровни аттрактора указывают на области оси абсцисс, где происходит касание характеристических экстремумов моды f 2 с прямыми f 0.
Таблица 4.8
a x 1,412510 17,805 1,587420 20,011 1,649850 20,798 1,891660 23,846 2,100130 26,474 2,135920 26,925 2,353097 29,663 2,381651 30,022 2,604993 32,838 2,875625 36,250 В нижнем правом окне рис. 4.47 указанные аттракторы имеют вид двух прямых, отвечающих четным и нечетным модам, в частности, f 19 и f 20, полученным при а = 1,4125. Коэффициент а может меняться в узких или широких пределах. В табл. 4.8 приведены значения коэффициентов, когда аттракторы существуют для всех высших мод. На самом же рис. 4.47 приведены значения коэффициента, когда появляются первые признаки разрушения аттрактора (в этом случае говорят о его проколе). Добавим также, что в табл. 4.8 значения координаты x, где расположен второй аттрактор, даны приблизительно и вот почему. Эти значения иногда очень точны; например, при а = 1,58742 для всех высших мод, для которых все переходные процессы уже улеглись, значение второго уровня равно 20,01089998094886 при x1 = 12,65. Аналогичная картина наблюдается при коэффициенте а = 2,10013, когда второе значение равно неизменному значению 26,47409436146688. Но иногда значение второго уровня заметно «гуляет», как, например, при коэффициентах а = 1,41251 и а = 2,381651. Нередко вместо двух значений появляется четыре: два уровня с положительными знаками и два примерно таких же значения, но уже с отрицательными знаками. Подобная картина наблюдается, в частности, при коэффициентах а = 1,64985, а = 2,13592 и а = 2,3530977.
Ниже все эти отклонения получат надлежащее объяснение, а пока нам надо хорошо усвоить, что аттракторный уровень указывает на значение оси абсцисс, где нужно искать аттрактор, отвечающий этому же значению. Если аттрактор состоит из четырех уровней, значит, в четырех указанных точках оси абсцисс находятся аттракторы с такими же уровнями. Два уровня для четных и нечетных мод возникают потому, что рассмотренный нами аттрактор в области x1 = 12,65 принадлежит второму роду. Род аттрактора определяется порядком моды и ее касательной. Все аттракторы второго рода образуются при сечении вершины моды f (n + 2) модой f n. Уже говорилось, что аттракторы могут появиться и в тех местах оси x, на которые уровни непосредственно и не указывают. Например, аттрактор второго рода может появиться в том месте оси абсцисс, где мода f 1 слегка отсекает вершину моды f 3.
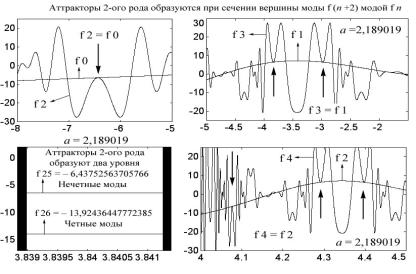
Рис. 4.48
Такую ситуацию можно наблюдать на рис. 4.48, где запечатлены моменты соприкосновения мод f 3 с f 1, а также f 2 с f 0 и f 4 с f 2 (точки нахождения аттракторов второго рода указаны большими стрелками). Во всех случаях разность порядков дает число 2, что и определяет род аттрактора. Сам аттрактор второго рода показан в левом нижнем углу рис. 4.48 при коэффициенте a = 2,189019 в области x = 3,84, хотя два аттракторных уровня равны совершенно другим значениям, а именно: f 25 = –6,4 и f 26 = –13, 9. По графикам f 3 и f 4 легко обнаруживается фрактальная природа данных мод, которые различаются лишь степенью сжатости по оси абсцисс. Тот факт, что не только прямая f 0, но и любая высшая мода f n может выполнять роль касательной и секущей для f (n + 2), а также создавать точки притяжения и обеспечивать устойчивость аттрактора, является главным смыслом этого рисунка.
У читателя может сложиться ложное представление, будто аттракторы второго и высших родов мы строим сами. Всё выглядит ровно наоборот: рассматривая бесконечные «гирлянды» мод в общем-то однотипного строения, вы вдруг натыкаетесь на абсолютно инородное образование в виде очень узкого или, напротив, достаточно широкого «плато», где все моды принимают одно, два или несколько дискретных значений относительно небольшой величины. Чтобы понять, откуда оно там взялось, почему оно имеет такие, а не иные количественные характеристики, вы и начинаете интересоваться его предысторией, пристально всматриваетесь в сплетение низших мод и пытаетесь установить соответствие между величиной отсечения низшими модами «макушки» у высших мод, с одной стороны, и шириной плато, с другой. Таким образом, ваш творческий труд похож на исследовательскую работу геолога-разведчика, который месяцами кружит по унылому горному ландшафту и вдруг среди бесформенных валунов пустой породы находит драгоценный кристалл удивительно правильной формы и необычайной красоты. Геолог, естественно, попытается установить его строение и происхождение, для чего составит подробное описание находки и той местности, где она была обнаружена. Настойчивость, внимательность, аккуратность сделают свое дело и вы всегда добьетесь успеха в изучении никому неизвестных объектов, которые повсюду окружают нас.
Рис. 4.49
Рис. 4.49 был включен в книгу потому, что он дает ясное представление о схожести графического «ландшафта», на котором появляются аттракторы. По сравнению с предыдущими рисунками, здесь приведены три моды: две смежные моды образуют аттракторы первого рода, уровни которых не достигают и полуторной величины от единицы, а моды, образующие аттрактор второго рода, дают неизменную и легко узнаваемую конфигурацию, которая повторяется при любых масштабах. Обратите внимание на расположение пиков в трех из четырех окнах, где отображены триады: f 0, f 1, f 2; f 1, f 2, f 3; f 4, f 5, f 6. Правый верхний рисунок в точности повторяет левый верхний, что обеспечивает идентичность аттракторов на уровнях +3 и +8 (местонахождение их указано большими стрелками). На правом верхнем рисунке нет и намека на присутствие аттрактора в районе x = 5. Этот математический факт открывается лишь на левом верхнем рисунке, где видно, как третья мода соприкасается с первой, но и там аттрактора второго рода, как такового, еще не существует. Он появляется лишь на правом нижнем рисунке вместе с четвертой модой, которая и «просела» под аттрактором на уровне –8. Мода f 6 очертила границы аттрактора для четных мод, а мода f 5 — для нечетных. Правый нижний рисунок сильно искажен под действиями сил притяжения аттрактора второго рода, однако и в нем прекрасно сохранена общая композиция расположения пиков. Левый нижний рисунок с модой f 21 демонстрирует уже вполне сформировавшиеся аттракторы первого рода в форме «Крепостной стены» и второго рода в виде двух дискретных уровней, куда притягиваются все высшие моды, но о которых ничего еще «не знали» низшие моды.
Теперь нужно хорошо запомнить следующее: то, что говорится и показывается на модах в пределах, скажем, первого десятка или даже первой сотни номеров, будет наблюдаться и тогда, когда порядок мод перевалит через сотню или миллиард. Всё упирается в микроскопичность пространств, которых «боится» человек и машина, но которых «не страшится» бестелесная математика. С ростом порядка моды, число аттракторов первого, второго и прочих родов увеличивается, так что на них натыкаешься чуть ли не в каждой точке оси абсцисс, хотя их протяженность быстро укорачивается. Однако не следует удивляться тому, что беря, к примеру, моду f 1000 и желая измерить ее амплитуду в произвольно выбранной точке x, вы обнаруживайте, что она принимает одно из значений дискретного уровня аттрактора первого рода (он встречается чаще других).
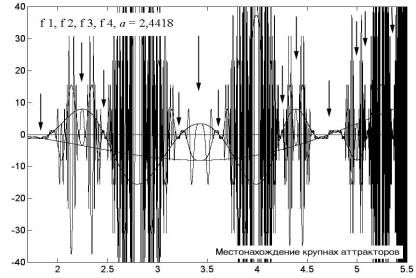
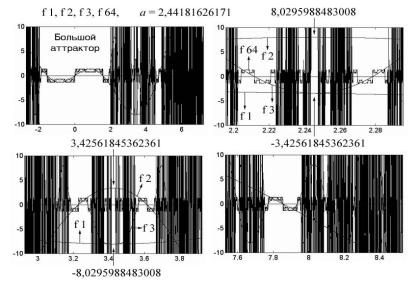
Рассмотрите внимательно рис. 4.50, где хорошо видны «завязи» крупных аттракторов первого и второго рода (на них указывают большие стрелки). Аналогичная картина будет появляться на высших модах при малой длине волны. Мы выбрали для определенности коэффициент а = 2,44181626171 и на следующем рисунке (рис. 4.51) проследили поведение моды f 64. Как видно из четырех графиков, ее ход во многом предопределен первыми тремя модами. Постройте свои собственные графики при других коэффициентах a, которые бы давали несколько отличную картину распределения аттракторов первого и второго рода, попробуйте установить общие закономерности и элементы симметрии. Так называемый Большой аттрактор, простирающийся от –2 до +2, и несколько самых широких просветов задаются «соединением» и «оппозицией» мод f 1, f 2 и f 3. Аттракторы от высших мод, в том числе и от моды f 64, при таких масштабах просто не будут видны.
Рис. 4.50
Изучая тонкую структуру аттракторов, удобно, наряду с высшими модами, в качестве ориентира приводить и моды первых порядков. Когда на экран дисплея выводится картинка одной какой-нибудь высшей моды, всегда приходишь в изумление: откуда ей «знать», где нужно оставить просвет и тянуться горизонтальной линией в виде аттрактора, а где быстро колебаться с амплитудой, уходящей вниз и вверх от нулевого уровня на сотни миллиардов единиц? Но если наряду с высшей модой показаны кривые низших мод, то к вам приходит понимание того, что высшие моды «помнят» о низших и «руководствуются» информацией, полученной от своих предшественниц.
Рис. 4.51
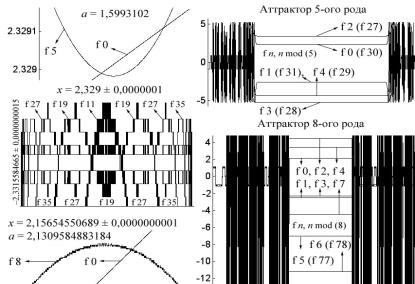
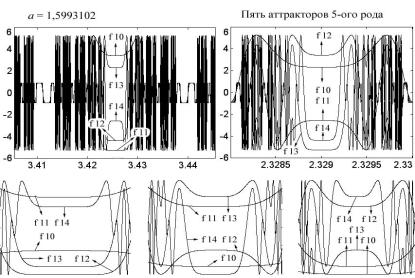
Рис. 4.52 знакомит читателя с аттракторами пятого и восьмого рода функции ax cos(x). Как и в случае с аттракторами второго рода, их параметры всецело определяются сечением «макушки», соответственно, от мод f 5 и f 8 диагональю f 0. Чтобы в этом убедиться самим, нужно подставить указанный коэффициент a и координату x в соответствующий рекурсивный цикл. На этом и последующих рисунках координаты области изображения, например моды f 5, указываются следующим образом:
x = 2,329 ± 0,0000001.
Эту запись следует понимать так: середина экрана дисплея или отдельного рабочего окна отвечает точке x = 2,329; левая и правая границы экрана или окна отличаются от указанного значения на величину 0,0000001 (или, при другой записи, 0.1е – 6) в меньшую и большую стороны, соответственно. Если был бы указан только плюс:
x = 2,329 + 0,0000001,
то число 2,329 определило бы левую границу, а число 2,3290001 правую границу всего экрана или отдельно взятого окна. Аналогичная система обозначений действует и в отношении ординаты, только левая и правая границы заменяются на нижнюю и верхнюю. Это — технические детали, но без них не воспроизвести графики.
Рис. 4.52
На восьмой моде видны следы шума, который проявил себя и на уровнях тонкой структуры аттрактора. В центральной части аттрактора на уровни –2,33, занятой модами f 11 и f 19, заметны характерные шумовые уширения импульсных фронтов. Однако вопросы шума и тонкого строения аттрактора мы оставим на будущее, а пока сосредоточимся на общем строении аттракторов.
Каждый уровень аттрактора пятого рода образует класс мод, порядок которых дает один и тот же остаток их деления на число 5. Так, наш аттрактор пятого рода построен на пяти модах с f 27 по f 31, которые и дали пять уровней (напомним, род аттрактора совпадает с числом уровней). Следующая мода f 32 в области действия аттрактора совпадет с модой f 27, образующей первый верхний уровень; мода f 33 займет самый нижний уровень, прочерченный модой f 28, и т.д. Таким образом, каждый уровень отбирает класс мод с номером f n, где n = {0, 1, 2, 3, 4} по mod (5). То же самое происходит и в отношении восьми уровней аттрактора восьмого рода. Здесь номера мод даются в остатках от деления порядка моды на число 8. Например, под модой f 5 могут оказаться следующие моды: f 77, f 85, f 93 и т.д.;
f 6 = {..., f 54, f 62, f 70, f 78, f 86, f 94, ...}.
Рис. 4.53
На рис. 4.52 показаны аттракторы вполне сформировавшиеся; однако любопытно посмотреть, как они появляются, для чего необходимо обратиться к модам низшего порядка. На рис. 4.53 и 4.54, где показаны два полных комплекта аттракторов пятого и восьмого рода, такая возможность предоставлена. В левом верхнем окне рис. 4.53 показан аттрактор в районе x = 3,425, который отвечает первому верхнему уровню, впервые прочерченному модой f 10 (пик моды f 5, отсекаемый диагональю f 0, еще не образует аттрактора). В правом верхнем окне этого же рисунка показан аттрактор в районе x = 2,329, отвечающий второму верхнему уровню, который также впервые был прочерчен модой f 10. По меткам оси абсцисс можно сказать, что ширина этого аттрактора примерно в 10 раз меньше ширины предыдущего. Три нижних аттрактора, показанные уже вне рамок координатной системы, отвечают трем оставшимся уровням, расположенным в отрицательной области. Десятая мода последовательно занимает положение от самого верхнего до самого нижнего уровня. Как и в случае с аттракторами второго рода, отыскать комплект аттракторов пятого рода не составит большого труда, если найден один из них. Для этого нужно только величину аттракторных уровней подставлять в значения координаты x. В силу симметрии функции косинуса, точно такие же аттракторы будут находиться в зонах –x. Новые комплекты аттракторов пятого рода при этом же коэффициенте (a ≈ 1,6) появятся в местах отсечения макушек мод f 6 модами f 1 (обозначим эти зоны как f 1/f 6), затем в местах f 2/f 7, f 3/f 8 и т.д. до фрактальной бесконечности.
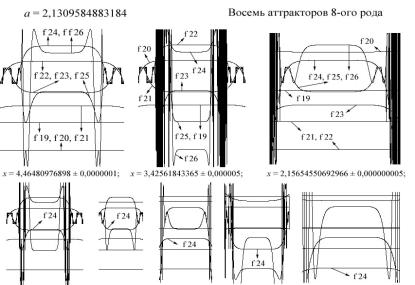
Рис. 4.54
Все сказанное в отношении аттрактора пятого рода распространяется и на аттрактор восьмого рода. Здесь роль моды f 10 взяла на себя мода f 24 (вторая после f 16, если брать номер моды по mod (8)), которая прочертила данный уровень для всех последующих высших мод порядка f 0. На аттракторах первого и второго рода можно наблюдать взаимодействие уровней: их удержание на определенной высоте происходит за счет «взаимодействия» четных или нечетных мод. Для аттракторов 3-, 4-, 5-го и высших родов взаимодействие между уровнями усложняется: моды делятся не только на четные и нечетные, но группируются по mod (3), mod (4), mod (5) и т.д. При рассмотрении тонкой организации аттракторных уровней мы остановимся на этом вопросе более подробно, но уже сейчас хочется обратить внимание читателей на сплетение мод f 22, f 23 и f 24 (см. верхний левый рис. 4.54), образующие по бокам аттрактора восьмого рода два симметрично расположенных аттрактора первого рода. Трехуровневое взаимодействие от мод f 22, f 23 и f 24 аттрактора, расположенного в районе x = 4,46, передалось модам f 20, f 21 и f 22 аттрактора, находящегося в зоне x = 3,42; в области x = 2,15 эту эстафету приняли на себя моды f 24, f 25 и f 26. Излишне, наверно, говорить, что подобные механизмы «завязи» аттракторов действуют не только в отношении тригонометрических функций, но также и других рекурсивных функций, включая закон Ферхюльста и экспоненциальный закон.
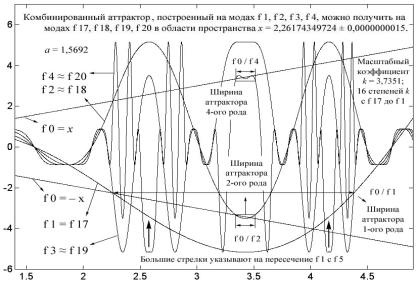
Обратите внимание, что рассмотренный выше аттрактор пятого рода является, собственно, подсистемой более широкого аттрактора, который существует при этом же коэффициенте (a ≈ 1,6) и который «подстриг» все видимые в двух верхних окнах рис. 4.53 амплитуды мод таким образом, что они не выходят за пределы ±6. Большой комбинированный аттрактор, определенный двумя диагоналями f 0 и первыми четырьмя модами, изображен на рис. 4.55. Здесь мы видим, что аттрактор первого рода, простирающийся примерно от 2,2 до 4,4, поглотил множество перекрывающихся аттракторов второго (f 0/f 2) и четвертого рода (f 0/f 4) в районе x = 3,42. Очевидно, что в широкий аттрактор первого рода попадут также два боковых аттрактора четвертого рода типа f 1/f 5, на которые указывают две большие стрелки. Далее эта ситуация будет повторяться нескончаемое число раз на высших модах.
Рис. 4.55
Читатель может полюбоваться точно такой же картинкой, какая была получена на модах f 1 — f 4, но уже воссозданной при участии мод f 17 — f 20, если уменьшит масштаб изображения в k 16 раз, где k = 3,7351, т.е. около 1,5 млрд. раз. Фрактальная природа рекурсивной функции ax cos(x) здесь проявляет себя в полной мере. Однако не потому, что размерность выражается дробным числом, а потому, что имеет место масштабная инвариантность изображения. (Вообще говоря, k — не число, т.е. величина не постоянная; она заметно колеблется от моды к моде; дается же среднее значение k.) Данная аттракторная композиция способна репродуцировать себя в сколь угодно малых масштабах. Приобретя на больших модах прямоугольные черты, каждый дискретный импульс, т.е. крохотная частица этого сложного строения, содержит в сжатом виде всю конструкцию в целом. Вещь поразительная и достойная вашего самого пристального внимания. Масштабную инвариантность как таковую, проявляющуюся в изоморфизме мод, которую мы обозначили символом подобия (≈), можно наблюдать повсеместно (на это уже обращалось внимание); здесь же удивляет композиционная сложность сохраняемых форм аттрактор