Конструктивная математика

Акимов О.Е.

15. Конструктивная алгебра

Основная заслуга европейских математиков до Ньютона состояла в том, что они конструктивным методом проб и ошибок продолжили исследовать все многообразие решений различных алгебраических уравнений, которые впервые начали составлять и детально исследовать арабские математики. Путь был длинным и тернистым, а продвижение по нему очень медленным и долгим. Никто из математиков не может похвастаться тем, что он без единомышленников, живших до него или в одно время с ним, единолично создал теорию решения алгебраических уравнений; каждый из прославленных математиков вносил лишь крупицу драгоценных знаний.

Это касается Ньютона, пожалуй, в большей степени, чем кого бы то ни было. Свой лекционный курс под названием «Всеобщая арифметика» он читал в Кембридже с 1673 по 1683 гг. В нем он рассмотрел 77 задач, из которых 61 были геометрического характера и только 16 арифметического. В основу своих лекций британский ученый, по всей видимости, положил многочисленные исследования европейских математиков, плененных алгебраическими приемами, найденными арабами, труды которых в настоящее время нам не известны. В качестве непосредственного образца он взял «Геометрию» Декарта, хотя ссылок на нее он практически не делал. Так, он сформулировал правило знаков для определения числа положительных и отрицательных корней алгебраического уравнения, но оставил его без обоснования. У французского же ученого он позаимствовал не только методику и математическую символику, в частности, извлечение корней и обозначение степеней неизвестного, но и решение некоторых конкретных задач. В общем, заслуги Ньютона перед алгеброй, которую он называл всеобщей арифметикой, были более чем скромные, хотя времени на нее он затратил неизмеримо больше, чем на свои флюксии.

Арабские сочинения по математике получили хождение в Европе еще в эпоху крестовых походов менее образованных христиан против более образованных мусульман. На закате Средневековой эпохи наиболее распространенной книгой по математике была «Краткая книга» аль-Хорезми в переводе Фибоначчи. Леонардо Фибоначчи занимался в основном практической математикой и прославился «Книгой счета» (1202), служившей пособием для бухгалтеров и купцов (первые 14 чисел Фибоначчи были приведены в трактате 1228 г.). Много позже, в 1494 г., выходит «Сумма арифметики, геометрии, учения о пропорциях и отношениях» Луки Пачоли (1445—1515) — друга и единомышленника Леонардо да Винчи. Этот фундаментальный труд имел в своем составе специальный отдел (IX), состоящий из двенадцати трактатов, посвященных коммерческим вопросам: о товариществах (I), об аренде (II), о менах и меновых сделках (III), ..., о мерах, весах и монетах (XII). Но главное его достоинство было все же в другом. Немалая часть его объема составила теория и практика решений алгебраических уравнений и теоретическая геометрия. Пачоли рассматривал решения уравнений второй и некоторые виды четвертой степени, причем старался находить только положительные корни, поскольку не признавал отрицательных чисел и ноль. Что же касается кубических уравнений, то возможность их решение он вообще отвергал.

Однако прежде чем мы станем рассказывать об успехах европейских математиков, нужно коснуться того, что было сделано арабскими. Ранее было показано, что математика эллинов во многом носила малопродуктивный и формальный характер, связанный с сильнейшим влиянием на нее софистической силлогистики элеатов и, главным образом, Аристотеля. Никто не отрицает великие достижения в этой области Фалеса, Пифагора, Демокрита, Евдокса, Архимеда, Аполлония, Гиппарха и Птолемея. Однако 13 книг евклидовых «Начал», помимо явных математических успехов, демонстрируют еще и скрытые пружины гибели науки эллинов. Ясно, что однажды провозглашенная система аксиом ставит препоны творческим исканиям конструктивно думающих людей. Реконструкция египетских и вавилонских задач, предложенные, в частности, Раик, Розиным и другими исследователями, наводят на мысль, что конструктивная методика, связанная с конкретными геометрическими построениями, не была целиком изобретением греков, более того, она скорее всего была перенята ими вместе с алгоритмами египтян и вавилонян. Такой вывод невозможно сейчас строго доказать на основе письменных документов, которые до нас попросту не дошли, но он вытекает с высокой степенью вероятности из генетической несовместимости общей идеологии конструктивизма и формализма.

Софисты, эти учителя красноречия и показушной мудрости, вроде Протагора, расцветшие в «золотой век» Перикла, внесли в школьные программы эллинов элементы пустого формализма. Почему мы и говорим, что «Начала» Евклида нужно считать не только памятником высочайших достижений математических наук Древности, но и началом их заката. Софистическая логика резко контрастировала с наглядными пространственными образами, хотя и была совместима с логикой построения алгоритмических вычислений. На этой почве и появился знаменитый аксиоматический метод эллинов, который явился результатом приложения логики элеатов к алгоритмам вавилонян и египтян.

Софистическая школа диктовала, чтобы отправные понятия и положения размещались вначале излагаемого предмета. Эта понятная, с дидактической точки зрения, процедура затем была канонизирована и воспета софистами как единственно допустимая форма научного мышления. Высокие формалистские и низкие геометрические способности софистов как раз и демонстрируют приведенные нами доказательства формулы квадрата суммы и теоремы Пифагора, взятые в качестве примера из «Начал» Евклида. Логика и геометрия, конечно, присутствовали в рассуждениях вавилонян и египтян, но они выступали у них в естественном и как бы свернутом виде. Чтобы усвоить накопленные ими математические знания, греки препарировали и широко развернули их в плоскости логики и геометрии. Эти два отнюдь не новых инструмента интеллектуальной деятельности человека в процессе усвоения чужих знаний закалялись и оттачивались. Позже с их помощью грекам удалось продвинуться далеко вперед и заметно обогнать своих учителей. Известно, что вавилоняне умели решать многие виды квадратных уравнений, а у греков сохранился нетривиальный алгоритм и геометрическая интерпретация для нахождения неизвестной величины x квадратного уравнения двух видов:

b² = ax + x² = (a + x)x = (a/2 + x)² – a²/4 и
b² = ax – x² = (a – x)x = (a/2 – x)² – a²/4,

первое уравнение называлось гиперболическим (что означает с избытком), второе — эллиптическим (т.е. с недостатком). Для нахождения искомой величины x по гиперболическому уравнению греки вычерчивали отрезок AC (рис. 9а), равный a, и строили на стороне AD прямоугольник, равный по площади b². Сторона AD превышала AC на искомую величину x, а точка B делила отрезок AC пополам. Аналогично решалось эллиптическое уравнение.

Но, в общем, греки не слишком далеко ушли от достижений вавилонян и египтян в решении уравнений именно по причине неумения как следует пользоваться геометрическими методами. Зато достаточным конструктивным потенциалом обладал ум арабов. Первым среди математиков багдадской школы стоит имя прославленного Мухаммеда ибн Муса аль-Хорезми, т.е. Мухаммеда, сына Мусы, из Хорезма. Хорезма — древнее неисламское государство, впоследствии завоеванное мусульманами.

Слово аль-Хорезма послужило прототипом для слова алгоритм — правила. Это произошло потому, что самое популярное математическое сочинение арабов «Краткая книга об исчислении аль-джабара и аль-мукабалы», принадлежавшее перу аль-Хорезми, в начале XIII в. было переведено Леонардо Пизанским (1180—1250), сыном купца Боначчи, также известного нам под именем Фибоначчи. В своем трактате аль-Хорезми ввел два правила: аль-джабар и аль-мукабала. От первого слова берет свое начало слово алгебра, так как подобные правила по существу сформировали новую отрасль математики.

  

     

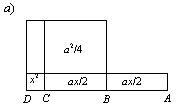
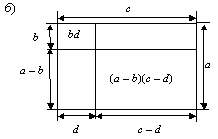
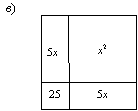
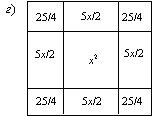
Рис. 9

Слово аль-джабар переводится как восстановление; правило позволяет восстанавливать положительное число из отрицательного, что давала процедура переноса отдельных членов уравнения вправо или влево за знак равенства. Например, уравнение 3x² = 2 – 5x, с помощью правила аль-джабар, записывалось как 3x² + 5x = 2. За счет этого правила, арабы стали воспринимать символ « – » как отрицательный знак перед числовым значением. Для отрицательных чисел они сформулировали четыре правила, одно из которых звучало так: враг моего врага мне друг (минус на минус дает плюс). 

Греки не воспринимали отрицательных чисел, так как были уверены, что из ничего (нуля) невозможно отнять положительное число, хотя еще от вавилонян они переняли правило действия с разностями отрезков:

(a – b)(c – d) = ac – ad – bc + bd,

которое иллюстрировалось соответствующим чертежом (рис. 9б). Глядя на формальное выражение, можно подумать, что греки умели обращаться с отрицательными числами, однако минус они воспринимали как операцию вычитания меньшей величины из большей. 

Правило аль-мукабала позволяло приводить подобные члены, в частности, уравнение 3x² – x² + 10x – 2x = 6 благодаря этому правилу превращалось в уравнение 2x² + 8x = 6. Аль-Хорезми на основе указанных алгебраических правил сводил разнообразные квадратные уравнение к одному из пяти видов: 

ax² = bx, ax² = c, ax² + bx = c, bx + c = ax², ax² + c = bx,

для которых были разработаны конкретные алгоритмы решения. Квадрат искомой величины часто брался без коэффициента a, так что, например, последнее уравнение сводилось к x² + q = px. Алгоритмическая запись решения последнего уравнения отвечала формулам:

и ,

но всегда приводилась для конкретного числового уравнения.

Приведем текст, соответствующий нахождению неизвестного x, удовлетворяющего уравнению x² + 21 = 10x: «Раздвой корни, это будет пять, и умножь это на равное себе, будет двадцать пять, и вычти из этого двадцать один, которые прибавлены к квадрату, остается четыре, извлеки из этого корень, будет два, и вычти это из половины корней, т.е. пяти, остается три; это и будет корень квадрата, который ты ищешь, а квадрат есть девять. А если хочешь прибавить это к половине корней, будет семь, и это есть корень квадрата, который ты ищешь, а квадрат есть сорок девять» [31, c. 195]. 

Под словосочетанием «раздвой корни» понималась операция деления коэффициента при x на два, т.е. p/2 = 10/2. Данный текст мало чем отличается от аналогичных алгоритмических текстов, встречающихся на египетских папирусах и глиняных табличках вавилонян. Это и понятно, если учесть, что арабы использовали ту же самую конструктивную методологию, что и древние математики. Отличие заключалось лишь в том, что далее в трактате аль-Хорезми давался совет по проверке результатов поиска корня x с помощью чертежа, изображенного на рис. 9в, в соответствии с формулой:

x² + 2(p/2)x + (p/2)² = q + (p/2)².

Египтяне же и вавилоняне не слишком заботились о проверке решения задач и не стремились приводить чертежи, позволявшие им найти алгоритмы. Последнее связано также с тем, что египтяне и вавилоняне располагали более примитивными средствами для воспроизведения информации, чем арабы. Поэтому не исключено, что египтяне и вавилоняне учили на словах аналогично арабом, только не писали об этом. Поскольку греки времен Евклида и схоласты практически не открывали новых формул, то все их математические выкладки свелись к проверке, т.е. к подтверждению того, что не ими полученные выражения действительно верны.

Несомненно, у аль-Хорезми геометрические построения шли впереди уравнений, что видно из следующих рассуждений. Дополнив прежний чертеж (рис. 9в) так, как это показано на рис. 9г, он вывел алгоритм решения аналогичного уравнения вида: x² + 10x = 39. В самом деле, построив квадрат x² и добавив к нему четыре прямоугольника с высотой p/4 = 10/4 и четыре маленьких квадрата площадью 25/4, можно определить площадь большого квадрата:

q + 4(p/4)² = (x + 2p/4)² = 64. 

Следовательно, сторона этого квадрата равна 8, а искомая величина x = 3, поскольку x = – p/2. Впрочем, шел ли сначала чертеж, а потом уравнение, или наоборот, не столь уж важно. Главное, что арабы с использованием геометрии, в конце концов, научились решать квадратные уравнения самого общего вида.

Более того, Сабит ибн Корра (836—901), который перевел на арабский язык некоторые труды Аполлония, Архимеда и Евклида, формулируя архимедову задачу о сечении шара плоскостью, самостоятельно пришел к уравнению третьей степени: x³ + q = px, которое послужило затем толчком для исследования кубических уравнений. 

Аль-Бируни (973—1050), решая задачу о нахождении стороны правильного вписанного в круг девятиугольника, свел ее к двум кубическим уравнениям: x³ + 1 = 3x и x³ = 1 + 3x (для них было найдено приближенное решение). К первому уравнению можно свести и задачу о трисекции угла. В самом деле, известно, что sin 3φ = 3sinφ – 4sin³φ; положим, что 3φ = 2π/3; тогда sin 3φ = 1/2 и 1 = 6sinφ – 8sin³φ; если далее положить 2sinφ = x, мы как раз и придем к уравнению 1 = 3x – x³. 

Решая задачу по разделению числа 10 на две части так, чтобы сумма их квадратов от деления большей части на меньшую равнялась 72, Абу-л-Джуд пришел к уравнению x³ + 27x/2 + 5 = 10x², для которого нашел один корень x = 2. То, что число корней должно быть равно степени уравнения, арабы не знали; эта истина открылась позднее европейцам (строгое обоснование этому математическому факту дал Декарт).

Поэт и ученый Омар Хайям (1048—1131) написал трактат по алгебраическим уравнениям, где привел их классификацию, состоящую из 25 видов, 14 из которых были кубические. Его классификация не была известна европейским математикам Нового времени. Впервые трактат был обнаружен и опубликован на арабском языке лишь в 1936 г. Тем не менее этот трактат говорит нам сейчас об уровне развития арабской математики XI—XII вв. В нем автор приводит методы решения уравнений и дает определение того, что нужно понимать под алгебраическими вычислениями. Хайям пишет: «Алгебраические вычисления производятся с помощью уравнений; как хорошо известно, уравнение — это уравнивание одних степеней другими».

Большинство кубических уравнений Хайям решает с помощью пересечения прямых и окружностей с линиями конических сечений. Так, корни уравнения x³ + a = bx, он ищет на пересечениях параболы x² = yb^1/2 и гиперболы x² – ax/b = y²; корни уравнения x³ + bx = cx² + a он определят с помощью окружности y² = (x – a/b)(c – x) и гиперболы x(b^1/2 – y) = a/b^1/2. Разумеется, все алгебраические уравнения имели у него конкретный числовой вид. Например, для уравнения x³ + 41² = 80x² им было найдено два корня: x = 41, x = 41 + 39(3/4) и т.д. 

Таким образом, нынешнюю во многом символьную алгебру арабы сформировали как методику сведения конкретных прикладных задач к одному или нескольким уравнениям различной степени и нахождению одного или двух корней с помощью конкретных геометрических построений. Декарт, создавая свою аналитическую геометрию, во многом опирался на алгебраические работы арабов, которые вырастали из синтетической геометрии греков.

На алгебраическом трактате Хайяма развитие арабской математики, конечно, не закончилось. После него некий анонимный автор привел геометрическое построение для нахождения одного из корней уравнения четвертой степени вида x⁴ + 2000x = 20x³ + 1900. В трактате самаркандского математика аль-Каши (XIV—XV вв.) «Ключ арифметики» дается классификация, состоящая из 65 видов уравнений, и методы решения, в том числе, уравнений четвертой степени. 

Помимо алгебраических уравнений, перевода и комментирования греческих авторов, арабы интересовались вычислениями корней. Ими были получены любопытные соотношения, например, такие:

,  ,   ,

,  

и т.д. К этим числовым равенствам приводили всё те же геометрические и алгебраические приемы, которые давали и более общие выражения, в частности, такое:

.

Весьма похожую формулу приводит и Ньютон в своей «Всеобщей арифметике»:

,

которая затем вошла во все европейские учебники алгебры. Таким образом, основным достижением математиков стран ислама было создание алгебраической науки, конструктивный дух которой мусульмане передали первым ученым возрожденной Европы.

В 1508 г. Пачоли издал Евклида с длинным названием на титульном листе: «Сочинение мегерянина Евклида, тончайшего философа и по справедливости первого из всех математиков, переведенные достойным внимания Компано. Сочинения эти по вине издателя были настолько искажены ошибками, что едва ли в них можно узнать Евклида. Лука Пачоли, заслуженный теолог, сей высший и редчайший между математическими науками предмет по своему разумению исправил и издал». Вскоре вышла еще одна книга Пачоли, иллюстрированная рисунками Леонардо да Винчи, со столь же характерным по длинноте названием: «Божественная пропорция. Книга весьма полезная всякому проницательному и жаждущему знания уму, из которой каждый занимающийся философией, перспективой, живописью, скульптурой, архитектурой, музыкой или другими математическими предметами, может приобрести приятные, остроумные и удивительно достойные сведения и найти развлечения по различным вопросам и самым тайным знаниям». Помимо изложения вопросов, связанных так или иначе с «золотой пропорцией», будоражащей воображение гуманистов эпохи Ренессанса, в книге рассказывалось о Платоновых телах, архитектуре и многих других предметах, часто очень отдаленных от математики.

На книгах Пачоли воспиталась целая плеяда итальянских математиков: Ферро, Тарталья, Бомбелли и, конечно же, Джироламо Кардано (1501—1576). К этому времени Европа, и особенно Италия, были наводнены математической литературой (с 1472 по 1500 гг. было отпечатано 214 различных сочинений по математике). Пачоли знал Кардано-отца, который был известным юристом, но его книги все же больше приковали внимание Кардано-сына. В «Сумме» Пачоли имелась задача следующего содержания: «Два игрока поставили по 105 ливров с условием, что общий выигрыш достанется тому, кто первым выиграет три партии. Но после того как первый игрок выиграл две партии, а второй – одну, игра неожиданно прервалась. Вопрос: как разделить 210 ливров, стоящих на кону, между игроками?» Пачоли предлагал разделить всю сумму 2 : 1, т.е. первому отдать 140, второму – 70 ливров. Джироламо Кардано, известный также как большой любитель азартных игр, позволил себе не согласиться с мнением признанного авторитета. Он обратил внимание на то, что первому игроку осталась выиграть только одну партию, а второму – две, т.е. шансы первого на окончательную победу предпочтительней, чем у второго. И хотя эту задачу Кардано не сумел довести до конца (ее решили Ферма и Паскаль: первый игрок должен получить 157,5 ливра, второй – 52,5), его критика представленного в «Сумме» решения была вполне справедливой. Добавим к сказанному: данная задача имела ключевое значение для становления теории вероятности.

Прославился же Кардано книгой «Великое искусство, или О правилах алгебры», которую в 1545 г. подготовил к печати Оссиандер, издавший до этого, в 1542 г., знаменитый труд Николая Коперника «Об обращении небесных сфер». В «Великом искусстве» дается общая методика решения кубического уравнения x³ + ax² + bx + c = 0, которое через замену x = y – a/3 сводится к уравнению без квадратного члена. 

Действительно, указанная подстановка дает уравнение вида y³ + py + q = 0, где p = b – a²/3, q = 2a³/27 – ab/3 + c. Неполное же кубическое уравнение сводится к квадратному. В самом деле, подстановка y = u + v приводит к уравнению u³ + v³ + (3uv + p)(u + v) + q = 0. Если принять, что uv = – p/3, то в последнем уравнении можно избавиться от члена u + v, обратив его в уравнение u³ + v³ = –q. Далее принимаем кубы u³ и v³ за корни квадратного уравнения z² + qz – p³/27 = 0, т.е. считаем, что y = u + v = + . Последнее выражение и образует так называемую формулу Кардано.

Сейчас для общего решения требуется добавить еще два комплексно сопряженных корня:

y = – (u + v)/2 ± i(u + v) /2,

которые у Кардано не фигурировали. Даже отрицательные корни он называл фальшивыми. Следует также заметить, что исследование кубических уравнений итальянский математик проводил на числовых примерах; не все соотношения, которые могут существовать между коэффициентами кубического уравнения, он рассмотрел полностью и, что самое важно, уравнения вида x³ + ax = b, x³ + b = ax и x³ = b + ax до него умел решать Тарталья и Ферро. Не станем сейчас рассказывать, о сути конфликта, вспыхнувшего на этой почве между математиками; скажем лишь, что Кардано, несмотря на элементы заимствования, провел большую самостоятельную работу, заслуживающую самой высокой оценки.

Случай, когда коэффициенты неполного кубического уравнения удовлетворяют условию (p/3)³ > (q/2)², приводящему к мнимым корням, рассмотрел Рафаэль Бомбелли (1526 – 1573). Число в его записи означало 2i, а выражение = 4 + i. Действия с комплексными корнями у него отвечали принятым сейчас операциям с мнимой единицей: i² = – 1 и (– i) · i = 1. Так, для уравнения x³ = 15x + 4 он нашел следующее решение:

x = + , понимая, что

· = 5.

Дальнейшее заметное продвижение в поиске решений кубических уравнений сделал французский математик Франсуа Виет (1540 – 1603). Это произошло благодаря усовершенствованию символики, в частности, им была введена буквенная система обозначения корней и коэффициентов, что сразу же дало известное правило Виета в виде двух простых формул для квадратного уравнения:

p = – (x₁ + x₂) и q = x₁x₂;

для кубического уравнение

x³ + ax² + bx + c = 0

три коэффициенты выражались следующими равенствами:

a = – (x₁ + x₂ + x₃), b = x₁x₂ + x₂x₃ + x₃x₁, c = – x₁x₂x₃.

Подобные формулы позволили Виету провести более качественный анализ уравнений первых четырех порядков (подстановки, сводящие уравнения 4-ой степени к уравнению 3-ей степени, были представлены уже в «Великом искусстве» Кардано). Заслуги французского математика перед наукой огромны; он дал формулы разложения тригонометрических функций sin nφ и cos nφ через степени sin φ и cos φ. Это достигалось с помощью выведенных им рекуррентных соотношений:

cos nφ = 2cos φ cos (n – 1)φ – cos (n – 2)φ,
sin nφ = 2cos φ sin (n – 1)φ – sin (n – 2)φ.

Он также разложил число π в бесконечное произведение косинусов:

π/2 = cos π/4 · cos π/8 · cos π/16 · cos π/32 · ...

и сделал много других полезных вещей в области математики.

Дело Виета достойно продолжил другой французский мыслитель — Рене Декарт (1596—1650). Декарт, а за ним Ньютон и все остальные математики, сводил уравнения к виду, который впоследствии стали называть каноническим, т.е. когда слева от равенства писался ноль. Декарт догадался, что число корней должно равняться наивысшей степени неизвестного, ибо, говорил он, перемножение n линейных двучленов вида (x – c), где c – корень, только и может дать наивысшую степень xⁿ. 

Об этом он писал в следующих словах: «Всякое уравнение может иметь столько же различных корней или же значений неизвестной величины, сколько последняя имеет измерений; ибо если, например, принять x равным 2, или же x – 2 равным ничему, а также x = 3 или же x – 3 = 0, то, перемножив оба эти уравнения x – 2 = 0 и x – 3 = 0, мы получим xx – 5x + 6 = 0, или же xx = 5x + 6, уравнение, в котором величина x имеет значение 2 и вместе с тем значение 3. Если принять еще, что x – 4 = 0 и умножить это выражение на xx – 5x + 6 = 0, то мы получим x³ – 9xx + 26x – 24 = 0, другое уравнение, в котором x, обладая тремя измерениями, имеет вместе с тем три значения, а именно 2, 3 и 4» [32, c. 369 – 370]. 

Понимание алгебраических уравнений в Европе установилось в точности такое же, какое оно было в странах исламского мира. Определение его у Ньютона, которое мы находим во «Всеобщей арифметике», повторяет приведенное нами выше определение Хайяма. Схоластический формализм Евклида и Аристотеля сгубил математику и физику, затормозил развитие науки вообще более чем на полторы тысячи лет. Сбросив ярмо формальной логики, арабы эпохи Средневековья и европейцы Нового времени, опираясь на образные представления, двинули всю мировую науку вперед.