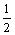
Конструктивная математика
Акимов О.Е.
18. Как избавиться от расхождения
К исключительно формально-логическим рассуждениям, по-видимому, можно было бы отнести доказательства монаха из Пизы Гвидо Гранди (1671—1742), который считал, что сумма знакочередующихся единиц равна 1/2:
1 – 1 + 1 – 1 + 1 – 1 + ... = 1/2,
так как, рассуждал монах, собирая скобки в одном порядке, мы получим 1, а собирая их в другом порядке — 0:
1 – (1 – 1) – (1 – 1) – (1 – 1) – ... = 1,
(1 – 1) + (1 – 1) + (1 – 1) + ... = 0;
значит, заключил этот исследователь, истина находится посередине, т.е. результат равен 1/2. Примерно такую же дедуктивную цепочку выстраивал Эйлер в отношении другого ряда:
1 – 3 + 5 – 7 + 9 – 11 + ... = 0.
Между тем, сумма ряда Гранди постоянно колеблется: при нечетном числе членов она равна 1, при четном — 0. В ряде Эйлера сумма по своей абсолютной величине равномерно растет, но тоже колеблется между положительным и отрицательными значениями:
1, – 2, 3, – 4, 5, – 6, 7, – 8, ... .
Поэтому в современной математике ряды Гранди и Эйлера с легким сердцем зачислили в расходящиеся, а для всех расходящихся рядов принят символ бесконечности ∞.
Два последних примера свидетельствуют о существовании зависимости суммы ряда от числа его членов. В ранее приведенных примерах эта зависимость, очевидно, тоже существовала, но она была совершенно иной природы, чем в двух последних случаях. Похоже, что в рядах Гранди и Эйлера проблемы возникли из-за неоправданной экстраполяции представлений о бесконечных рядах с непрерывно убывающими (вплоть до полного их исчезновения) членами на знакопеременные ряды.
Итак, все знакопеременные ряды имеют «колеблющуюся» сумму, зависящую от числа членов, но будут ли они все расходящимися? Нет, конечно; существуют хорошо известные разложения, которые «расходящимися» никак не назовешь. Например:
sin x = x – x3/3! + x5/5! – x7/7! + ...,
cos x = 1 – x2/2! + x4/4! – x6/6! + ...
Следовательно, вопрос состоит не в том, как назвать ряд — сходящимся или расходящимся, а как определить его сумму. Эту проблему отчетливо понимал Эйлер. «И вот я говорю, — писал он, — что вся трудность кроется в названии "сумма". Действительно, если под "суммой" ряда понимать, как это обычно делается, результат сложения всех членов, то нет никакого сомнения, что суммы можно получить только для тех бесконечных рядов, которые являются сходящимися и дают результаты, тем более близкие к некоторому определенному значению, чем больше членов складывается. Расходящиеся же ряды, члены которых не убывают ..., вообще не будут иметь никаких определенных сумм, если только слово "сумма" понимается как результат сложения всех членов. Этих затруднений и кажущихся противоречий мы совершенно избежим, если припишем слову "сумма" значение, отличное от обычного. А именно, мы скажем, что сумма всякого ряда есть значение того конечного выражения, из развертывания которого возникает этот ряд. При этом соглашении, если ряд будет сходящимся, то новое определение слова "сумма" совпадает с обычным, а так как расходящиеся ряды не имеют никакой суммы в собственном смысле слова, то из этого нового определения не проистечет никаких неудобств. Приняв это определение, мы сможем сохранить выгоды пользования расходящимися рядами и в то же время защититься от всяческих обвинений» [37, с. 101].
В связи с пониманием суммы ряда, как некоего «конечного», компактно свернутого выражения, которое при определенной процедуре можно было бы развернуть в бесконечный ряд, возникает задача нахождения условий для существования такой единообразной процедуры для всех возможных рядов. Почему, собственно, одни ряды могут иметь такие компактные выражения (сходящиеся ряды), другие не могут (расходящиеся ряды)? Не будут ли эти самые расходящиеся ряды иметь свои вполне конечные выражения, которые, однако, мы еще не научились отыскивать? Может быть, эта новая процедура или принятие каких-то новых условий прояснит нам ту непонятную пока разницу в «суммах» для вполне сопоставимых членов, как то:
1/1 + 1/2 + 1/3 + ... = ∞, (1/1)2 + (1/2)2 + (1/3)2 + ... = π2/6,
и какую из двух сумм признать верной для ряда Гранди —
эту: 1 – 1 + 1 – 1 + 1 – 1 + ... = ∞
или эту: 1 – 1 + 1 – 1 + 1 – 1 + ... = 1/2?
В пользу последней «суммы» как будто бы говорит элементарное разложение в ряд Тейлора следующей функции
1/(1 + x) = 1 – x + x2 – x3 + ...
при подстановке x = 1 мы получаем ряд Гранди с конечной суммой, равной 1/2. Но в традиционной математике как раз принято, что для значения x = 1 указанное разложение почему-то недействительно. Для значения x = 0,99999999... оно еще работает, а вот для x = 1 перестает работать. Если бы последнее условие было справедливым, то все знакопеременные ряды вида
(1 + 1)–2 = 1 – 2 + 3 – ... = 1/4,
(1 + 1)–3 = 1 – 3 + 6 – 10 + ... = 1/8
и т.д. имели бы конечные суммы, однако этих конечных значений нынешние математики не признают. Всё это для конструктивного ума кажется странным.
Таким образом, дотошный исследователь природы математических объектов скажет вам, что с бесконечными рядами дело обстоит не самым лучшим образом. Символ бесконечности ∞ играет роль фигового листка: его выставляют всякий раз там, где возникают какие-нибудь сложности в нахождении суммы бесконечных рядов, хотя ясно, что природа возникающих трудностей совершенно различна. Поэтому весьма желательно, в том числе и с формально-логической точки зрения, чтобы суммы рассматриваемых рядов не зависели от перестановки мест слагаемых и чтобы эти суммы имели единообразную процедуру нахождения. Понятно, что все ряды оказались поделенными на два класса: в первый попали ряды с конечной «суммой», во второй — с неопределенной, но отнюдь не бесконечной. Эта граница, как свидетельствуют графики, изображенные на рис. 15, и в табл. 13 сейчас проходит где-то по гармоническому ряду.
На первый взгляд кажется, что понимание «суммы», предложенное Эйлером, и вычислительная процедура, предложенная Тейлором, в состоянии нам помочь, так как многие «расходящиеся» ряды она делает вполне «сходящимися». Однако остается под сомнением понятие о местоположении членов ряда. Как можно терпеть положение, когда обыкновенная перегруппировка членов одного и того же ряда с «суммой», равной ln2, в одном случае дает число (1/2)ln2, а в другом — (3/2)ln2?
Действительно, пусть ранее «расходящимся» рядам теперь будут присвоены конечные «суммы» в соответствии с некоторыми вычислительными процедурами, в частности, для ряда Гранди 1/2, поскольку
1/(1 + x) = 1 – x + x2 – ...,
при x = 1 имеем 1 – 1 + 1 – ... = 1/(1 + 1).
Аналогично:
1/(1 + 1)2 = 1 – 2 + 3 – ... = 1/4,
1/(1 + 1)3 = 1 – 3 + 6 – ... = 1/8
и т.д. Так как разложение
1/(1 – 2x) = 1 + 2x + 4x2 + 8x3 + ...
при x = 1 имеет следующий вид
1 + 2 + 4 + 8 + ...,
то «сумма» последнего ряда равна –1. Такой результат на первый взгляд представляется весьма необычным. Возможно, поэтому математики решили приписать этому ряду «сумму», равную ∞, — она выглядит более логичной.
Вычислительные процедуры, отличные от разложения Тейлора, могут приводить к иным результатам, согласно которым, например, разложение
1/(1 – x) = 1 + x + x2 + x3 + ... = –1/2,
хотя при x = 1 дробь 1/(1 – x) = ∞, что опять же лучше согласуется с «суммой» ряда 1 + 1 + 1 + ... Аналогичная процедура в качестве «суммы» натурального ряда даст значение, равное –1/12.
Предположим, что указанные «суммы» бесконечных рядов справедливы, т.е.
1 + 1 + 1 + ... = –1/2 , 1 + 2 + 3 + ... = –1/12,
тогда имеем:
2 + 4 + 6 + ... = 2(1 + 2 + 3 + ...) = 2(–1/12) = –1/6,
1 + 3 + 5 + ... = 2 + 4 + 6 + ... – (1 + 1 + 1 + ...) = –1/6 + 1/2 = 1/3,
1 + 2 + 3 + ... = (1 + 3 + 5 + ...) + (2 + 4 + 6 + ...) = 1/3 – 1/6 = 1/6,
1 – 2 + 3 – ... = (1 + 3 + 5 + ...) – (2 + 4 + 6 + ...) = 1/3 + 1/6 = 1/2.
Между тем, выше уже было принято, что 1 + 2 + 3 + ... = –1/12, а не 1/6 и что ряд 1/(1 + 1)2 = 1 – 2 + 3 – ... = 1/4, а не 1/2. О подобных проблемах говорили многие, в том числе и Харди [38], откуда были взяты последние выкладки.
Разложение tgx и ctgx ничем особенным не отличается от разложения двух других тригонометрических функций sinx и cosx, выписанных выше; они равны:
tgx = x + x3/3 + 2x5/15 + 17x7/315 + ...,
ctgx = 1/x – x/3 – x3/45 – 2x5/945 – ...,
Однако Яков Бернулли (1654—1705) в своих астрономических исследованиях пришел к несколько иным разложениям. Например, ряд ctgx у него выглядел так:
(x/2)ctg(x/2) = 1 – B1x2/2! – B2x4/4! – ... – Bnx2n/(2n)!
Математик Муавр коэффициенты Bn назвал числами Бернулли, которые оказались равными следующим значениям:
B1 = 1/6, B2 = 1/30, B3 = 1/42, B4 = 1/30,
B5 = 5/66, B6 = 691/2730, B7 = 7/6, ...
С помощью этих чисел Бернулли определял «суммы» рядов типа 1k + 2k + 3k + ... Впоследствии Эйлер пользовался так называемыми числами Эйлера, определенным образом связанными с числами Бернулли, но имеющими целочисленное значение:
E1 = 1, E2 = 5, E3 = 61, E4 = 1385,
E5 = 50521, E6 = 2702765, E7 = 199360981, ...
Числа Бернулли и Эйлера весьма часто встречаются в числовом анализе. Оба математика глубоко проникли в существо проблемы. Высказывание Эйлера о том, что «каждый ряд должен обладать определенным значением», по-видимому, основывалось на понятии Якова Бернулли об остаточном члене ряда. В связи с этим понятием он писал:
«... Нельзя вообще писать l/(n + m) = l/m – ln/m2 + ln2/m3 – ... (*), забывая о последнем бесконечно удаленном члене, который равен (–1)plnp/mp(n + m). Только когда он бесконечно мал, имея в виду исчезновение бесконечно малого перед конечным, можно писать (*). Во всех других случаях, например, при m = n, в конце следует писать не просто многоточие, а этот член:
1/2m = 1/m – 1/m + ... ±1/2m или 1/2 = 1 – 1 + 1 – ... (–1)n/2,
что, конечно, уже верно» [39, с. 271].
Если учесть остаточный член ряда δ, о котором говорил Бернулли, то неоднозначности в сложении и вычитании рядов можно избежать. В самом деле, имеем
1 + 2 + 3 + ... = (1 + 3 + 5 + ...) + (2 + 4 + 6 + ...) + δ = 1/3 – 1/6 – 1/4 = –1/12,
1 – 2 + 3 – ... = (1 + 3 + 5 + ...) – (2 + 4 + 6 + ...) + δ = 1/3 + 1/6 – 1/4 = –1/4,
где δ =
(n) = –1/4, что отвечает вышеприведенным значениям.
Тем не менее, даже с учетом остаточных членов, при нахождении одних и тех же «сумм» различными вычислительными методами, которые вполне работоспособны в других случаях, часто возникает неоднозначность. Чтобы напрочь исключить ее, приходится прибегать к более радикальным мерам. И здесь следует вспомнить, что при становлении европейской науки, когда еще не улеглись споры о необходимости введения отрицательных чисел (древние греки с ними дело не имели), Декарт, а за ним Ньютон и другие математики, приняли следующий хорошо нам знакомый числовой порядок:
– ∞ , ..., – 3, – 2, – 1, 0, + 1, + 2, + 3, ..., + ∞.
Сейчас он стал общепринятым, как говорится, «для всех случаев жизни». Однако уже Эйлер и многие его последователи, менее известные математики, думали совершенно иначе. Они считали, что переход от положительных чисел к отрицательным может происходить не через нейтральный ноль, как сейчас это принято, а через ± ∞, т.е. имеет место совершенно иное упорядочение чисел:
+ 0, + 1, + 2, + 3, ..., + ∞, – ∞, ..., – 3, – 2, – 1, – 0.
Основное отличие между первой и второй числовыми последовательностями состоит в том, что в первой, ныне принятой последовательности, предполагается наличие только одного нулевого числа, который не имеет знака, что достаточно некорректно, поскольку имеем два бесконечных числа (± ∞), отсюда:
и
.
Следовательно, должно быть и два различных нулевых числа, каждый со своим знаком: чисел без знака просто не должно существовать. Вторая числовая последовательность позволяет окончательно снять проблему расходящихся радов; для нее все ряды будут сходиться к некоторым конечным числам единообразной природы, которая, однако, отличается от природы особых чисел ± ∞. Например, бесконечные арифметические прогрессии оказываются равны следующим дробям:
1 + 1 + 1 + ... = – 1/2
1 + 2 + 3 + 4 + ... = – 1/12,
1 + 3 + 5 + 7 + ... = 1/3 и т.д.
На этот счет имеется достаточно простой алгоритм: сумма членов любой бесконечной арифметической прогрессии a1, a2, a3, ... an, ... , где an = a1 + (n – 1)d и d ³ 0, равна (5d – 6a1)/12. В наших предыдущих примерах a1 = 1, а d = 0, 1, 2, и т.д. Чтобы понять, почему это так, нужно обратиться к книге Р.Р. Варшамова [40].
Однако читатель должен отдавать себе отчет в том, что с новым упорядочением числового ряда традиционная математика не ставится с ног на голову, так как необычная эйлерова последовательность целых чисел только и нужна, чтобы корректным образом свертывать бесконечные ряды. Можно сказать по-другому: чтобы математически корректно разворачивать такие функции как 1/(1 – x), ctgx и ln(1 + x), необходимо перейти на несколько иное упорядочение чисел. Подобная реорганизация числового ряда является типичной конструктивной мерой, которую формалисты непременно обойдут стороной, предпочитая ввести в лексикон ряд новых терминов, вроде «условной сходимости» и т.д.
В разделе «Действия с 0,1-матрицами» курса «Дискретная математика» [4, с. 130] была сконструирована иная числовая ось, а именно: всем элементам традиционной последовательности
... , – 3, – 2, – 1, 0, + 1, + 2, + 3, ...
были поставлены в соответствие матрицы размерности 2 ´ 2:
...,
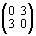 ,
,
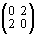 ,
,
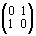 ,
,
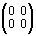 ,
,
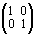 ,
,
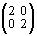 ,
,
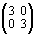 , ...
, ...
Тогда сложению чисел будут отвечать действия над матрицами:
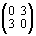 +
+
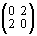 =
=
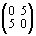 ,
,
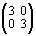 +
+
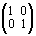 =
=
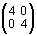 ,
,
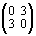 +
+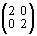 =
=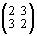 ;
;
–3 – 2 = – 5, 3 + 1 = 4, –3 + 2 = – 1.
Последняя операция подсказывает нам, что числу –1 может соответствовать бесконечное число матриц. Аналогично, любому другому числу — отрицательному или положительному — будут соответствовать бесконечные ряды матриц. Это означает расширение числового поля, сконструированного на матрицах. Можно сказать, что все матрицы последнего ряда проецируются на единственное число: –1; или, что указанный ряд имеет модуль: –1. Умножению чисел, например: 7 ´ (–3) = – 21, будет отвечать бесчисленное количество умножений на матрицах, которые, однако, будут давать всегда эквивалентные результаты, например:
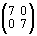 ´
´
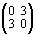 =
= 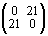 ,
,
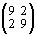 ´
´
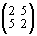 =
= 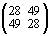 ,
,
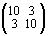 ´
´
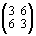 =
= 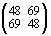 ;
;
здесь получается один и тот же результат: – 21 = 28 – 49 = 48 – 69.
Теперь возьмем две матрицы размером 3 ´ 3, представим их двумя различными способами и перемножим обычным образом. Пусть даны две числовые матрицы A и B, которые мы представим в виде A1, A2 и B1, B2, имеем:
A = 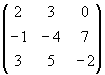 , A1 =
, A1 =  ,
A2 =
,
A2 =  , ...
, ...
B = 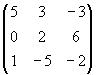 , B1 =
, B1 =  ,
B2 =
,
B2 =  , ...
, ...
Произведем обычное перемножение матриц A, B, A1, A2, B1, B2:
A ´ B = 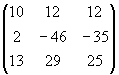 ,
A2 =
,
A2 = 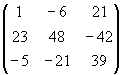 , B2 =
, B2 =
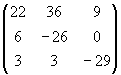 ,
,
A1 ´ B1 =  ,
A1 ´ B2 =
,
A1 ´ B2 = 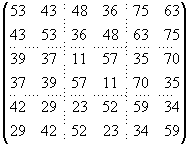 ,
,
A2 ´ B1 =  ,
A2 ´ B2 =
,
A2 ´ B2 = 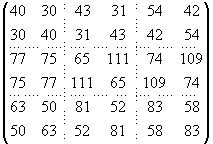 ,
,
Сравнение элементов матриц дает нам право заключить, что все результирующие матрицы эквивалентны друг другу:
A ´ B » A1 ´ B1 » A1 ´ B2 » A2 ´ B1 » A2 ´ B2 ,
поскольку первые элементы у них равны одному и тому же числу:
10 = 14 – 4 = 53 – 43 = 15 – 5 = 40 – 30.
Аналогичные равенства выполняются для остальных элементов.
Теперь возьмем две эквивалентные матрицы A1 и A2 и тоже найдем их всевозможные произведения:
A1 ´ A1 =
, A1 ´ A2 =
,
A2 ´ A1 =
, A2 ´ A2 =
.
И вновь мы обнаруживаем эквивалентность их относительно квадрата матрицы A:
A2 » A1 ´ A1 » A1 ´ A2 » A2 ´ A1 » A2 ´ A2 ,
так как первые элементы матриц равны:
1 = 18 – 17 = 57 – 56 = 8 – 7 = 33 – 32;
все прочие элементы также удовлетворяют соответствующим равенствам. Поиск матриц, эквивалентных квадрату B2, даст аналогичный результат.
Можно попытаться найти в общем виде формально-логическое доказательство фигурирующей у нас эквивалентности, однако конструктивист не станет этого делать, так как оно не прибавит ему новых знаний, а лишь затормозит его продвижение вперед. Что же касается достоверности свойств введенных им самим матриц, то он в них не сомневается; он уверен, что ни одна из числовых матриц его не подведет, так как они как раз и были сконструированы так, чтобы отделить так называемые отрицательные числа от положительных, подобно тому, как в комплексных числах отделены действительная и мнимая части. Если с какими-нибудь конкретными матрицами возникнут проблемы, конструктивист просто будет пытаться их разрешить своими конструктивными методами. Все проблемы формалиста традиционно лежат в плоскости логических доказательств, которые неизбежно имеют дело только с символами, в действительности же требуется исчислять конкретные объекты, скрывающиеся за этими символами.