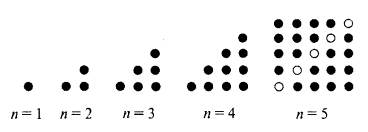Конструктивная математика

Акимов О.Е.

20. Шесть доказательств одного выражения

Сильно ошибаются те, кто думает, что с помощью формально-логического вывода можно добыть принципиально новые знания. Мы уже говорили, что логические доказательства нужны математикам скорее для убеждения коллег в своей правоте. В среде математиков существует негласное правило: приступай к поиску доказательства только после того, как убедился в истинности доказываемого предложения. Это здравый совет. Аксиомы, леммы и теоремы — все равно, что юридические нормы, регулирующие отношения людей в обществе: они должны быть завершенными, непротиворечивыми, лаконичными и общепризнанными, чтобы не вызывать путаницы. Если же вы хотите проникнуть в реальный мир математики и познать объективную красоту формул, лучше воспользоваться эффективными вычислительными процедурами.

Чтобы лучше усвоить эту важную мысль, докажем несколькими способами элементарное равенство:

1 + 2 + 3 + ... + n = n(n + 1)/2.         (1)

Доказательство 1 (по индукции).

Формула (1) верна, если она верна для n = 1, n = k, n = k + 1. Для первых двух значениях n имеем

1 = 1 · (1 + 1)/2,     1 + 2 + 3 + ... + k = k · (k + 1)/2.

К левой и правой частям равенства прибавим член ряда (k + 1):

1 + 2 + 3 + ... + k + (k + 1) = k · (k + 1)/2 + (k + 1).

Правую часть нетрудно представить в виде (k + 1)(k + 2)/2, что соответствует формуле (1) при третьем значении n. Теперь у нас появилась уверенность в том, что эта формула будет работать при любых целых значениях n. Однако мы остались в неведении относительно того, откуда взялась формула.

Легко устанавливается, что сумма нечетных чисел равна квадрату числа слагаемых:

1 + 3 + 5 + ... + (2n – 1) = n².    ;       (2)

Действительно, последовательно увеличивая длину суммируемого ряда, мы быстро улавливаем закономерность:

1² = 1²,  1 + 3 = 2²,  1 + 3 + 5 = 3²,  1 + 3 + 5 + 7 = 4², ...

Сравнительно просто находится формула для суммы кубов натурального ряда:

1³ + 2³ + 3³ + ... + n³ = [n(n + 1)/2]².    (3)

Она вытекает из следующих сумм:

1³ = 1², 1³ + 2³ = 3², 1³ + 2³ + 3³ = 6², 1³ + 2³ + 3³ + 4³ = 10², ...

Но попробуйте подобрать формулу для суммы квадратов натурального ряда —

1² = 1, 1² + 2² = 5, 1² + 2² + 3² = 14, 1² + 2² + 3² + 4² = 30, 

1² + 2² + 3² + 4² + 5²= 55, ...

Это сделать уже непросто. Поэтому ценны именно те методы, которые не только подтверждают, но и выводят формулу.

Доказательство 2 (для суммы арифметической прогрессии)

Операция сложения подчиняется коммутативному закону. Сложение членов ряда произведем парами, элементы которых равноудалены от концов ряда. Пусть число элементов в ряду будет сначала четным, т.е. n = 2k, тогда

1 + 2 + 3 + ... + (2k – 2) + (2k – 1) + 2k =

= [1 + 2k] + [2 + (2k – 1)] + [3 + (2k – 2)] + ... + [k + (2k – (k – 1))] = 

= [1 + 2k] + [1 + 2k] + [1 + 2k] + ... + [1 + 2k] =

= [1 + 2k]k = n(n + 1)/2.

Пусть число элементов в ряду нечетно, n = 2k + 1, тогда

1 + 2 + 3 + ... + k + (k + 1) + (k + 2) + ... + (2k – 1) + 2k + (2k + 1) =

= [1 + (2k + 1)] + [2 + 2k] + [3 + (2k – 1)] + ... + [k + (k + 2)] + (k + 1) =

= [2 + 2k] + [2 + 2k] + [2 + 2k] + ... + [2 + 2k] + (k + 1) =

= [2 + 2k]k + (k + 1) = (k + 1)(2k + 1);

при k = (n – 1)/2 получим n(n + 1)/2.

Подобное доказательство справедливо для всех рядов вида

a₁, a₁ + d, a₁ + 2d, ... , a₁ + (n – 1)d,

которые называются арифметическими прогрессиями. Разность (d) и первый член (a₁) арифметической прогрессии могут быть любыми действительными числами, но число элементов в ряду по-прежнему равно либо четному, либо нечетному целому. Поэтому суммы пары равноудаленных элементов, равные 2a₁ + (n – 1)d, нужно рассматривать для четного и нечетного числа n. В обоих случаях результат сводится к формуле:

= (a₁ + a_n) n/2.         (4)

Формула (4) переходит в (1) при подстановке a₁ = 1 и a_n = n.

Последнюю формулу легко понять, если понимается следующее:

(a₁ + a_n)/2 = (a₂ + a_{n – 1})/2 = (a₃ + a_{n – 2})/2 = ... = (a_n/2 + a_{n – n/2})/2

т.е. среднее арифметическое двух равноудаленных от концов ряда элементов всегда равно одному и тому же числу — центру арифметической прогрессии. Если число элементов прогрессии нечетно (n = 2k + 1), то центр арифметической прогрессии совпадает с центральным членом ряда (a_{k + 1}); если число элементов четно (n = 2k), то центр равен среднеарифметическому двух серединных элементов (a_k + a_{k + 1})/2. В частности, для нечетного n = 5 имеем

1 + 2 + 3 + 4 + 5 = (1 + 5)5/2 = 15;

центр арифметической прогрессии приходится на элемент 3:

(1 + 5)/2 = (2 + 4)/2 = 3.

Для четного n = 6 имеем 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6)6/2 = 21;

центр равен

(1 + 6)/2 = (2 + 5)/2 = (3 + 4)/2 = 3,5.

Таким образом, второе доказательство дало нам больше, чем мы рассчитывали: мы не только подтвердили и вывели формулу (1), но и нашли существенно более общую формулу (4). Так, если нам дана арифметическая прогрессия с параметрами: a₁ = – 2,54, d = 0,127, n = 57, то, воспользовавшись формулой (1), можно без труда подсчитать сумму (S) всех ее 57 элементов:

S = = (a₁ + a_n)n/2 = [2a₁ + (n – 1)d]n/2 =

= [2 · (–2,54) + 56 · 0,127] · 57/2 = 57,912.

Несколько иной взгляд на сумму S приходит к нам, если члены арифметической прогрессии расположить по следующей схеме:

						d	...
					d	d	...
				d	d	d	...
			d	d	d	d	...
		d	d	d	d	d	...
	a1	a1	a1	a1	a1	a1	...

Тогда S можно представить как сумму двух составляющих S₁ и S₂:  

S = S₁ + S₂ = 57,912; 

где     S₁ = n · a₁ = 57 · (– 2,54) = – 144,78 , 

S₂ = n · (n – 1) · d/2 = 57 · 56 · 0,127/2 = 202,692.

Здесь для подсчета S₂ используется формула (1).

Доказательство 3 (связанное с биноминальным разложением)

В биноминальное разложение

(x + 1)² = 1 + 2x + x²     или     (x + 1)² – x² = 1 + 2x

вместо x поочередно будем подставлять числа 1, 2, 3, ..., n. В результате получим следующую систему равенств:

2² – 1² = 1 + 2 · 1,     3² – 2² = 1 + 2 · 2,     

4² – 3² = 1 + 2 · 3,     ... ,     (n + 1)² – n² = 1 + 2 · n.

Произведем сложение правых и левых частей этих равенств, получим выражение:

(n + 1)² – 1 = n + 2 · (1 + 2 + 3 + ... + n).

После очевидных преобразований приходим к (1).

Данную методику вывода можно распространить на сумму квадратов, кубов и более высоких степеней чисел натурального ряда. В самом деле, возьмем кубический бином:

(x + 1)³ – x³ = 1 + 3x + 3x³ .

Поочередно присвоим x числа 1, 2, 3, ..., n, а затем, производя те же самые операции, что и в предыдущем случае, найдем ранее ненайденную формулу для суммы квадратов натурального ряда:

(n + 1)³ – 1 = n + 3 · n · (n + 1)/2 + 3 · (1² + 2² + ... + n²);

1² + 2² + ... + n² = n³/3 + n²/2 + n/6 = 

= n · (n + 1) · (2n + 1)/6.         (5)

Используя тетрабином (x + 1)⁴, находим формулу (3).

При доказательстве формулы (1) не обязательно ограничиваться только символьной манипуляцией. Ниже рассматриваются еще три способа доказательства, где существенную роль играют операции с графическими объектами.

Доказательство 4 (связанное с представлением целых чисел геометрическими точками).

Рис. 19

Поставим каждому целому числу натурального ряда соответствующую совокупность точек на плоскости. Тогда сумма числовых рядов предстанет перед нашим взором в виде некоторого множества точек, образующих треугольник. На рис. 19 для случая n = 5 показано, каким образом можно было бы подсчитать число точек в треугольнике. Для этого необходимо произвести следующие алгоритмические операции:

1) подсчитать число точек в квадрате — n · n;

2) вычесть из полученного числа точки, стоящие в диагонали — 

n · n – n = n · (n – 1);

3) результат разделить пополам — n · (n – 1)/2;

4) к последнему числу прибавить ранее вычтенные диагональные точки — 

n · (n – 1)/2 + n = n · (n + 1)/2.

Однако с помощью точек несколько сложнее вывести следующую формулу для сумм, т.е. формулу для суммы сумм:

1 + 3 + 6 + 10 + ... + n · (n + 1)/2 = 

= n · (n + 1) · (n + 2)/6.         (6)

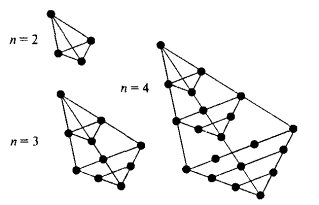
Подставляя в формулу (6) n = 1, 2, 3, 4, ..., будем получать числа — 1, 4, 10, 20, ..., которые можно проиллюстрировать точками в пространстве, а именно, пирамидами (рис. 20).

Рис. 20

Доказательство 5 (связанное с вычислением площади)

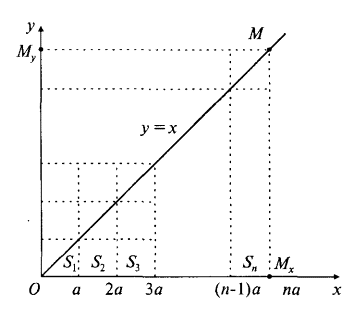
На рис. 21 приведены координатные оси и вычерчена прямая y = x. На прямой возьмем точку M и от нее на обе оси проведем перпендикуляры MM_x и MM_y. Отрезки 0M_x и 0M_y поделим на n частей, при этом длину каждой части примем за a, так что 0M_x = 0M_y = na.

Рис. 21

Подсчет площади S треугольника 0MM_x можно произвести двумя способами:

S = (0M_x)²/2 = n²a²/2     и     S = S₁ + S₂ + S₃ + ... + S_n.

Непосредственно из рис. 21 легко установить, как подсчитать площадь прямоугольной трапеции S_i :

S₁ = a² – a²/2,         S₂ = 2a² – a²/2, 

S₃ = 3a² – a²/2, ... , S_n = na² – a²/2.

Отсюда вытекает равенство:

S = a²(1 + 2 + 3 + ... + n) – na²/2 = n²a²/2.

Наконец, избавившись от a², находим формулу (1):

1 + 2 + 3 + ... + n = n²/2 + n/2 = n · (n + 1)/2.

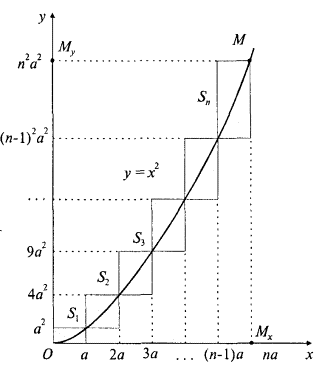
Рис. 22

Чтобы доказать формулу (5), необходимо изложенную только что методику распространить на объемы [35, с. 206]. На рис. 22 показаны несколько слоев кубиков (в общем случае n слоев), образующих пирамиду OABCD. Число кубиков по слоям сверху вниз равно: 1², 2², 3², ... n². Пусть объем каждого кубика равен a³ = 1. Тогда объем ступенчатой пирамиды, составленной из этих кубиков, равен сумме квадратов: 1² + 2² + 3² + ... + n². Если из полного объема большой пирамиды OABCD, равного (1 + n)³/3, вычесть все объемы маленьких пирамид типа EQPDK, в сумме дающих величину (1 + n)/3, и объемы всех призм типа AFHEQP и KQPBLM, в сумме дающих величину n(1 + n)/2, то получим следующее равенство:

1² + 2² + 3² + ... + n² = 

= (1 + n)³/3 – (1 + n)/3 – n(1 + n)/2 =

= n(1 + n)(1 + 2n)/6.

Как и в предыдущем случае, дальнейшее распространение подобной методики на сумму кубов невозможно, так как мы не умеем вычерчивать рисунки в четырехмерном пространстве.

Рис. 23

С помощью рис. 23 удается вывести формулу (2). Действительно, площадь прямоугольников S_i равна:

S₁ = a³,     S₃ = 3a³,     S₃ = 5a³,   ... ,   S_n = (2n – 1)a³.

Если выделенные сплошной линией прямоугольники составить один под другим, получится крайняя правая вертикальная полоса, площадь которой равна:

= a³ + 3a³ + 5a³ + ... + (2n – 1)a³ = n²a³.

Избавившись от a³, получаем выражение (2).

Доказательство 6 (связанное с представлением о полном графе)

Напомним, графом называется графический объект, состоящий из точек (вершин) и линий (ребер). Каждое ребро графа соединяет две точки (говорят: ребро ij инцидентно вершинам i и j). Но любая вершина графа может быть инцидентна нескольким ребрам. В связи с этим вводят понятие о валентности или степени связанности данной вершины с другими вершинами. Понятно, что на каждое ребро приходится по две валентности. Поэтому число ребер равно половине суммы степеней всех вершин:

         (7)

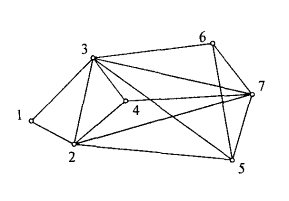
Формула (7) вытекает непосредственно из геометрического образа графа и только что введенных понятий. Проверяем, произвольно вычерченный граф (рис. 24) подчиняется этому соотношению:

14 = (2 + 5 + 6 + 3 + 4 + 3 + 5)/2.

Рис. 24

Конструктивисту не требуется более "строгое" обоснование формулы (7). 

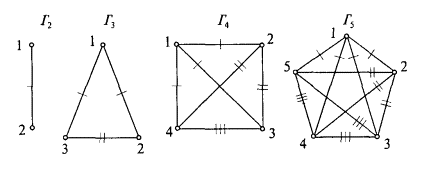
Напомним также, что граф называется полным, если каждая его вершина связана ребрами со всеми остальными вершинами. На рис. 25 представлены первые четыре полных графа Г_n. Для полных графов формулу (7) можно упростить, заменив сумму произведением двух величин: числа вершин (n) и степени одной из вершин (d = n – 1):

m = nd/2 = n(n – 1)/2.

Рис. 25

Так, для последнего графа Г₅, изображенного на рис. 25, число ребер равно 10 = 5 · 4/2; для следующего графа Г₆ будем иметь 15 = 6 · 5/2 и т.д.

Переходя от вершины к вершине и последовательно вычеркивая ребро за ребром, как показано на рис. 25, мы можем подсчитать число m иначе, а именно, как сумму чисел от 1 до n – 1. Например, для Г₅ получим 10 = 1 + 2 + 3 + 4, для Г₆ — 15 = 1 + 2 + 3 + 4 + 5 и т.д. Отсюда возникает система равенств:

 5 · 4/2 = 1 + 2 + 3 + 4,     6 · 5/2 = 1 + 2 + 3 + 4 + 5     и т.д., 

которая при обобщении порождает формулу (1), записанную не для n слагаемых, а для n – 1, что не меняет сути:

1 + 2 + 3 + ... + (n – 1) = n(n – 1)/2.

Итак, мы рассмотрели шесть различных способов доказательства справедливости одной и той же достаточно элементарной формулы (1) и при это производили небольшие демарши в сторону других формул (2) – (6), аналогичного строения. Какие же выводы в связи с этим можно было бы сделать?

Во-первых, нет никаких оснований считать какой-либо вывод более строгим, более убедительным или более исчерпывающим. В математике, как и в юриспруденции, ни одно из доказательств не имеет преимущественного значения. Они все имеют равное право на существование: вывод формулы (1) с помощью графических образов (точек, площадей или ребер графа) ничем не хуже вывода этой формулы на основе чисто символьных процедур, на основе представлений об арифметической прогрессии или бинома.

Однако, и это, во-вторых, графические способы вывода не имеют продолжения. Они ограничиваются доказательством данной конкретной формулы. Их методики не экстраполируются на многомерные случаи. Графические образы позволяют «видеть» элементарные формулы (1) и (2), но они не дают «увидеть» чуть более сложные формулы — (5) и (6). Тем не менее, особо подчеркнем, не нужно пренебрегать пространственными объектами, коль скоро их удается привлечь к анализу той или иной математической ситуации, поскольку рисунки сообщают абстрактным знаниям ту степень репрезентативности, которая как нельзя лучше способствует их усвоению.

В юриспруденции в качестве аргументов могут выступать показания свидетелей и вещественные улики. В математике графические образы можно отнести по юридической терминологии к вещественным, т.е. к аргументам прямого действия.

Основная же наша мысль состоит в третьем выводе, который вытекает из представленных здесь доказательств формулы (1). Задумаемся, а почему, собственно, символьные доказательства (второе и третье) оказались столь эффективны? Вышло так, что аналитическая методика обоснования формулы (1) оказалось значительно ценней самой формулы, поскольку она дала ключ к открытию новых формул. Не потому ли, что ряды арифметических прогрессий и ряды от биномов различной степени сами задают определенного рода регулярные процедуры, подчиняющиеся простой алгоритмизации.

Отсюда напрашивается еще более эффективная методика продуцирования новых формул, при которой числовые ряды (если речь идет о них) возникают не от случая к случаю, а путем осмысленного строительства, направленного конструирования. Такой конструктивизм приведет нас к методу исчисления рядов, когда истинность формулы устанавливается ее единственным атрибутом — местом в бесконечном ряду подобных формул. Это избавляет нас от трудоемкой процедуры ее специального обоснования логическими или графическими методами.