Конструктивная математика

Акимов О.Е.

24. Уравнение Шредингера

Понятие о стационарной атомной орбите электрона возникает из решения уравнения Шредингера. Что это за уравнение и как его получить? 

Его можно вывести из выражения для обобщенной плоской волны:

,

где ћ = h/2π — постоянная Планка, p — импульс и E — энергия. Если волновую функцию ψ один раз продифференцировать по времени и дважды по координатам:

, ,

а затем эти выражения приравнять по Eψ, помня, что E = p²/2m, то в результате и получим уравнение Шредингера, которое удобно переписать через оператор Ñ:

,

.

Среди всех решений данного уравнения имеются решения, зависящие только от времени:

.

Если это решение подставить в уравнение Шредингера, то оно и будет давать для электронов стационарные орбиты, зависящие только от переменной r :

.

В центрально-симметричном кулоновском поле с потенциалом V = –Ze²/r уравнение Шредингера обычно представляют очень коротко через оператор Гамильтона H:

Hψ =Eψ,    так как    ,

то .

Симметрия поля диктует соответствующую систему координат, а именно, сферическую:

x = r sin θ cos φ,   y = r sin θ sin φ,    z = r cos θ,

где r — радиус-вектор полярных координат, θ — полярный угол, φ — азимут.

В сферических координатах уравнение Шредингера запишется в виде:

.

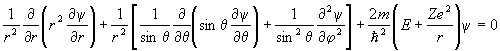Это уравнение с разделяющимися переменными по радиальной составляющей R и угловой Y имеет решение в форме произведения этих составляющих, т.е.

.

В этом виде волновая функция зависит от трех параметров:
n — главное квантовое число;
l = {0, 1, 2, …, n – 1} — орбитальное квантовое число;
m = {–l , –l + 1, –l + 2, … , 0, 1, 2, …, l – 2, l – 1, l } — магнитное квантовое число.

Радиальная часть волновой функции зависит от присоединенных полиномов Лагерра, которые имеют следующий аналитический вид для n = 1, 2, 3:

,

,

,

,

,

.

Примерный ход зависимости R от r показан на рис. 27а. Угловая часть волновой функции зависит от присоединенных полиномов Лежандра, которые имеют следующий аналитический вид для l = 0, 1, 2, 3:

,

,

,

,

,

,

,

,

,

.

.

Рис. 27а

.

Рис. 27б

.

Рис. 27в

Зависимости Y от θ и φ показаны на рис. 27б. Угловая составляющая определяет симметрию электронного уровня, а значит, и пространственную группу преобразований, которая оставляет электрон на этом уровне без изменений. Решениями уравнения являются не только сами значения, но и их линейная комбинация, что позволяет избавиться от мнимых величин. Например, комбинация из и имеет симметрию sin θ cos φ и т.д.

В табл. 23 приведены симметризованные функции для s, p и d орбиталей электронов.

Таблица 23

Орбиты	Симметрия
s	1
px	sin θ cos φ
py	sin θ sin φ
pz	cos θ
dxy	sin2 θ sin 2φ
dxz	sin 2θ cos φ
dyz	sin 2θ sin φ
dx2 – y2	sin2 θ cos 2φ
dz2	3cos2 θ – 1

Если волновые функции ψ_nlm определяют собственные векторы, то собственными значениями выступают энергии электронов, зависящие только от главного квантового числа по известной из модели Бора формуле:

E_n = .

Частота излучаемой или поглощаемой электромагнитной волны определяется тоже по известной формуле Бальмера:

f_mn = (E_n – E_m)/h = =

= где m < n.

Диаграмма уровней энергии электронов в атоме водорода показана на рис. 27в.

Волновая функция электрона, находящегося в стационарном состоянии, т.е. когда энергия системы не зависит от времени, записывается следующим образом:

ψ(k, r) = exp [i (k · r)] = exp [i (k_xx + k_yy + k_zz)],

где k — волновой вектор, природу которого мы сейчас выясним. С этой целью найдем первую и вторую производную волновой функции по координате x:

, .

Точно так же продифференцируем ψ по y и z. Помня, что k² = k²_x + k²_y + k²_z , подставим вторые производные в уравнение Шредингера

,

,

.

В последнем уравнении сократим ψ и выразим энергию E, получим

= ε( k²_x + k²_y + k²_z ).

Перед нами квадратичный закон дисперсии E(k), играющий центральную роль в теории энергетических уровней электронов в кристаллах полупроводников и металлов. Слово дисперсия с латинского переводится как рассеяние. Следовательно, закон дисперсии E(k) следует понимать как закон рассеяния периодического процесса. Так, звуковые волны при прохождении через среду изменяют свою форму, что называется акустической дисперсией. На дисперсию света влияет коэффициент преломления среды, который будет различным для различных длин волн. В частности, белый свет рассеивается на свои составные части, т.е. мы наблюдаем его спектральное разложение. Явление рассеяния наблюдается также при дифракции и интерференции волн любой природы. Коль скоро волновые функции электронов представляются плоскими или сферическими волнами, то и их дисперсия, т.е. рассеяние, на узлах кристаллической решетки есть вполне естественный физический процесс.

С точки зрения аналитической геометрии, квадратичный закон дисперсии представляет собой уравнение сферы в k-пространстве, которое пока для нас остается тайной. Значит, изоэнергетические поверхности или поверхности постоянной энергии будут представлять собой сферы. Прежде чем уяснить, что такое пространство k, необходимо понять, через что выражается число k. Для этого выразим кинетическую энергию электрона посредством импульса:

.

Приравняв оба выражения для энергии, мы понимаем смысл волнового числа k:

p² = ћ²k²,    p = ћk,    k = p/ћ = 2πp/h.

Если вспомнить о длине волны де Бройля: λ = h/mv = h/p, то окончательно для волнового числа получим выражение: k = 2π/λ. Таким образом, волновое число k — это число длин волн, укладывающихся на длине окружности, выраженной в радианах, т.е. на длине 2π.

Данное представление о длине волны ассоциируется с представлением о круговой частоте ω = 2π/Т, для которой T есть период колебания какой-либо физической величины во времени t. По аналогии, волновое число k отражает пространственную круговую частоту, т.е. колебание какой-либо физической величины, распределенной в пространстве r. Такая периодичность возникает в твердых веществах, имеющих кристаллическую решетку с периодом a.

Поэтому для кристаллических веществ волновое число приобретает новое содержание: во-первых, его записывают как k = 2π/a; во-вторых, волновое число становится вектором, поскольку узлы решетки существуют в пространстве трех измерений (далее под k мы будем всегда понимать именно вектор, поэтому не станем его каким-либо образом выделять). Так возникает понятие о k-пространстве, которое является обратным по отношению к r-пространству.

Подобно тому, как периодические функции во времени f(t) = f(t + T) часто выражают через преобразование Фурье, получая спектральную характеристику F(ω), точно так же периодические функции в пространстве f(r) = f(r + R) удобно представлять через преобразование Фурье в k-пространстве. Таким образом, закон дисперсии E(k) — это спектр энергии.

Если бы речь шла об энергетическом спектре в виде E(ω), то смысл данной зависимости состоял бы в следующем. Числовые значения E(ω₁), E(ω₂), …, E(ω_n) говорили бы о значениях энергии, приходящихся на частоты и ω₁, ω₂, …, ω_n какого либо периодического процесса. Например, частота рентгеновского излучения способна переносить большую энергию, а частота видимого света — малую. 

По аналогии дискретные значения энергии в k-пространстве E(k₁), E(k₂), …, E(k_n) говорят о распределении энергии в обратном пространстве кристалла по конкретным значениям волнового вектора k₁, k₂, …, k_n. В частности, энергия электронов может зависеть от направления волнового вектора в решетке при равном его модуле, что вызвано анизотропией кристалла. Квадратичный закон дисперсии, дающий сферическую поверхности в k-пространстве, говорит об отсутствии анизотропии; этот закон и был получен для свободных электронов, находящихся вне кристалла.

Поскольку кристаллические решетки могут быть различными, то в законе дисперсии E(k) будет присутствовать так называемый структурный фактор S(K), определяемый конкретной конфигурацией решетки. Потенциал кулоновского поля атомов, образующих решетку, определяет форм-фактор v(K), который тоже будет принимать различные значения для различных атомов, входящих в данную решетку. Таким образом, закон дисперсии E(k) выражается как некая комбинация структурного фактора S(K) и форм-фактора v(K). 

Структурный фактор часто задается той или иной матрицей, в которой имеются нулевые и ненулевые матричные элементы. В этом случае форм-фактор выступает в виде числовых значений матричных элементов. Вид матрицы для сходных материалов, например кремния и германия, будет одинаковым, но величины матричных элементов для них – различны. Матричные элементы зависят также от координат k-пространства, как функция от аргумента. 

Полный закон дисперсии E(k) определяется всеми собственными значениями матрицы, описывающей данную электронную систему, для каждой точки k-пространства. На практике часто бывает достаточно определить закон дисперсии в определенных направлениях k-пространства или даже в нескольких характерных точках, причем берут не все, а только несколько нижних собственных значений (верхние уровни энергии, лежащие в зоне проводимости высоко над запрещенной зоной, чаще всего не интересуют практиков).

Далее нам понадобится еще одно важное понятие, непосредственно вытекающее из закона дисперсии E(k), который для реальных материалов отличается от сферической формы. Однако введенное ниже понятие остается в силе и тогда, когда закон дисперсии не носит квадратичную зависимость от волнового вектора. Итак, найдем первую, затем вторую производную энергии по волновому вектору k, когда закон дисперсии задан квадратичной формулой, и выразим массу:

= , ,

, ,

Вторая производная характеризует кривизну поверхности закона дисперсии E(k). У нас получилось, что масса электрона обратно пропорциональна кривизне закона дисперсии. Чем больше кривизна, тем меньше масса и, наоборот. Так как уравнение E(k) представляло сейчас сферу, поверхность которой имеет постоянную кривизну, то куда бы ни летел электрон, он будет иметь постоянную массу, равную массе свободного электрона. Но в кристалле функция E(k) не квадратична, изоэнергетические поверхности отличаются от сферических и, следовательно, масса электрона зависит от направления в k-пространстве и величины второй производной от энергии. Скалярная величина массы превращается в тензорную величину, которая называется эффективной массой: 

если d²E/dk² > 0, то m > 0; если d²E/dk² < 0, то m < 0. 

Отрицательной массой обладают дырки, положительной — электроны. При смене знака вторая производная закона дисперсии должна быть равна нулю: d²E/dk² = 0, что соответствует бесконечно большому значению массы электрона или дырки. Никакая сила не способна перенести частицы с массой m = ± ∞; отсюда следует, что понятие эффективной массы имеет физическое значение вблизи нижнего края зоны проводимости для электронов и вблизи верхнего края валентной зоны для дырок.