Конструктивная математика
Акимов О.Е.
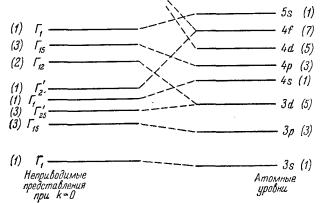
28. Модель слабой связи
Существует две принципиально различные расчетные модели: модель слабой связи и модель сильной связи. К модели сильной связи относится та, которой мы до сих пор пользовались, когда составляли ЛКАО-гамильтониан. В этой модели все электроны оказываются связанными с ядрами своих атомов, и только сближение этих атомов внутри кристалла приводит к перекрыванию волновых функций электронов, что влечет за собой перестройку орбиталей. Мы рассказывали, что в рамках этой модели при сближении атома a с атомом b возникают две линейные комбинации из двух атомных орбиталей χa и χb, а именно: симметричная χa + χb (нижний энергетический уровень) и антисимметричная χa – χb (верхний энергетический уровень). Чем ближе атомы в кристалле, тем интенсивнее взаимодействие между электронами, а значит, тем больше значения интегралов перекрытия атомных орбиталей, которые выступают в качестве матричных элементов в матрице ЛКАО-гамильтониана. Было сказано, что модель сильной связи удовлетворительно описывает закон дисперсии электронов ЗВ, т.е. связанные состояния, и неудовлетворительно — ЗП, т.е. свободные состояния.
В модели слабой связи электроны перемещаются внутри кристалла почти свободно. Отсюда другое название для этого приближения: модель почти свободных электронов. В нулевом приближении потенциал узлов решетки принимается за ноль, электрон абсолютно свободно перемещается внутри решетки; его движение описывается квадратичным законом дисперсии. При потенциале, отличном от нуля, электрон теряет часть свободы перемещения, закон дисперсии становится отличным от квадратичного, но зависимость движения электрона от потенциала решетки выражена все же намного слабее, чем в модели сильной связи.
Такова общая картина, которую можно немного конкретизировать, если перейти на язык плоских волн и условия их отражения на плоскостях Брэгга. Условие Брэгга формулируется следующим образом(k + K)2 = k2, k = ±½K = ±nπ/a.
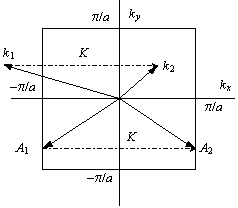
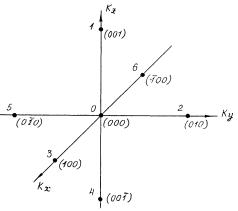
Это условие, собственно, и определяет границы ЗБ, где происходят отражения. Действие условия можно проиллюстрировать рис. 40, где изображена ЗБ от плоской ПК решетки. Вектор обратной решетки K преобразует вектор k1, выходящий за пределы первой ЗБ, в вектор k2, целиком находящийся внутри первой ЗБ. Точка A1, имеющая координату по оси абсцисс, равную –π/a, с помощью вектора K отражается на противоположном ребре в точку A2 с координатой π/a.
Рис. 40
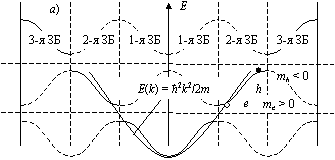
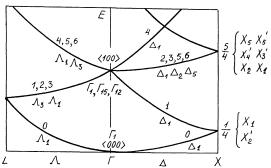
Квадратичный закон дисперсии E(k) (парабола) при отличном от нуля потенциале узлов решетки (V(K) ≠ 0) распадается на совокупность кривых S-образной формы разрешенного энергетического диапазона, разделенных зонами запрещенной энергии (рис. 41а, сплошные жирные линии). Однако всю эту кусочноквадратичную форму, распростертую по 1-й, 2-й, 3-й и т.д. ЗБ, можно спроецировать в пространство единственной 1-й ЗБ, как это показано на рис. 41б. Условие отражения Брэгга позволяет представить закон дисперсии в периодической схеме зон, где каждая ЗБ повторяет 1-ю ЗБ (рис. 41а, пунктирные кривые). За счет появления ЗЗ энергии (затемненная область) на квадратичной зависимости E(k) появляются участки с положительной и отрицательной кривизной, что отвечает, соответственно, положительной эффективной массе электронов μe (светлые кружочки) и отрицательной эффективной массе дырок μh (темные кружочки).
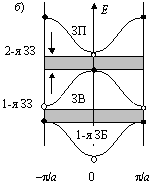
Рис. 41
Расположение их на расширенной зонной схеме предопределяет расположение их и на приведенной схеме. Более точные расчеты показывают, что 1-я ЗЗ практически отсутствует, так как электроны находятся на связанных энергетических уровнях, принадлежащих ядрам атомов. Диапазон энергий, расположенный ниже 2-ой ЗЗ, образует ЗВ, а выше 2-ой ЗЗ — ЗП; 3-ю или 4-ю ЗЗ, так же, как и 2-ю или 3-ю ЗП, тоже обычно не различают, так как модель сильной связи подсказывает, что электроны и дырки могут быть либо связанными, либо свободными; выше 2-ой ЗЗ они свободны и неразличимы, с точки зрения электропроводности материала. Однако многочисленные переходы электронов и дырок с одного уровня на другой уровень ЗП регистрируются оптическими приборами, поэтому их симметрию и расположение в обратном пространстве кристалла установить можно. Качественная модель слабой связи, изображенная на рис. 41, по уровню сложности соответствует примерно качественной модели сильной связи, изображенной на рис. 30. Далее перейдем к количественным расчетам, для чего составим матрицу гамильтониана в приближении почти свободных электронов. Но прежде, чем к этому приступить, сделаем следующее примечание.
Рис. 42
Несмотря на то, что язык двух физических моделей сильной и слабой связи, как видим, и терминологически и по содержанию различается заметно, описание симметрии энергетических уровней, с точки зрения теории групп, в них одинаковое. В модели сильной связи оперируют понятиями атомных и молекулярных орбиталей; в модели слабой связи свободно парящие электроны описываются Г-состояниями кристаллической решетки (рис. 42). В модели сильной связи считается, что симметрия электронных уровней в кристалле определяется симметрией электронных уровней отдельного атома, при этом умалчивается, чем, собственно, определяется симметрия уровней отдельно взятого атома. В модели слабой связи, наоборот, говорится, что симметрия электронных уровней вблизи отдельных узлов кристаллической решетки определяется симметрией всей решетки, при этом умалчивается, почему, собственно, кристаллическая решетка приобрела именно такую, а не иную симметрию. В обоих подходах отсутствует ответ об источнике симметрии для свободного атома (в модели сильной связи) и для кристаллической решетки (в модели слабой связи). Очевидно, что источником симметрии в обоих случаях является вакуум, который удобно смоделировать в виде абсолютно твердой кристаллической среды, внутри которой возникают энергетические возбуждения либо в форме свободных атомов водорода, гелия и т.д., либо связанных кристаллических решеток германия, кремния и т.д. Симметрия электронных состояний «свободного» атома или кристаллической решетки продиктована кубической упаковкой шаров вакуумной среды. В природе уже найдены аналогичные физические системы в виде экситонного газа или электронно-дырочной жидкости, которые являются сверхвеществом внутри обычного вещества. Пара электрон — дырка описывается с помощью обычного уравнения Шредингера на языке водородоподобных состояний; различие касается только количественной стороны: величина боровского радиус, энергия связи и прочие характеристики для экситона будут на порядок или два различаться.
Для электронно-дырочных пар кристаллическая решетка выступает в роли эффективного вакуума, т.е. нейтрального фона, который находится совершенно в другом энергетическом диапазоне. Модель такой кристаллической вакуумной среды может объяснить множество ранее нерешенных физических проблем. Например, чем вызван поперечный характер электромагнитного излучения, почему отсутствует эфирный ветер, почему масса зависит от скорости движения, почему мир трехмерен, откуда атом водорода далекой звезды «знает», какую частоту электромагнитных волн ему излучать и т.п. Именно существование мировой среды делает нашу вселенную гармоничным и связанным организмом, вакуум же делает ее для нас непонятной. Но не станем далее вдаваться в выяснение первопричин симметричного устройства мироздания, а перейдем к рассмотрению конкретных задач, которые удается решить в рамках модели слабой связи.
Закон дисперсии E(k), как было сказано выше, задает возможные энергетические уровни, которые могут занимать электроны и дырки, находясь в обратном пространстве кристалла. В отсутствии всякого потенциала (V = 0), говорят, для «пустой решетки», решением уравнения Шредингера является простая квадратичная зависимость в виде:
E(k) = ћ2(k – K)2/2m,
где
— волновой вектор 1-й ЗБ;
— вектор, пробегающий все узлы обратной решетки.
Нам удобно измерять энергию в единицах ε:
ε =
.
Тогда закон дисперсии E(k) запишется как
ε(k) = (kx – n1)2 + (ky – n2)2 + (kz – n3)2.
Волновая функция, соответствующая квадратичному решению, равна:
ψ = exp[ir(k + K)] =
= exp (i2π/a)[(kx – n1)x + (ky – n2)y + (kz – n3)z].
В центре ЗБ (симметричная точка Г), на ее квадратной грани (точка Х) и на линии, проведенной между этими точками (симметричное направление Δ), значения энергии будут следующими (точка X для ПК решетки имеет kx = ½, для ГЦК kx = 1):
=
+
+
,
=
+
+
,
=
+
+
.
Для вектора
указанные энергии принимают значения:
= 0,
=
, εХ = ¼.
Волновая функция для
= 0 равна ψГ = 1 и, следовательно, принадлежит неприводимому представлению Г1; для направления D она принимает значения ψΔ = exp (i2πkx x/a), а точка Х двукратно вырождена, так что ей отвечают две волновые функции
ψ(Х) = exp (i2π x/a), ψ*(Х) = exp (–i2π x/a),
Из них можно составить две линейные комбинации, обладающие симметричными и антисимметричными свойствами, характерными для представлений Х1 и Х'4:
ψ(Х1) = ψ(Х) + ψ*(Х) =
= exp (i2πx/a) + exp (–i2πx/a) = 2cos (2πx/a),
ψ(Х'4) = ψ(Х) – ψ*(Х) =
= exp (i2πx/a) – exp (–i2πx/a) = 2i sin (2πx/a).
Сейчас для вектора {100} = {(100), (010), (001), (–100), (0–10), (00–1)} мы попытаемся понять, почему закон дисперсии в симметричном направлении распадается на шесть состояний именно так, а не иначе. Для этого рассмотрим движение электрона в ПК решетки вдоль оси kz. Электрон, двигаясь от точки 0 (000) к точке 1 (001) (рис. 43а), прочерчивает одно энергетическое состояние, которое обозначим через 0 (рис. 43б). Шесть состояний от шести узлов ПК решетки находятся на одинаковом расстоянии, равном единице, причем узлы 2, 3, 5 и 6 находятся в одинаковом положении. Поэтому на энергетической диаграмме появится четырехкратно вырожденное состояние. Еще два одномерных состояния образованы узлами 1 и 4. Так как при движении к узлу 1 расстояние уменьшается, а относительно узла 4 увеличивается, то и энергетические уровни относительно точки (001) получаются: одно нисходящее — 1, а другое восходящее — 4. Нисходящее состояние 1, соединясь с состоянием 0, идущим от вектора обратной решетки с координатами (000), дает двукратное вырождение с состояниями Х1 и Х'2. Если электрон движется по пространственной диагонали куба (Λ-направление), разрешенными для точки Г{100} будут только две трехкратно вырожденные траектории (1, 2, 3) и (4, 5, 6) и одно (0) однократно вырожденное для точки Г(000).
а)
б)
Рис. 43
Шесть векторов {100} дадут шесть волновых функций:
ψ1 = exp (i2π x/a), ψ2 = exp (i2π y/a),
ψ3 = exp (i2π z/a), ψ4 = exp (–i2π x/a),
ψ5 = exp (–i2π y/a), ψ6 = exp (–i2π z/a).Из этих шести волновых функций можно скомбинировать шесть симметризованных функций, которые определят три неприводимых представления: однократно вырожденное состояние Г1, двукратно вырожденное Г12 и трехкратно вырожденное Г15 по следующим формулам:
ψ(Г1) = ψ1 + ψ2 + ψ3 + ψ4 + ψ5 + ψ6 =
= cos (2πx/a) + cos (2πy/a) + cos (2πz/a);
ψ(Г12)1 = – ψ1 – ψ2 + 2ψ3 – ψ4 – ψ5 + 2ψ6 =
= 2cos (2πz/a) – cos (2πx/a) – cos 2πy/a);
ψ(Г12)2 = ψ1 – ψ2 + ψ4 – ψ5 = cos (2πx/a) – cos (2πy/a),
ψ(Г15)1 = ψ1 – ψ4 = sin (2πx/a),
ψ(Г15)2 = ψ2 – ψ5 = sin (2πy/a),
ψ(Г15)3 = ψ3 – ψ6 = sin (2πz/a).Вектор обратной решетки {111} распадается на восемь состояний, которые определят восемь волновых функций:
exp [i2π (x + y + z)/a], exp [i2π (x + y – z)/a],
exp [i2π (–x + y + z)/a], exp [i2π (x – y + z)/a],
exp [i2π (–x – y – z)/a], exp [i2π (–x – y + z)/a],
exp [i2π (x – y – z)/a], exp [i2π (–x + y – z)/a].Из этих функций можно построить восемь симметризованных функций, которые удовлетворяют четырем неприводимым представлениям: Г1, Г'2, Г'25 и Г15 по следующим формулам:
ψ(Г1) = cos (2πx/a) cos (2πy/a) cos (2πz/a),
ψ(Г'2) = sin (2πx/a) sin (2πy/a) sin (2πz/a),
ψ(Г'25)1 = cos (2πx/a) sin (2πy/a) sin (2πz/a),
ψ(Г15)1 = sin (2πx/a) cos (2πy/a) cos (2πz/a),
ψ(Г'25)2 = sin (2πx/a) cos (2πy/a) sin (2πz/a),
ψ(Г15)2 = cos (2πx/a) sin (2πy/a) cos (2πz/a),
ψ(Г'25)3 = sin (2πx/a) sin (2πy/a) cos (2πz/a),
ψ(Г15)3 = cos (2πx/a) cos (2πy/a) sin (2πz/a).Итак, мы показали принцип нахождения собственных значений энергии и волновых функций для ПК решетки в отсутствии заряда ядер, т.е. когда энергия целиком определяется волновым вектором k. Для ГЦК решетки, которую имеют большинство полупроводников, кристаллизующихся по типу алмаза или цинковой обманки, законы дисперсии ε(k) ищутся аналогичным образом. Энергетические уровни в отсутствии потенциала (V = 0) по трем симметричным направлениям Δ, Λ, Σ показаны на рис. 44а. На энергетических уровнях числами 1, 2, 3, 4, 6, 8, 12, 24 показаны степени вырождения энергетических состояний, соответствующие либо симметричным точкам, либо симметричным направлениям ЗБ (рис. 38). На рис. 44б приведена реальная зонная структура германия для тех же трех направлений при V ≠ 0.
а)
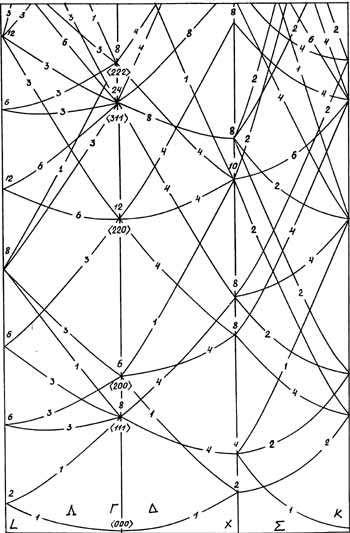
б)
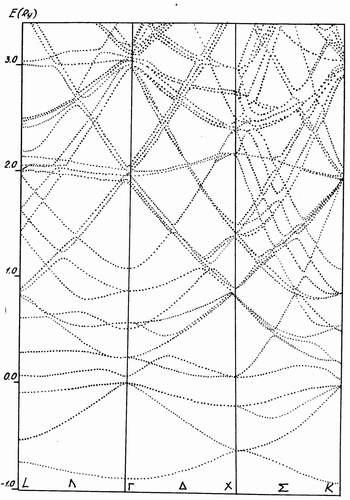
Рис. 44
Расскажем чуть более подробно, как производится расчет энергетических уровней для реального полупроводника при наличии кристаллического потенциала. С это целью введем компактные обозначения Дирака. Плоскую волну и ее сопряжение он обозначил как
ψ = exp[ir(k + K)] = | k + K > и
ψ* = exp[–ir(k + K)] = < k + K |.
Тогда уравнение Шредингера запишется в следующем виде:
(T + V ) | k > = E | k >,
где T и V — кинетическая и потенциальная составляющие гамильтониана H. Блоховская функция, разложенная в ряд Фурье, теперь выглядит так:| k > = ΣK a(K) | k + K >,
где a(K) — коэффициенты Фурье. Подстановка разложенной функции | k > в уравнение Шредингера даст уравнение:
ΣK a(K) (T + V – E) | k + K > = 0.
Умножим последнее уравнение на сопряженную плоскую волну с фиксированным вектором обратной решетки K', получим
ΣK {(T – E) δKK' + < k + K' | V | k + K >}a(K) = 0,
где < k + K' | V | k + K > — матричный элемент потенциала. Система уравнений имеет решение, если ее детерминант приравнять нулю:det{[ ћ2(k – K)2/2m – E] δKK' + < k + K' | V | k + K >} = 0.
Матричный элемент потенциала зависит только от разности векторов K' – K, тогда
< k + K' | V | k + K > = V(K' – K) = Σi Si (K' – K) vi (K' – K),
где Si (K' – K) — структурный фактор, vi (K' – K) — форм-фактор потенциала i-ого узла решетки.
Таким образом, матричный элемент потенциала есть произведение структурного фактора на форм-фактор. Следовательно, матрица гамильтониана размером 15 × 15, в которой учтены одно состояние от вектора {000}, восемь состояний от вектора {111} и шесть состояний от вектора {200}, будет представлять табл. 29. Для полупроводников IV группы она будет симметричной, следовательно, достаточно привести ее верхнюю часть выше диагонали. В нижней части табл. 29 даны числовые значения матричных элементов потенциалов для различных полупроводников; причем если | K' – K |2 > 11, то v (K' – K) = v(0) = 0.
Таблица 29
| (000) | v(3) | v(3) | v(3) | v(3) | v(3) | v(3) | v(3) | v(3) | v(0) | v(0) | v(0) | v(0) | v(0) | v(0) |
| (111) | v(0) | v(0) | v(0) | v(8) | v(8) | v(8) | v(0) | v(3) | v(3) | v(3) | v(11) | v(11) | v(11) | |
| (111) | v(8) | v(8) | v(0) | v(0) | v(0) | v(8) | v(11) | v(3) | v(3) | v(3) | v(11) | v(11) | ||
| (111) | v(8) | v(0) | v(0) | v(0) | v(8) | v(3) | v(11) | v(3) | v(11) | v(3) | v(11) | |||
| (111) | v(0) | v(0) | v(0) | v(8) | v(3) | v(3) | v(11) | v(11) | v(11) | v(3) | ||||
| (111) | v(8) | v(8) | v(0) | v(3) | v(11) | v(11) | v(11) | v(3) | v(3) | |||||
| v(3) | v(8) | v(11) | (111) | v(8) | v(0) | v(11) | v(0) | v(11) | v(3) | v(11) | v(3) | |||
| Si | 0.211 | 0.040 | 0.080 | (111) | v(0) | v(11) | v(11) | v(3) | v(3) | v(3) | v(11) | |||
| Ge | 0.269 | 0.038 | 0.035 | (111) | v(11) | v(11) | v(11) | v(3) | v(3) | v(3) | ||||
| Sn | 0.200 | 0.000 | 0.040 | v'(3) | v'(4) | v'(11) | (200) | v(8) | v(8) | v(0) | v(8) | v(3) | ||
| GaP | 0.230 | 0.020 | 0.057 | 0.100 | 0.070 | 0.025 | (020) | v(8) | v(8) | v(0) | v(8) | |||
| GaAg | 0.214 | 0.014 | 0.067 | 0.550 | 0.038 | 0.001 | (002) | v(8) | v(8) | v(0) | ||||
| AlSb | 0.210 | 0.020 | 0.060 | 0.060 | 0.040 | 0.020 | (200) | v(8) | v(8) | |||||
| InP | 0.235 | 0.000 | 0.053 | 0.080 | 0.060 | 0.030 | (020) | v(8) | ||||||
| GaSb | 0.220 | 0.005 | 0.070 | 0.030 | 0.060 | 0.000 | (002) |
Форм-фактор v' (K) учитывает асимметричную структуру цинковой обманки. Знаки минусы в табл. 29 заменены на подчеркивание, например, диагональный матричный элемент (111) следует читать как (–1, 1, –1); для форм-фактора имеем v(3) = 0.211 = –0,211. Зонная структура германия, показанная на рис. 44б, рассчитывалась с помощью матрицы гамильтониана типа табл. 29, но уже размерностью 200 × 200. Существует методика Браста по уменьшению размерности матрицы, изложенная в [1], [51].
В качестве форм-фактора в модели слабой связи берется не сам потенциал иона остова, а некоторое его эффективное значение или псевдопотенциал, который отвечает сглаженной волновой функции. Реальная волновая функция вблизи узлов решетки испытывает сложные быстрые колебания. Но в приближении почти свободных электронов она аппроксимируется плоской волной, один полупериод которой пунктирной линией обозначен на рис. 45.
Рис. 45
Расчетная кривая псевдопотенциала для германия представлена на рис. 46, где нанесены экспериментальные точки его измерения, выполненные в разное время различными авторами. Табл. 30, где приведены семь наборов значений псевдопотенцила и соответствующее им среднеквадратичное отклонение δ точек, рассчитанных по этому методу, от известных экспериментальных точек зоны германия, демонстрирует неоднозначность матричных элементов. Оказалось, что одни и те же уровни энергии с почти одинаковой погрешностью δ получаются при совершенно различных значениях форм-фактора.
Таблица 30
| δ | –v(3) | v(8) | v(11) | v(12) | v(16) | v(19) | |
| Ge(6) | 0.142810 | 0.242104 | 0.022025 | 0.090647 | 0.057899 | 0.000244 | 0.000000 |
| Ge(5) | 0.144739 | 0.244022 | 0.022923 | 0.084844 | 0.068438 | 0.000230 | 0.000000 |
| Ge(4) | 0.144837 | 0.244138 | 0.022801 | 0.085128 | 0.066650 | 0.000000 | 0.000000 |
| Ge(3) | 0.160918 | 0.250481 | 0.000000 | 0.077142 | 0.053759 | 0.000000 | 0.000000 |
| Ge(3) | 0.175624 | 0.249321 | 0.016849 | 0.048291 | 0.000000 | 0.000000 | 0.000000 |
| Ge(3) | 0.177892 | 0.250024 | 0.012851 | 0.000000 | 0.080324 | 0.000000 | 0.000000 |
| Ge(3) | 0.311732 | 0.267218 | 0.000000 | 0.099345 | 0.000000 | 0.000000 | 0.000000 |
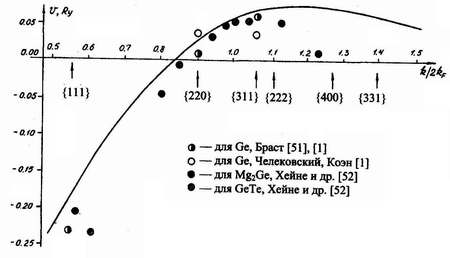
Рис. 46
Широко распространенная система трех значений псевдопотенциала v(3), v(8) и v(11) от трех первых узлов может быть заменена на другой набор псевдопотенциалов: v(3), v(11) и v(12), для которого квадратичная ошибка δ получилась меньшей. Такой выбор форм-фактора оправдывается тем, что теоретически псевдопотенциал v(8) ближе к нулевому значению, чем псевдопотенциал v(12). Подробности расчета можно найти в работе [1], [51].