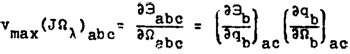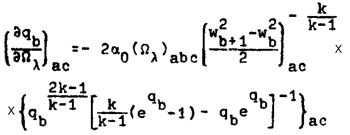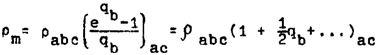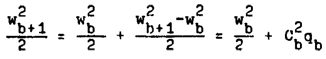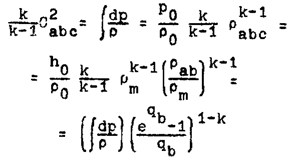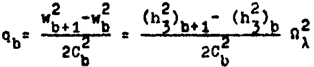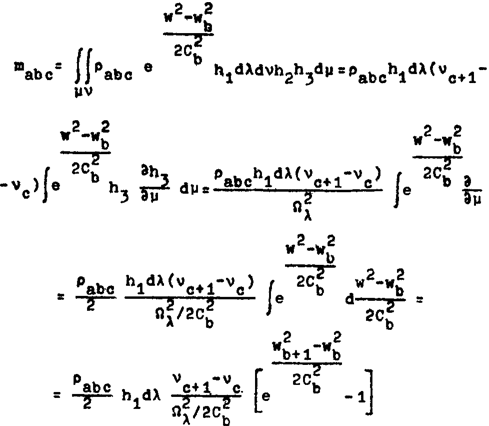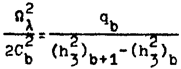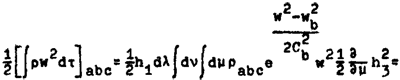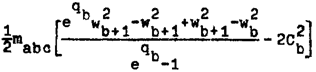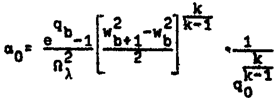Николай Петрович Кастерин (1869-1947) — выдающийся русский физик, предложивший обобщенную теорию аэродинамических и электромагнитных процессов, ученик знаменитого русского ученого А.Г. Столетова, председатель Московского физического общества им. П.Н. Лебедева (1925 – 1930).
Активная научная деятельность Н.П. Кастерина началась в студенческие годы в стенах Московского университета, на физико-математическом факультете, который он успешно закончил в 1892 г. Его оставили в университете для продолжения работы на поприще науки. Уже в год окончания учебы он был удостоен почетной премии им. Мошнина Императорского общества любителей естествознания, антропологии и этнографии. В 1895 г. ему присуждается премия им. А.П. Разцветова физико-математического факультета МГУ, а еще через три года он получает вторую премию им. Мошнина.
С 1896 по 1899 гг. Н.П. Кастерин стажировался в крупнейших университетах Европы, в частности, Берлинском и Лейденском; слушал лекции знаменитых профессоров-исследователей, например, Макса Планка. После возвращения в Россию в качестве доцента он начал преподать различные разделы теоретической физики в Московском университете. В 1906 г. Н.П. Кастерину присуждена — причем минуя степень магистра, что говорит об отсутствии у него карьерных амбиций, — ученая степень доктора физики за глубокое и всесторонне исследование аэродинамических процессов, оформленное в фундаментальный труд под названием «О распространении волн в неоднородной среде. Часть первая. Звуковые волны». В этом же году он избран ординарным профессором кафедры физики Новороссийского университета и одновременно директором Физического института, тесно связанного с этим университетом. В Одессе ему приходилось работать и в других научно-образовательных учреждениях.
В 1922 г. Н.П. Кастерин вновь приезжает в Москву, где работает сначала в Институте биофизики, потом, в качестве высококлассного специалиста и научного эксперта, его приглашают во многие научно-исследовательские институты, в частности, ЦАГИ — крупнейший центр по изучению аэро- и гидродинамики, созданный в 1918 г. великим русским ученым и организатором Николаем Евгеньевичем Жуковским (1847 – 1921). Однако основным местом его работы оставался МГУ. В Москве, по аналогии с Одессой и по европейскому образцу, Н.П. Кастерин сочетает преподавательскую и исследовательскую деятельность. При МГУ создается Научно-исследовательский институт физики (НИИФ) при его самом активном участии.
Первоначально штатный список института насчитывал дюжину ученых: Н.П. Кастерин, А.К. Тимирязев, В.И. Романов, Б.А. Введенский, Н.Е. Успенский, Н.Д. Папалекси, К.П. Яковлев, Н.Н. Андреев, А.Б. Млодзеевский, С.Т. Конобеевский, Г.В. Вульф, В.К. Аркадьев, который в таком небольшом количественном составе проработал почти десять лет. Но в начале 1930-х годов штат института резко увеличился до полусотни человек: вместе с А.С. Предводителевым (1891 – 1973), последовательным сторонником Н.П. Кастерина и А.К. Тимирязева, в состав института были зачислены их активные оппоненты — С.И. Вавилов (1891 – 1951), И.Е. Тамм (1895 – 1971) и т.п.
Таким образом, оплоту московской науки осталось жить недолго. После особого заседания АН СССР, проходившего 9 декабря 1936 г., финансирование НИИФ прекратилось, в начале 1938 г. институт физики, знаменитый своими аэро- и гидродинамическими лабораториями, бережно хранивший великие традиции русской школы Н.Е. Жуковского, был официально введен в подчинение Физического факультета МГУ, а после ухода из жизни его главных вдохновителей и организаторов, Н.П. Кастерина и А.К. Тимирязев, вообще ликвидирован. Более подробно о замечательном русском ученом читайте здесь:
Николай Петрович Кастерин. Жизнь и труды
Ниже приводится развернутый текст первой части доклада
Обобщение основных уравнений аэродинамики и электродинамики
Данный текст книги Н.П. Кастерина был опубликован в малотиражном (510 экз.) сборнике одного из белорусских институтов. Но прежде ознакомьтесь с небольшим предисловием к сборнику, написанным его редактором и составителями А.В. Лыковым, О.Г. Мартыненко и В.А. Бубновым по случаю 80-летия прилежного ученика и верного последователя Н.П. Кастерина — А.С. Предводителева.
Предисловие
Современная гидродинамика основывается на уравнениях Навье-Стокса, установленных в период с 1822 по 1845 гг. Однако современное развитие авиационной и ракетной техники поставило перед исследователями ряд новых задач, связанных прежде всего с высокими скоростями и разряженностью среды. Эти новые задачи вступают в противоречия с исходными предположениями, заложенными при выводе указанных уравнений.
К сожалению, возросшие практические потребности и неотложность их удовлетворения мешают пока спокойному анализу всех недомолвок в обосновании уравнений гидродинамики как для плотных, так и разряженных газов.
Учение об уточнении уравнений Эйлера наиболее остро поставил еще в 1937 году профессор Московского университета Н.П. Кастерин, который подметил, что условия зарождения вихрей в идеальной жидкости связаны прежде всего с возникновением гидромеханических скоростей. Именно разрывной характер скоростей он пытался внести в уравнения идеальной жидкости, после чего уравнения Н.П. Кастерина объяснили процесс образования смерча.
В 1948 году А.С. Предводителев сделал попытку получить уравнения Кастерина методами кинетической теории газов, обратившись к методу Максвелла, позволившему осуществить переход к уравнениям гидродинамики при любой функции распределения. Однако для получения уравнений Навье-Стокса Максвеллу пришлось принять переносные скорости двух сталкивающихся молекул равными, тем самым определив гидродинамическую скорость, как скорость теплового движения атомов или молекул. Устранив ограничения этой гипотезы, А.С. Предводителев выполнил обобщение уравнений вязкой жидкости, причем уравнения Навье-Стокса, Кастерина и Эйлера вытекают из них как частный случай.
Изложенное выше и определило тематику предлагаемого сборника.
Обобщение основных уравнений
аэродинамики и электродинамики
(Аэродинамическая часть)Н. П. Кастерин
Проблемы физической гидродинамики / Сборник статей под ред. академика АН БССР А.В. Лыкова. – Минск: Институт тепло- и массообмена АН БССР, 1971, с. 268 – 308. (Сборник посвящен 80-летию научной и педагогической деятельности чл. - корр. АН СССР А.С. Предводителева.)
1. Обобщение аэродинамики Эйлера
При нашем исследовании мы будем опираться на основные представления кинематической теории газов и на установленные его закономерности, однако ограничимся исследованием движения только при условии неразрывности. Это ограничение позволит нам пользоваться методом аналитической механики, в противном случае, если условие неразрывности не имеет места, исследование движения газа возможно лишь методами статистической механики. Но и в случае неразрывности нам придется прибегнуть отчасти к статистической механике, выражая условие неразрывности движения газа в виде требования, чтобы масса газа, заключенная внутри некоторой одно-связанной замкнутой поверхности оставалась во все время движения неизменной, т.е.
, (1)
где ρ — плотность газа, τ — объем газа внутри поверхности. Мы прежде всего сталкиваемся с вопросом, какой объем газа может быть принят за элементарный. Принимая газ за непрерывную жидкость, как это делается в теории Эйлера, мы можем считать объем τ сколь угодно малым. С точки зрения кинетической теории газов, в которой, вследствие молекулярной структуры газа, величина скорости в данной точке газа плотностью ρ, при температуре Т, упругости р является величиной средней статистической, бесконечно малый объем неприемлем.
За элементарный объем мы примем объем некоторой минимальной массы, для частей которой уже не может иметь место условие неразрывности (1), т.е. внутри которой движение газа определяется законами статистической механики. При дальнейшем анализе мы предполагаем, что объем так определенной «аэродинамической частицы» настолько мал, что уравнение неразрывности для нее может быть выражено приближенно в обычной дифференциальной форме без введения вторых производных.
Движение газа в каждой точке характеризуется скоростью «видимого» (по терминологии Гельмгольца «стройного») движения. Эта скорость V определяется как статистическая средняя скорость молекул, находящихся вокруг рассматриваемой точки и имеющих всевозможные по величине и направлению скорости. Величина и направление видимой скорости V зависит от закона распределения молекул по скорости и может изменяться только с изменением этого распределения. Таким образом, может случиться, что в рассматриваемой точке внутри газа в данный момент нет ни одной молекулы, но тем не менее мы можем говорить о скорости V в этой точке и в этот момент. Из этого видно, что, несмотря на прерывную молекулярную структуру газа, можно говорить о непрерывности в пространстве и во времени скорости V, определенной статистически.
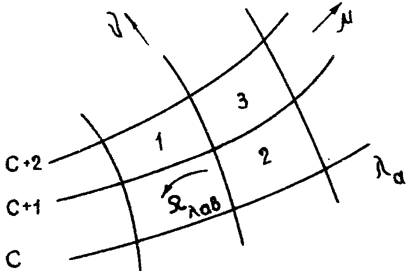
Рассмотрим вихревое движение газа. За оси координат примем криволинейные, трижды ортогональные координаты λ, μ, ν, причем λ определяется направлением вихря, угловая скорость которого Ωλ; направление ν — направлением составляющей скорости w, нормальной к вихрю; направление μ перпендикулярно к направлению λ и ν составляет с ними правую систему координат, так что нормальная составляющая скорости —
, а продольная составляющая скорости —
и
,
— коэффициенты Ламе (примечание автора 1), (рис. 1, 2).
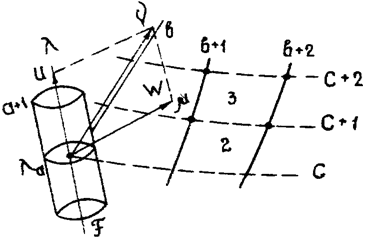
Рис. 1.
Рис. 2. Схема «аэродинамических ячеек»
Разобьем массу движущегося газа на ячейки соответствующими координатными плоскостями таким образом, чтобы каждая ячейка представляла «аэродинамическую частицу», т.е. чтобы движение газа внутри ячейки определялось по законам статистической механики. Пусть рис. 1 представляет схематически координатную сетку на поверхности λa = const, по нормали к которой направлена ось вихря. Ячейки, соответствующие узлам решетки, пронумерованы индексами a, a + 1, a + 2, ...; b, b + 1, b + 2, ...; c, c + 1, c + 2, ....
Если Ωλ — угловая скорость вихря в какой-либо из ячеек, то скорости должны удовлетворять условию
,
,
.
Предположим ячейки достаточно малыми, тогда можем Ωλ считать внутри каждой ячейки постоянной и из этих уравнений будем иметь уравнение непрерывности вихря в виде
, (2)
где σλ — площадь сечения ячейки, нормального к λ.
Далее, так как дλ произвольно мало, то можно пренебречь изменениями
и
с изменением λ внутри ячейки. Тогда получается, что
и, следовательно,
,
,
, при
находим
,
.
Распределение массы вращающейся ячейки дает закон Больцмана (прим. автора 2):
(3)
где n означает число молекул в единицах объема, в nabc — в узле сетки abc, и (
) представляет квадрат наивероятнейшей скорости молекулы, тогда как
есть средний квадрат молекулярной скорости в каком-либо одном направлении или квадрат скорости звука, вычисленной по формуле Ньютона, т.е.
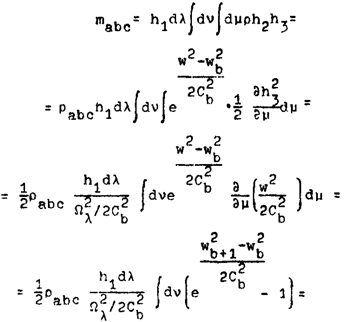
. Здесь R — газовая постоянная, а T — абсолютная температура газа в ячейке. Вычисляя при помощи (3) массу газа в ячейке, получаем (прим. автора 3) формулу
. (4)
Для краткости обозначим
,
тогда средняя плотность
. (5)
Для составления уравнения движения вихря газа в форме Лагранжа-Гельмгольца необходимо знать энергию газа в каждой ячейке и кинетический потенциал.
Энергия молекулярных движений газа на единицу массы составляется из тепловой энергии, равной
(где cV — теплоемкость идеального газа при постоянном объеме, T — абсолютная температура), и энергии «давления» будет равна
,
здесь cp — теплоемкость газа при постоянном давлении. Следовательно, полная энергия молекулярных давлений будет равна
или
, (6)
где k — адиабатная постоянная.
Эту энергию Э можно также представить в виде зависимости от упругости и плотности газа (прим. автора 4):
. (7)
Кинетическая энергия видимого движения газа в ячейки равна
или (прим. автора 5)
. (8)
Таким образом, полная энергия как молекулярных движений, так и видимых выражается в форме
(9)
или также в форме [см.: (4) и (7)]
. (9*)
Рассматривая выражение энергии в форме (9), видим, что она состоит из кинетической энергии молекулярных движений
, кинетической энергии видимого движения
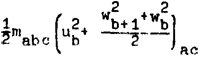
И, наконец, кинетической энергии вращающегося движения газа с угловой скоростью Ωλ:
.
В самом деле, так как
,
то этот последний член в выражении энергии можно представить в виде
(10)
Приступая к составлению движения газа, выясним, какими параметрами определяется система движущихся «аэродинамических частиц». Для каждой аэродинамической частицы должно выполняться условие неразрывности (1). В это условие входят только компоненты скорости на поверхности, ограничивающей частицы, их производные и координаты этой поверхности. Поэтому это условие правильно называть условием неразрывности оболочки «аэродинамической частицы».
Для удовлетворения условия неразрывности оболочки необходимо допустить, что при переходе изнутри «частицы», где условие (1) не имеет места, на поверхности ее при непрерывном изменении компонентов скорости u и w производные от (
)a и (
)c по координатам могут вообще изменяться прерывно. Соответственно этому должны прерывно изменяться и производные по координатам от функции Ламе. Чтобы отметить эту особенность компонент скорости оболочки, будем в случае надобности обозначать функции Ламе и скорости
и
для внутренних частей «аэродинамической частицы» звездочкой. Например,
, а для самой оболочки оставим прежние обозначения, т.е.
,
и т.д.
Выражение для полной энергии «частицы» (9) легко можно преобразовать следующим образом; так как
,
то мы получаем из (9)
(11)
Как видно из выражения (4) для
, qb есть функция Ωλ и
.
Кинетический потенциал системы Н = П – К в данном случае равен Н = – Э (12), так как вся энергия есть кинетическая.
Поэтому для кинетической системы вихрей получаем
. (13)
Составим прежде всего дифференциальное уравнение движения для (Ωλ)abc :
,
оно сводится к уравнению
,
выражающему неизменность во времени количества вращательного движения (JΩ)abc для каждой «аэродинамической частицы»
при условии, конечно, что mabc остается неизменным. Из выражения (11) для Эabc получаем
.
Можно получить такое равенство:
(14)
где через α0 обозначена величина
.
Теперь из выражения (14) находим
Таким образом,
. (15)
Выражение (14) можно преобразовать так:
(14*)
где краткости ради обозначено
.
Тогда окончательно получим для количества вращательного движения «частицы» следующее выражение:
. (15*)
Из (14*) видим, при k = 2 qb представляет только функцию от n и не зависит от Ωλ.
Итак, из
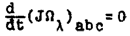
следует, что для всех газов, так как для них k < 2 напряжение вихря
есть функция угловой скорости Ωλ и оно не сохраняется. Только при k = 2 для сверхгаза мы получаем сохранение напряжения вихря, т.е.
. (16)
При этом предполагается, что
. Из состава для α0 мы видим, что не только должно быть
,
но также
. (1*)
Последнее условие удовлетворяется тождественно.
Из (1) и (1*) следует, что
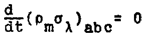
и также
. (1**)
Составляя уравнения движения системы вихрей, будем предполагать в дальнейшем, что имеем дело с простейшим случаем — сверхгазом, для которого имеет место уравнение (16).
Далее предположим, что
или
— малые величины по сравнению с единицей, так что в выражении для кинетического потенциала можно ограничиться членами только порядка qb, отбрасывая все остальные члены высшего порядка.
Возьмем для энергии в ячейке выражение в форме (9) при k → 2. Энергия всей системы вихрей равна
.
Так как λabc не входит в это выражение, а только
abc , потому что
, то этот параметр — безразмерный (циклический). Далее заметим, что Ωλ, на основании уравнений неразрывности вихря (2) и сохранения напряжения вихря (16), есть функция только координатных параметров, поэтому и qb зависит только от последних.
Таким образом, при составлении выражения для кинетического потенциала в выражении для Э надо изменить знак на минус только у члена, содержащего w2, причем надо отметить, что
.
Итак, кинетический потенциал всей системы имеет вид
, (18)
причем параметрами системы будут все прежде указанные, за исключением всех
abc.
Кинетический потенциал отдельной «частицы» равен
. (18*)
Последнее выражение для однородной системы можно переписать так:
. (18**)
Вывод дифференциального уравнения движения вихрей совершенно аналогично, как это было сделано в электродинамике, получаем из (18**)
,
(19)
и уравнение связи
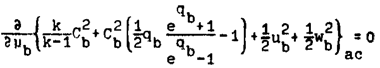
или на основании первого из уравнений (19)
, (20)
и qb << 1 с точностью до величины порядка q2b. При k = 2 и для случая qb << 1 система (19) примет вид
(19*)
При k + 2 и qb << 1 можно получить еще другую группу уравнений, содержащих Ωλ, если исходить из выражения для кинетического потенциала в форме (18) и вспомнить, что
и
Таким образом, приближенно, с точностью до величины порядка q2b кинетический потенциал принимает вид
(20*)
Составим дифференциальное уравнение, переходя к предельному случаю k = 2 и замечая на основании (1) и (1**), что
и
могут быть опущены в дифференциальных уравнениях как постоянные. В результате на основании (19) искомые уравнения принимают вид, если учесть, что
,
,
. (21)
Уравнение связи при этом можно записать в виде
. (22)
Из уравнений (19*), (21) и (22) видим, что деформации и движение в вихревом поле определяется в зависимости от координат и скоростей в узловых точках координатной сетки. Эти узлы не могут быть сближены как угодно близко, так как объем «аэродинамической частицы» хотя и мал, но не может быть выбран произвольно малым, по крайней мере, это относится к размерам сечения вихря, нормального к его направлению.
Преобразовывая уравнения вихревого поля аналогично тому, как это сделано для электромагнитного поля, и по тем же основаниям, найдем следующую систему, если введем обозначение для 2C2b, представляющей квадрат адиабатной скорости звука для сверхгаза, как C2 и отбрасывая все индексы:
,
, (23)
.
Для безвихревого газа, т.е. когда rotV = 0, выполняется условие VrotV = 0. Поэтому мы могли бы, применяя трижды ортогональную систему натуральных криволинейных координат λ, μ, ν, принять за направление λ направление скорости V, а μ и ν направить нормально к λ в каких-либо двух произвольных, взаимно перпендикулярных направлениях. Но в силу того, что потенциальное течение газа управляется теми же вихрями, которые расположены на его границах, например на твердых стенках, ограничивающих газ, в дальнейшем изложении мы отнесем потенциальное движение к осям λ, μ, ν, относительно которых скорость V распадается на два компонента:
и
, а
.
Энергия молекулярных движений газа выразится в форме (6)
, (24)
где
— масса «аэродинамической частицы» abc.
Кинетическая энергия в простой форме
. (25)
Параметрами, определяющими энергию системы, являются прежние
для всех возможных значений индексов.
Кинетический потенциал системы «аэродинамических частиц» принимает вид
, (26)
причем pabc (упругость газа) и ρabc (его плотность) представляют функции только соответствующих координатных параметров и не зависят от скоростей
и
.
Составим основное дифференциальное уравнение движения газа в форме уравнения Лагранжа — Гельмгольца:
.
Теперь, принимая qa последовательно равным
,
легко находим при условии (1)
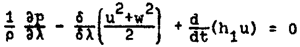
(27)
.
Для ясности здесь обозначены через д/дλ производные по соответствующим параметрам в предположении, что скорости
и
. остаются неизменными.
Уравнения (27) по виду вполне совпадают с уравнениями Эйлера для криволинейных координат. Но подобно тому, как это было выяснено в первой главе, вследствие конечности размера «аэродинамической частицы», мы должны при выводе производные
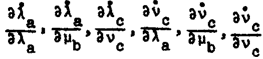
считать равными нулю, и тогда не будет никакой разницы между
и
и т.д.
Таким образом, уравнения аэродинамики в координатной форме напишутся, если еще ввести адиабатную скорость звука C, в окончательном виде:
(28)
2. Примечание автора
1. Возможность координат λ, μ, ν обусловлена тем обстоятельством, что в газе не может быть «закручивания». Аналитически это выражается дифференциальным уравнением ΩrotΩ = 0 (см. например, Bjerkness "Phys. Hydrodyn." Berlin, 1933 j. s. 7).
2. Сравни Maxwell "Scientific Papers", vol. 11, p. 739.
3.
.
4.
5. Давление, касающееся пограничных условий.
В том случае, когда система вихрей окружена незавихренным газом, на границе между завихренной частью газа и незавихренной должны быть выполнены условия, которые вытекают из основного уравнения (1), которое применительно к данному случаю будет иметь вид
. (29)
Здесь Fqa — сила, соответствующая параметру qa и действующая на границе раздела.
Составим эти условия на свободных концах вихрей. Возьмем кинетический потенциал в первоначальном виде
,
где для краткости обозначено
.
Составляя уравнение (29) для параметра
, получим
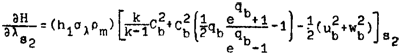
далее
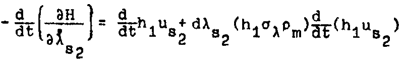
Первый член в последнем выражении, содержащий множитель
, был бы равен нулю, если бы для конца вихря было бы справедливо уравнения неразрывности, но из выражения
видим, что
,
т.е.
не есть постоянная величина для конца вихря. Мы можем для пограничной «частицы», лежащей частично в вихревой области и частично в невихревой, требовать, чтобы ее масса оставалась неизменной, т.е.
, (30)
где ρ' и τ' — плотность и объем соответствующей «частицы» в невихревой области, так как масса ρmτ завихренной части «частицы» тоже не сохраняется.
Другими словами, граница между вихревой частицей газа и невихревой на конце вихря проходит внутри частицы. При указанных обстоятельствах представить
. (31)
Таким образом, уравнение (30) принимает вид в рассматриваемом случае
. (32)
Составляя уравнение (29) для невихревой «частицы», входящей в рассматриваемую пограничную смежную «частицу», находим на основании (30)
. (33)
Чтобы сила
, производимая незавихренной частью газа из завихренной, была равна нулю, необходимо по (32), чтобы
. (34)
Так как при этом условии величина кинетического потенциала завихренной «частицы» сделалась бы отрицательной и равной
,
то необходимо, чтобы еще
.
Тогда уравнение на конце вихря принимает вид
, (35)
где обозначено
.
Так как по третьему закону Ньютона
, то из (33) для
получается
. (36)
В силу непрерывности скорости
,
, поэтому из (35) и (36) выходит
и при k = 2 пограничное условие на свободном конце вихря имеет вид
, где
. (35*)
Так как кинетический потенциал
для «частиц», лежащих в пограничном слое, постоянен и равен нулю, то уравнение (29) для параметров
и
обращается в тождество. Для боковой границы
уравнение (29) дает для завихренного поля
, (37)
а для незавихренного
, (38)
причем кинетический потенциал в этом случае взят в виде
.
Если
и, следовательно,
равен нулю, то из (37) и (38) вихревые производные через конечные разности находим в виде
, (37*)
. (38*)
Так как по непрерывности
и
, то
(39)
или для k = 2
. (39)
Если кроме того,
,
то
. (40)
Второе уравнение для параметра
для этой пограничной частицы обращается в тождество.
3. Примечание проф. А.К. Тимирязева
1. В тексте сказано: "Так как dλ произвольно мало, то можно пренебречь изменениями
и
с изменением λ внутри ячейки». Отсюда следует
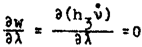
или
.
Так как аэродинамическая частица движется как целое, то
, и тогда из полученного равенства заключаем, что
и
. Поэтому из второго и третьего уравнений системы
,
,
,
находим
и
,
откуда, так как
и
(«аэродинамическая частица» движется как целое: поле ведь состоит из дискретных вихревых трубок), получается
и
.
Далее рассмотрим связь между
и угловой скоростью Ω и также выражение для площади σλ и для объема τ «аэродинамической частицы».
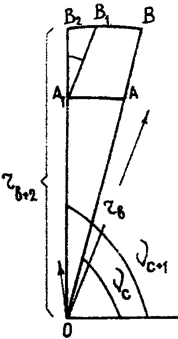
Рис. 3. Схема перемещения «аэродинамической ячейки»
Пусть АВ перемещается А1В2 (рис. 3). Это перемещение достигается одним вращением вокруг оси «0», которое состоит из поступательного перемещения из АВ в А1В1 и вращения вокруг А1, так что совершается перемещение из АВ в АВ. Если совершается поворот вокруг «0» из А1В1 в А1В2, то угол при «0» и при А1 будет
. Но поворот вокруг А1 и есть Ω. Итак,
. Далее подсчитаем площадь
.
В первом приближении криволинейную систему координат можно рассматривать как цилиндрическую. Дуга, соответствующая координате ν, будет
, откуда
. Координате μ соответствует
,
; а тогда
.
Но это вытекает из рис. 2 для цилиндрических координат, если подсчитать АВА1В2 :
.
Отсюда легко получается объем «аэродинамической частицы» τ :
.
2. Прим. к уравнениям (4) и (5).
Можно преобразовать формулу для qb, замечая, что
и
.
Теперь имеем
или
,
откуда
.
Вычисляем далее
Но из определения qb мы видим
и тогда
,
т.е. выражение (5) в тексте.
3. Прим. к уравнению (7)
Так как
, то величина
будет равна
,
где R — универсальная газовая постоянная, отнесенная к молекулярному весу.
Теперь выражение (7) получается следующим образом:
или согласно (5)
,
откуда
,
что приводит к выражению (7).
4. Прим. к уравнению (8).
.
Далее вычисляем следующим образом:
,
затем
,
таким образом,
. (а)
Рассмотрим теперь различные виды выражения кинетической энергии. Полученное нами выражение (а) можно представить иначе:
или
(а')
или можно представить еще следующим образом:
, (а'')
Взяв среднюю арифметическую из (а штрих) и (а''), получим выражение (8).
5. Прим. к уравнению (10)
Полная энергия равна
,
что совпадает с уравнением (9). Эту же энергию можно представить [см. (4) и (5)] в виде
.
Теперь докажем, что
— энергия вращательного движения. Действительно,
.
6. Прим. к уравнению (11)
Ранее нами получено выражение
,
и там же мы имели
.
Вставим в первое из этих уравнений
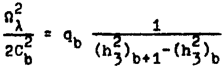
и будем обозначать для внутренних частей τ соответствующие величины звездочками сверху, тогда будем иметь
.
Далее произведем замену
.
Предварительно докажем это. Действительно,
или
.
Точно так же
,
т.е.
,
откуда
, а
,
что и требовалось доказать.
Итак,
,
откуда
.
Полагая левую часть α0, имеем
.
Заменяя в полученном выражении
,
находим
или
.
Таким образом, qb есть функция Ωλ,
и α0.