Дж. Дж. Томсон

Электричество и материя

Под редакцией проф. А.К. Тимирязева и З.А. Цетлина
с предисловием проф. А.К. Тимирязева и его приложениями
Перевод с 5-го англ-го изд-я 1924 г. С. Давыдова И Н. Лихтгейма
Гос. изд-во Москва — Ленинград — 1928.

Книга Дж. Дж. Томсона «Электричество и материя» составлена из лекций, прочитанных автором в 1903 году. Текст публикуется на нашем сайте с сокращениями, тем не менее, книга остается прекрасным учебным пособием для выработки у будущих физиков конструктивных навыков мышления. Автор рассказывает о многих физических понятиях, которые сегодня уже во многом утратили свое первоначальное наглядное представление. Так, например, он раскрывает тайну появления на свет «релятивистских» формул для массы и энергии (E = mc²).

Предисловие проф. А.К. Тимирязева

Книга Дж. Дж. Томсона "Электричество и материя", появившаяся в 1903 году, сохраняет все свое значение и в настоящее время. Она представляет собой доступное изложение взглядов автора на строение электромагнитного поля. Максвелловская теория электромагнитного поля обыкновенно изображается как перевод великих идей Фарадея на современный математический язык. Теория Томсона представляет собой также перевод, но гораздо более близкий к подлиннику.

Оригинальные работы Дж. Дж. Томсона были напечатаны в промежуток времени от 1880 года до наших дней: они представляют собой одно стройное целое, поэтому появившиеся в 1924 и 1925 году замечательные работы Томсона, дающие синтез волновой и квантовой теории света, остались незамеченными, так как, будучи оторваны от всех предшествующих работ, они кажутся изобилующими всякими произвольными допущениями. На самом же деле они находятся в стройной логической связи с тем, что было найдено Томсоном раньше и что, невидимому, основательно забыто.

Книга "Электричество и материя" дает, как мы уже сказали, в сжатой и доступной форме основные взгляды Томсона на электромагнитное поле, которые сохранили все свое значение в наши дни, устарели лишь некоторые части V и VI глав, где речь идет о строении атома; к этим главам сделаны соответствующие примечания редакции. В качестве приложения к этой части дан перевод речи Дж. Дж. Томсона "Материя и эфир". Вторая часть книги посвящена опубликованной в 1924 году замечательной работе Томсона "Структура света" и связанным с этой работой вопросам. По Томсону квант света представляет замкнутую кольцеобразную фарадеевскую силовую линию или, как предпочитает выражаться Томсона, "световой квант есть замкнутая фарадеева трубка". Свойства этих световых квант поразительно сходны со свойствами вихревых колец, поэтому в качестве приложения к этой части книги даны статья проф. Н.Е. Жуковского "Основы учения о вихрях", Вильяма Томсона (Лорда Кельвина) "О вихревом атоме" и статьи 3.А. Цейтлина, посвященные истории и методологии вихревой теории материи. В конце книги приложен перевод первой главы из сочинений Томсона "Новейшие исследования в области электричества и магнетизма", где дается изложение взглядов Томсона, но уже в математической форме. Читатель, владеющий элементами математики, сейчас же увидит из этой статьи, насколько прочно обоснованы взгляды Томсона и насколько близка его теория электромагнитного поля к той картине, которую представлял себе Фарадей.

В заключение необходимо напомнить, что Томсон, работая изложенным в настоящей книге методом, первый пришел к понятию электромагнитной массы в 1881 году, первый установил изменение этой массы со скоростью, и притом данное им этим явлениям объяснение было обосновано на строго материалистической почве. Работы Томсона в то время остались незамеченными. Через 20 — 25 лет после работ Томсона понятие об электромагнитной массе стало выдвигаться на первый план, но, вследствие формального подхода тогдашних теоретиков, те же самые взгляды, которые были высказаны Томсоном, были изложены на идеалистический лад и привели к выводам о дематериализации материи. Блестящая материалистическая критика этого идеалистического учения дана у Ленина в 5 главе "Материализма и эмпириокритицизма". Весьма характерно, что в последние годы трудности, на которые натолкнулась так называемая теория квант, привели к новой вспышке идеализма в физике, и в этой области мы видим опять, как Томсон пришел к синтезу основного противоречия теории квант и опять на строго материалистической почве. Уже по этой одной причине изложенные в настоящей книге взгляды Томсона заслуживают самого серьезного внимания тех, кто интересуется методологическими проблемами современного естествознания.

А. Тимирязев.
27/V 1927 г.

Предисловие Дж. Дж. Томсона

В этих лекциях, читанных в Yale University в мае 1903 г., я сделал попытку рассмотреть значение последних успехов в области учения об электричестве для наших понятий о строении материи и природе электричества; последние вопросы, вероятно, настолько тесно связаны друг с другом, что решение одного из них дало бы решение другого. Характерной особенностью новейших изысканий в области электричества, как изучение и открытие катодных и рентгеновых лучей, радиоактивных веществ является то обстоятельство, что они указывают на тесную связь между материей и электричеством.

Избирая эту связь предметом "Лекций памяти Silliman'a", мне казалось, что размышления о значении для этой связи последних работ в области электричества имеют тем большее значение, что такого рода рассмотрение возбуждает множество вопросов, которые могли бы служить некоторым из моих слушателей замечательными объектами для новых изысканий.

Дж. Дж, Томсон.
Кембридж.
Август. 1903 г.

Глава I. Изображение электрического поля при помощи силовых линий

Предметом настоящих лекций будет изложение в простой и насколько возможно элементарной форме некоторых теорий, относящихся к природе электричества, к процессам, имеющим место в электрическом поле, к связи между электрической материей и обыкновенной, связи, на которую дают указания результаты последних исследований.

Прогресс науки об электричестве был сильно облегчен, благодаря чисто теоретическим рассуждениям о природе электричества. В самом деле, едва ли возможно переоценить услуги, которые были оказаны двумя теориями, которые так же стары, как и сама наука; я имею в виду теории, известные под именами дуалистической и унитарной теории электричества.

Дуалистическая теория объясняет явлений электростатики, исходя из положения, что в природе существуют две несоздаваемые вновь и неуничтожаемые жидкости, присутствие которых вызывает электрические явления. Одна из этих жидкостей называется положительным электричеством, другая — отрицательным электричеством; электрические явления могут быть объяснены, если приписать этим жидкостям следующие свойства. Частицы положительного электричества взаимно отталкиваются с силами, изменяющимися обратно пропорционально квадрату расстояния между ними, точно так же, как и частицы отрицательного электричества. С другой стороны, частицы положительного электричества притягивают частицы отрицательного электричества. Притяжение между двумя зарядами противоположных знаков m и m', по одному варианту этой теории, принимается в точности равным отталкиванию между двумя зарядами m и m' одного и того же знака, находящимися в тех же местах, что и предыдущие. По другому варианту этой теории принимается, что притяжение немного превышает отталкивание; это дает основание для возможности объяснения сил тяготения.

Жидкости предполагаются чрезвычайно подвижными и способными проходить с большой легкостью сквозь проводники. Электрическое состояние тела определяется разностью между количествами двух электрических жидкостей, в нем содержащихся; если тело содержит положительной жидкости больше, чем отрицательной, оно наэлектризовано положительно; если же оно содержит равные количества, оно не заряжено. Так как жидкости не могут быть ни созданы ни уничтожены, то появление положительной жидкости в одном месте должно сопровождаться исчезновением такого же количества в другом месте, так что получение электричества одного знака должно сопровождаться получением такого же количества электричества противоположного знака.

Согласно этой теории, любое тело состоит из трех веществ: обыкновенной материи, положительного электричества и отрицательного. Принимается, что последние действуют каждое само на себя и одно на другое, но в первоначальном варианте этой теории не предполагалось, что между обыкновенной материей и электрическими жидкостями существует взаимодействие; только в недавнее сравнительно время Гельмгольц ввел в науку идею о специфическом притяжении между обыкновенной материей и электрическими жидкостями. Он сделал это с целью объяснить явление контактной электризации (т.е. так называемую электризацию при соприкосновении), состоящее в том, что, когда два металла, напр., цинк и медь, приведены в соприкосновение, то происходит разделение электричеств, причем цинк электризуется положительно, медь — отрицательно. Гельмгольц предположил, что между обыкновенной материей и электрическими жидкостями действуют силы, которые изменяются для различных видов материи; так, положительное электричество сильнее притягивается цинком, чем медью, так что, если привести в соприкосновение эти металлы, цинк отнимает у меди некоторое количество положительного электричества.

В дуалистической теории есть некоторая неопределенность, которая может быть иллюстрирована рассмотрением ненаэлектризованного тела. Дуалистическая теория говорит нам только то, что тело содержит одинаковые количества той и другой жидкости. Она не дает нам никаких указаний на количество каждой из жидкостей, она предполагает только, что если равнее количества двух жидкостей прибавлены к телу, последнее не подвергнется никаким изменениям, так как равные количества двух жидкостей совершенно нейтрализуют друг друга. Если рассматривать эти жидкости как нечто более вещественное, чем математические символы « + » и « – », мы встретимся с затруднениями. Если мы будем их рассматривать, например, как физические жидкости, мы вынуждены будем предположить, что смесь двух жидкостей в одинаковых количествах есть нечто настолько лишенное физических свойств, что самое присутствие смеси никогда не может быть обнаружено.

Вторая теория, унитарная теория Вениамина Франклина, свободна от этого упрека. Согласно этой теории, есть только одна электрическая жидкость — положительная; роль другой жидкости принимает на себя обыкновенная материя, частицы которой взаимно отталкиваются и притягивают положительную жидкость точно так, как это делают частицы отрицательной жидкости по дуалистической теории. Ненаэлектризованная материи предполагается соединенной с таким количеством электрической жидкости, что притяжение материей какой-либо внешней по отношению к ней электрической жидкости как раз таково, что уравновешивает отталкивание этой внешней электрической жидкости тою жидкостью, которая соединена с самой материей. С этой точки зрения, если количество материи в теле известно, количество электрической жидкости является также определенным.

Услуги, которые теории жидкостей оказали учению об электричестве, не зависят от понятия о жидкости, как о чем-то, обладающем определенными физическими свойствами. Жидкости были математическими фикциями, служившими для того, чтобы локализировать определенным образом притяжения и отталкивания между наэлектризованными телами; они явились средством, при помощи которого блестяще развитая теория сил, изменяющихся обратно пропорционально квадрату расстояния, теория, внушенная открытием тяготения, могла быть приложена к электрическим явлениям. До тех пор, пока мы ограничиваемся вопросами, которые вытекают из закона взаимодействия между наэлектризованными телами и явлениями одновременного возникновения равных количеств положительного и отрицательного электричества, обе теории должны давать одинаковые результаты, и нет ничего, что заставило бы сделать между ними выбор.

Те физики и математики, которые больше всех способствовали развитию теорий жидкостей, ограничивались вопросами такого рода; при этом они до такой степени утончали и идеализировали понятие об этих жидкостях, что всякий намек на их физические свойства стал почти неделикатным. Только при изучении явлений, касающихся физических свойств жидкости, мы можем надеяться сделать выбор между двумя соперничающими теориями. Возьмем случай, действительно, имевший место. Нам удалось измерить массы, соединенные с данными электрическими зарядами в газах при низких давлениях; при этом оказалось, что масса, соединенная с положительным зарядом, неизменно больше массы, соединенной с отрицательным зарядом. Эту разницу мы должны были бы ожидать согласно унитарной теории Франклина, если ее видоизменить так, чтобы электрическая жидкость соответствовала отрицательному электричеству вместо положительного, между тем как у нас нет никаких оснований ожидать такой большой разницы с точки зрения дуалистической теории. Я уверен, что мы будем поражены сходством между некоторыми воззрениями, к которым привели нас самые последние открытия, и теми, которые установил Франклин, когда наша наука была еще в младенческом состоянии.

Теория силовых линий Фарадея

Теории жидкостей, по самой природе своей, заключают в себе идею о действии на расстоянии. Хотя эта идея была принята большинством математиков, вследствие ее пригодности для математического анализа, многие великие физики чувствовали, что они не могут ее принять и посвятили много размышлений и труда на то, чтобы заменить ее чем-нибудь заключающим в себе механическую непрерывность. Самым выдающимся из них был Фарадей. Фарадей был глубоко убежден в аксиоме или, если хотите, в догме, что материя не может действовать там, где ее нет. Фарадей, обладавший, по моему, несравненной математической проницательностью, не владел анализом, так что удобство идеи о действии на расстоянии для целей вычислительных не имело возможности ослабить то отвращение, которое он испытывал к идее сил, действующих далеко от их источника и не имеющих физической связи с этим источником. Поэтому он искал способа представления действий в электрическом поле, который был бы свободен от идеи действия на расстоянии и заменил бы ее такой, которая выдвинула бы на первый план непрерывную связь, существующую между взаимодействующими телами. Ему удалось это сделать введением понятия о силовых линиях, Так как я буду постоянно пользоваться этим методом и так как, по моему убеждению, его могущество и возможности не были никогда достаточно выявлены, я посвящу несколько времени изложению и развитию такого представления об электрическом поле.

К этому методу Фарадея привело рассматривание силовых линий вокруг магнитного бруска. Если железные опилки рассыпать на гладкой поверхности около магнита, они сами расположатся, как на рис. 1; на нем хорошо видны линии, идущие от одного полюса магнита к другому; направление этих линий в каждой точке совпадает с направлением магнитной силы, между тем как напряженность силы указывается густотой линий. Отправляясь из какой-нибудь точки тюля и двигаясь все время по направлению магнитной силы, мы проведем линию, которая не прервется, пока мы не дойдем до отрицательного полюса магнита; если такие линии будут проведены через все точки поля, пространство, в котором расположено магнитное поле, будет заполнено системой линий, придающей ему волокнистое строение, в роде того, которое имеет стог сена или соломы, причем волокна расположены вдоль силовых линий.

Рис. 1

До сих пор я говорил о линиях магнитной силы; эти же рассуждения могут быть применены к электрическому полю, и мы можем рассматривать электрическое поле, как наполненное линиями электрической силы, начинающимися на положительно наэлектризованных телах и оканчивающимися на отрицательно наэлектризованных.

До этого пункта ход рассуждений был чисто геометрический и мог бы быть принят также и теми, кто смотрит на вопрос с точки зрения действия на расстоянии. Для Фарадея, однако, линии сил были чем-то большим, чем математические абстракции, они были физическими реальностями. Фарадей материализовал силовые линии и наделил их электрическими свойствами для того, чтобы объяснить явления электрического поля. Так, он предположил, что они находятся в состоянии натяжения и отталкиваются друг от друга. Вместо неосязаемого действия на расстоянии между двумя наэлектризованными телами, Фараде и рассматривал все пространство между телами наполненным натянутыми и взаимно отталкивающимися пружинами. Электрические заряды, интерпретацию которых только и давали теории жидкостей, были с этой точки зрения концами этих пружин, и электрический заряд, вместо того, чтобы быть некоторым количеством жидкости, заключенным в наэлектризованном теле, являлся обширным арсеналом пружин, простиравшихся по всем направлениям во все части поля.

Чтобы пояснить нашу идею в этом пункте, рассмотрим несколько простых примеров с точки зрения Фарадея. Возьмем сначала случай с двумя телами, обладающими равными и противоположными зарядами; расположение силовых линий показано на рис. 2.

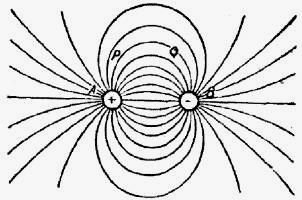
Рис. 2

Вы замечаете, что силовые линии гуще всего вдоль прямой АВ, соединяющей тела, и что больше силовых линий с той стороны А, которая ближе к В, чем с противоположной. Рассмотрим действие этих силовых линий на А. Линии находится в состоянии натяжения и тянут А в разные стороны; но так как со стороны, ближайшей к В, на А действует больше силовых линий, чем с противоположной, то притяжение от А к В преодолевает притяжение в противоположную сторону, поэтому А будет стремиться двигаться к В. Таким образом Фарадей представлял себе притяжение между двумя противоположно наэлектризованными телами.

Рассмотрим теперь состояние, в каком находится какая-нибудь криволинейная силовая линия, напр., PQ. Она находится в состоянии натяжения и стремится поэтому сама выпрямиться. Что ей мешает сделать это и удерживает ее в равновесии в изогнутой форме? Мы найдем объяснение этому, если вспомним, что силовые линии отталкиваются друг от друга и что они сосредоточены в большем числе в области между PQ и АВ, чем по другую сторону от PQ. Таким образом, отталкивание линий внутри PQ больше отталкивания внешних линий, и линия PQ будет поэтому выгнута наружу.

Перейдем теперь от случая двух противоположно наэлектризованных тел к случаю двух тел, наэлектризованных одноименно; силовые линии показаны на рис. 3.

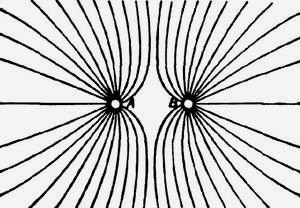
Рис. 3

Предположим, что А и В наэлектризованы положительно; так как силовые линии отходят от положительно наэлектризованного тела и оканчиваются на отрицательно наэлектризованном теле, то линии, отходящие от А и В, должны будут идти до какого-нибудь тела или тел, обладающих отрицательными зарядами, соответствующими положительным зарядам А и В. Предположим, что эти отрицательные заряды расположены на значительном расстоянии, так что силовые линии, исходящие из А, расположились бы равномерно по всем направлениям в рассматриваемой части поля, если бы не было заряда В.

Посмотрим теперь, что произойдет, если будем приближать друг к другу системы линий, связанных с А и В. Так как силовые линии отталкиваются друг от друга, то силовые линии с той стороны А, которая ближе к В, будут оттолкнуты на противоположную сторону А, так что теперь силовые линии будут сгущены на удаленной от В стороне А. Таким образом, притяжение А силовыми линиями сзади будет больше, чем спереди; в результате А будет отталкиваться от В. Мы видим, что механизм, вызывающий отталкивание, того же типа, что и механизм, вызывающий притяжение в предыдущем случае, и, если угодно, мы можем рассматривать отталкивание между А и В, как следствие притяжения их дополнительными отрицательными зарядами, которые должны существовать в других частях поля.

Результаты отталкивания силовых линий ясно показаны на рис. 4, изображающем случай двух противоположно наэлектризованных пластинок. Вы замечаете, что силовые линии между пластинками суть прямые, за исключением тех, которые находятся у краев пластинок. Этого как раз мы и должны были ожидать, так как в этой части поля давление сверху вниз, производимое силовыми линиями, находящимися над какой-либо линией, равно давлению снизу вверх силовых линий, находящихся под ней. Однако, для силовой линии, находящейся недалеко от края пластинки, давление внутренних силовых линий превосходит давление наружных, и силовая линий начнет изгибаться до тех пор, пока ее кривизна и натяжение не уравновесятся давлением изнутри; это искривление ясно показано на рис. 4.

До сих пор мы пользовались силовыми линиями скорее как средством для описания, чем средством для вычислений; между тем, развить теорию настолько, чтобы сделать ее аппаратом для вычислений, не так трудно. Мы можем это сделать, введя понятие о силовых трубках. Если мы проведем силовые линии через все точки контура маленькой замкнутой кривой, находящейся в электрическом поле, эти линии образуют трубчатую поверхность, и если мы продолжим эти линии назад до положительно заряженной поверхности, из которой они исходят, и вперед до отрицательно заряженной поверхности, на которой они оканчиваются, мы можем доказать, что положительный заряд, находящийся в начале трубки, равен отрицательному заряду, находящемуся в конце трубки. Выбирая подходящим образом площадь малой кривой, через которую мы проводим силовые линии, мы можем сделать заряд, заключенный в трубке, равным единице заряда. Назовем такую трубку фарадеевской трубкой, тогда каждая единица положительного электричества в этом поле может быть рассматриваема, как начало, а каждая единица отрицательного электричества, как конец фарадеевской трубки.

Мы приписываем фарадеевским трубкам направление; это направление совпадает с направлением электрической силы, так что положительное направление есть направление от положительного к отрицательному концу трубки. Если мы проведем в силовом поле замкнутую поверхность, то разность между числом фарадеевских трубок, выходящих из поверхности и входящих в нее, будет равна алгебраической сумме зарядов внутри поверхности; эту сумму Максвелл назвал электрическим смещением сквозь поверхность. То, что Максвелл назвал электрическим смещением в точке по какому-либо направлению, есть число фарадеевских трубок, которые проходят сквозь единицу площади, проведенной под прямым углом к этому направлению, причем число это считается алгебраическим, т.е. трубки, проходящие в одном направлении, считаются положительными, а в противоположном направлении — отрицательными, и число трубок, проходящих сквозь площадку, есть разность между числом трубок положительных и отрицательных.

С своей стороны, я нахожу, что понятие о фарадеевских трубках больше помогает нам представить себе мысленно картину процессов, происходящих в электрическом поле, чем понятие об электрическом смещении, поэтому уже много лет, как я оставил последний метод.

Максвелл остановился на вопросе о натяжении и давлении силовых линий в электрическом поле и продвинул эту проблему на шаг дальше, чем Фарадей. Подсчитывая величину этих натяжений, он показал, что механические действия в электрическом поле могут быть объяснены, если предположить, что каждая фарадеевская трубка испытывает натяжение, равное R, где R есть напряжение электрической силы, и что, кроме этого натяжения, в среде, сквозь которую проходят трубки, существует гидростатическое давление, равное NR/2, где N есть густота фарадеевских трубок, т.е. число трубок, проходящих сквозь единицу площади, пересекающую под прямым углом направление электрических сил.

Если мы рассмотрим действие этих натяжений и давления на единицу объема среды, находящейся в электрическом поле, мы увидим, что оно эквивалентно натяжению NR/2 вдоль направления электрической силы и такой же величины давлению по всем направлениям, перпендикулярным к этой силе.

Движение фарадеевских трубок

До сих пор мы предполагали, что фарадеевские трубки находятся в покое; перейдем теперь к изучению явлений, вызываемых движением этих трубок. Начнем с рассмотрения самого простого случая — двух параллельных пластинок А и В, из которых одна заряжена положительным, другая отрицательным электричеством. Предположим, что после заряжения пластинки соединяются проволочным проводником EFG (рис. 5). Этот проводник пройдет через некоторые внешние трубки; находясь внутри проводника, трубки сокращаются до молекулярных размеров и потому исчезнет то отталкивание, которое они оказывали на соседние трубки. Рассмотрим влияние этого обстоятельства на трубку PQ, находящуюся между пластинками. Первоначально PQ была в равновесии под влиянием собственного натяжения к отталкивания, производимого соседними трубками. Но отталкивание, которое производили трубки, перерезанные EFG, теперь исчезло, поэтому PQ не будет больше в равновесии, но будет толкаться по направлению к EFG. Итак, все больше и больше трубок будет вгоняться в EFG, и вся система трубок, находящихся между пластинками, продвинется по направлению к EFQ. Таким образом, пока происходит разряд пластинок, трубки, находящиеся между ними, движутся перпендикулярно к самим себе.

Какое физическое явление сопровождает это движение трубок? В результате соединения пластинок проводником EFG является электрический ток, текущий от положительно заряженной пластинки через EFG к отрицательно заряженной пластинке. Как известно, это сопровождается появлением магнитной силы между пластинками. Эта магнитная сила перпендикулярна к плоскости рисунка и равна силе тока в пластинке, умноженной на 4π; или, если σ есть плотность электрического заряда на пластинках, a v — скорость, с которой движется заряд, магнитная сила равна 4πσv.

[Tомсон делает предположение, что каждая фарадеевская трубка дает начало магнитному полю, напряжение которого M = 4πv где v — скорость движения трубки, причем направление M должно быть перпендикулярно к направлению трубки и направлению ее скорости. В данном случае, если число трубок на единицу площади будет σ, т.е. плотность заряда σ, то для напряжения магнитного поля имеем M = 4πσ. Если трубки движутся по направлению, образующему угол θ с их собственным направлением, то M = 4πσv sin θ. Подробнее об этом см. примечание IV. (Прим. ред.)]

Здесь мы наблюдаем два явления, которые не имеют места в постоянном электростатическом поле: одно — движение фарадеевских трубок, другое — существование магнитной силы. Это внушает мысль, что существует связь между этими двумя явлениями и что движение фарадеевских трубок сопровождается появлением магнитной силы. Я развил следствия из этого предположения и показал, что если между магнитной силой и движением трубок существует именно та зависимость, которая указана дальше, то эта точка зрения может объяснить законы Ампера, касающиеся связи между током и магнитной силой, и законы Фарадея об индукции токов. Великий вклад Максвелла в теорию электричества, именно положение его, что изменение электрического смещения в диэлектрике вызывает магнитную силу, непосредственно следует из этой точки зрения [см. примечание IV]. Действительно, если электрическое смещение измеряется густотой фарадеевских трубок, то при изменении электрического смещения в каком-нибудь месте фарадеевские трубки должны двигаться к этому месту или от него, а движение фарадеевских трубок, согласно гипотезе, вызывает магнитную силу.

Закон, связывающий магнитную силу с движением фарадеевских трубок, следующий: фарадеевская трубка в точке Р, движущаяся со скоростью v, вызывает в Р магнитную силу, равную 4πvsinθ, причем направление магнитной силы перпендикулярно к фарадеевской трубке и к направлению движения; θ есть угол между фарадеевской трубкой и направлением ее движения. Мы видим, что только движение трубки, направленное под прямым углом к ней самой, производит магнитную силу; такая сила не возникает при скольжении трубки вдоль ее длины.

Движение заряженной сферы

Приложим эти результаты к очень простому, но важному случаю равномерного движения заряженной сферы. Если скорость сферы мала сравнительно со скоростью света, то фарадеевские трубки будут равномерно распределены по радиальным направлениям, как если бы сфера была в покое. Они будут перемещаться вместе со сферой. Если е есть заряд на сфере, О — ее центр, то густота фарадеевских трубок в точке Р будет e/4πОР²; поэтому, если v есть скорость сферы, θ —угол между ОР и направлением движения сферы, то, согласно вышенаписанному закону, магнитная сила в Р будет evsinθ/r², направление силы будет перпендикулярно к ОР и к направлению движения сферы. Линии магнитной силы окажутся окружностями, центры которых лежат на траектории центра сферы, а их плоскости перпендикулярны к той же траектории. Таким образом, движущийся заряд электричества сопровождается магнитным полем. Существование магнитного поля предполагает наличность энергии; мы знаем, что в единице объема поля, где магнитная сила Н, заключает μH²/8π единиц энергии, причем μ есть магнитная проницаемость среды. В случае движения сферы энергия на единицу объема в Р будет равна μ(evsinθ)²/8πОР⁴. Суммируя энергию для всех частей поля, кроме сферы, мы находим, что она равна μ(ev)²/3a, где а — радиус сферы.

Если m есть масса сферы, то кинетическая энергия сферы есть mv²/2; к ней надо добавить энергию вне сферы, которая равна, как мы видели, μ(ev)²/3a; поэтому полная кинетическая энергия системы равна m'v²/2, где m' = m + 2μe²/3a. Итак, вследствие электрического заряда масса сферы увеличилась на 2μe²/3a. Это очень важный результат, так как он показывает, что часть массы заряженной сферы обязана своим происхождением ее заряду. Позже я предложу вам соображения, которые показывают возможность того, что вся масса тела имеет такое же происхождение.

Однако, прежде чем перейти к этому пункту, я хотел бы иллюстрировать это увеличение массы сферы некоторыми аналогиями из других отделов физики, Первая из них есть случай сферы, движущейся в жидкости без трения. Когда сфера движется, она заставляет двигаться окружающую жидкость со скоростью, пропорциональной собственной скорости, так что, двигая сферу, мы должны приводить в движение не только вещество самой сферы, но и окружающую жидкость. В результате сфера ведет себя так, как будто ее масса увеличилась на некоторый определенный объем жидкости. Этот объем, как было показано Грином в 1833 г., равен половине объема сферы. В случае цилиндра, движущегося перпендикулярно к своей длине, масса его увеличивается на массу равного ему объема жидкости. В случае удлиненного тела, в роде цилиндра, величина, на которую возрастает масса, зависит от направлении движения тела, делаясь наименьшим, когда тело движется концами вперед, чем при движении боком. Масса такого тела зависит от направления, в котором оно движется.

Возвратимся, однако, к движению наэлектризованное сферы. Мы видели, что благодаря заряду ее масса увеличилась на 2μe²/3a; поэтому если она движется со скоростью v, количество движения будет не mv, но m'v, где m' равно m + 2μe²/3a. Добавочное количество движения находится не в сфере, а в пространстве, окружающем сферу. Пространство будет иметь обыкновенное механическое количество движения, результирующая которого есть 2μev²/3a и направление которого параллельно направлению движения сферы.

Важно помнить, что это количество движения ни в каком отношении не отличается от обычного механического количества движения и может быть прибавлено или отнято от количества движения движущихся тел. Я хотел бы представить перед вами существование этого количества движения насколько возможно ярко и убедительно, потому что после признания этого факта состояние электрического поля делается вполне аналогичным состоянию механической системы. Например, по третьему закону Ньютона действие и противодействие равны и противоположны, так что в изолированной системе количество движения в каком-либо направлении неизменно. Но во многих электрических системах как будто нарушается этот принцип, напр., в случае покоящегося заряженного тела, на которое действует электрический импульс; заряженное тело под влиянием электрической силы этого импульса приобретает скорость и количество движения, так что количество движения после прохождения импульса уже не то, что в начале.

Таким образом, если мы сосредоточили наше внимание только на количестве движения заряженного тела, т.е., если мы предположим, что количество движения обязательно ограничивается тем, что мы рассматриваем как обыкновенную материю, то будем иметь отступление от третьего закона движения, потому что количество движения, рассматриваемое с этой узкой точки зрения, изменилось. Однако явление это находятся в полном согласии с законом, если признать существование количества движения в электрическом поле, потому что, с этой точки зрения, прежде чем импульс достиг заряженного тела, количество движения было сосредоточено в электрическом импульсе, а не в теле; после того как импульс коснулся тела, в последнем появилось некоторое количество движения, в импульсе же оно уменьшилось так, что количество движения, приобретенное телом, как раз равняется количеству движении, потерянному импульсом.

Перейдем теперь к более подробному рассмотрению количества движения, В своих "Новых исследованиях по электричеству и магнетизму" [первая часть первой главы этой книги приведена в настоящем издании, см. приложение IV] я подсчитал величину количества движения для любой точки электрического поля и показал, что, если N есть число фарадеевских трубок, проходящих сквозь единицу поверхности, перпендикулярной к их направлению, В — магнитная индукция, θ — угол между индукцией и фарадеевскими трубками, то количество движения, приходящееся на единицу объема, равно NBsinθ, направление же его перпендикулярно к магнитной индукции и фарадеевским трубкам [см. приложение IV]. Многие из вас заметят, что количество движения параллельно так называемому вектору Пойнтинга, направление которого совпадает с направлением распространения энергий в поле.

Момент количества движения, произведенный наэлектризованной точкой и магнитным полюсом

Чтобы освоиться с распределением количества движения, рассмотрим детально несколько простых случаев. Начнем с простейшего, соответствующего наэлектризованной точке и магнитному полюсу. Пусть А (рис. 7) будет точкой, а В — полюсом. Так как количество движения в какой-нибудь точке Р перпендикулярно к АР — направлению фарадеевских трубок и к ВР — магнитной индукции, то количество движения будет перпендикулярно к плоскости AВP. Таким образом, если проведем серию линий, направление которых в каждой точке совладает с направлением количества движения в той же точке, то эти линии образуют серию окружностей, плоскости которых перпендикулярны к прямой АВ, а центры лежат на этой же прямой. Это распределение количества движения, поскольку дело идет о направлении, будет то самое, каким обладает волчок, вращающийся вокруг оси АВ. Найдем теперь, чему эквивалентно такое распределение количества движения по всему полю.

Очевидно, что результирующее количество движения в каком-либо направлении равно нулю, но так как система вращается вокруг оси АВ и направление вращения везде одно и то же, то должен существовать конечный момент количества движения относительно оси АВ. Подсчитывая его величину на основании выражения, данного выше для количества движения, мы получим для величины момента количества движения относительно оси АВ очень простое выражение, а именно: em, где е есть заряд точки, a m — магнитная масса полюса. При помощи этого выражения мы можем сразу определить момент количества движения для любого распределения наэлектризованных точек и магнитных полюсов.

Вернемся снова к системе точки и полюса. Понятие о количестве движения системы приводит нас непосредственно к определению силы, действующей на движущийся электрический заряд или движущийся магнитный полюс. Для этого предположим, что за время δt на электризованная точка переместится из А в А', момент количества движения будет по-прежнему em, но осью его будет А'В вместо АВ (рис. 8). Итак, момент количества движения поля изменился, но результирующий момент количества движения всей системы, охватывающей точку, полюс к поле, должен оставаться постоянным; поэтому изменение момента количества движения поля должно компенсироваться равным и противоположным изменением момента количества движения полюса и точки. Количество движения, приобретенное точкою, должно быть равно и противоположно количеству движения, приобретенному полюсом, так как полное количество движения равно нулю.

Если θ есть угол АВА', изменение момента количества движения будет emsinθ с осью, перпендикулярной к АВ и лежащей в плоскости рисунка. Пусть δJ будет изменение количества движения в А, а — δJ изменение в В, тогда δJ и – δJ должны быть эквивалентны такой паре, ось которой лежит в плоскости рисунка и перпендикулярна к АВ, а момент равен emsinθ. Таким образом, δJ должно быть перпендикулярно к плоскости рисунка и

ABδJ = emsinθ = АА'emsinφ/AB, где φ = BАА'.

Если v — скорость точки А, АА' = vδt, то мы получим:

δJ = emvsinφδt/AB².

Изменение количества движения может быть рассматриваемо, как результат действия силы F, перпендикулярной к плоскости рисунка и равной скорости возрастания количества движения, или δJ/δt. Мы получим, таким образом, F = emvsinφ/AB, т.е. точка А испытывает действие силы, равной e умноженному на составляющую магнитной силы по направлению, перпендикулярному к направлению движения. Направление силы, действующей на точку, перпендикулярно к ее скорости и к магнитной силе. На магнитный полюс действует равная и противоположная сила.

Значение, которое мы нашли для F, есть обычное выражение для механической силы, действующей на заряженную частицу, движущуюся в магнитном поле. Оно может быть записано так: evНsinφ, где Н есть напряжение магнитного поля. Поэтому сила, действующая на единицу заряда, есть vНsinφ. Таким образом, эту механическую силу можно считать происходящей от электрической силы vНsinφ, и мы можем выразить результат, говоря, что, когда заряженное тело движется в магнитном поле, возникает электрическая сила vНsinφ. Эта сапа есть хорошо известная электродвижущая сила индукции, вызванная движением в магнитном поле.

Силы, о которых здесь идет речь, вызываются относительным движением точки и поля. Если последние движутся с одной и той же скоростью, линия, их соединяющая, не изменит своего направления, момент количества движения системы останется неизменным, и поэтому не будет сил, действующих ни на точку ни на полюс.

Распределение количества движения в системе, состоящей из полюса и точки, подобно в некоторых отношениях распределению количества движения в волчке, вращающемся вокруг прямой АВ. Мы можем иллюстрировать силы, действующие на движущееся наэлектризованное тело, при помощи такого волчка. Рис. 9 представляет уравновешенный гироскоп, вращающийся вокруг оси АВ. Пусть груз в точке А изображает наэлектризованную точку, а груз в точке В — магнитный полюс. Предположим, что гироскоп вращается, когда ось АВ горизонтальна. Тогда, если я вертикально расположенной палочкой буду толкать АВ в горизонтальном направлении, точка А будет двигаться не только горизонтально вперед в том направлении, в каком ее толкают, но будет двигаться вертикально вверх или вниз, совершенно так же, как это делала бы заряженная точка, толкаемая вперед в том же направлении и находящаяся под воздействием магнитного полюса в точке В.

Рис. 9


Вектор-потенциал Максвелла

Существует очень тесная связь между количеством движения, происходящим от наэлектризованной точки и магнитной системы, и вектором-потенциалом этой системы, величиной, играющей большую роль в максвелловской теории электричества. Из выражения, которое мы дали для момента количества движения, вызванного наэлектризованной точкой и магнитным полюсом, мы можем сразу найти момент количества движения, образованного зарядом электричества e в точке Р и маленьким магнитом АВ. Пусть отрицательный полюс магнита будет в точке А, положительный — в точке В, и пусть m — магнитная масса каждого полюса. Простое вычисление показывает, что в этом случае ось результирующего момента количества движения находится в плоскости РАВ и перпендикулярна к РО, где О — середина АВ, и что величина момента количества движения равна emABsinφ/OP, где φ — угол, образованный прямыми АВ и OP. Этот момент количества движения эквивалентен по направлению и величине моменту, вызванному количеством движения emABsinφ/OP² в точке P, направленным перпендикулярно к плоскости PАВ и равным по величине, но противоположным по направлению количествам движения в точке O. Вектор emABsinφ/OP² в точке P, перпендикулярный к плоскости PАВ, есть вектор, названный Максвеллом вектором-потенциалом в точке Р, образованным магнитом.

Обозначая этот вектор-потенциал через J, мы видим, что количество движения, вызванное зарядом и магнитом, эквивалентно количеству движения eJ в точке Р и количеству движения – eJ в магните.

Мы можем, очевидно, распространить найденный результат на любую сложную систему магнитов, так что если J есть вектор-потенциал в точке Р то количество движения во всем поле эквивалентно количеству движения еJ в точке Р вместе с количеством движения каждого магнита, равным –е, умноженным на вектор-потенциал в точке Р, вызванный этим магнитом. Если магнитное поле образовано только электрическими токами вместо постоянных магнитов, количество движения системы, состоящей из одной наэлектризованной точки и токов, будет в некоторых отношениях отличаться от количества движения для случая, когда магнитное поле образовано постоянными магнитами. В последнем случае, как мы видели, имеется момент количества движения, но нет результирующего количества движения. Если же, однако, магнитное поле создано только электрическими токами, то легко показать, что существует результирующее количество движения, но момент количества движения относительно какой-нибудь прямой, проходящей через наэлектризованную точку, исчезает. Простой подсчет показывает, что полное количество движения, в поле эквивалентно количеству движения еJ в наэлектризованной точке, причем J — вектор-потенциал, созданный токами в точке Р.

Итак, будет ли магнитное поле создано постоянными магнитами, или электрическими токами или частично тем, частично другим, — все равно количество движения, если наэлектризованная точка помещена в точку Р поля, эквивалентно количеству движения еJ в точке Р где J есть вектор-потенциал в точке Р. Если магнитное поле образовано только токами, это есть полное выражение количества движения в поле; если же магнитное поле отчасти создано магнитами, то к количеству движения в Р надо добавить другие количества движения в магнитах; величина количества движения в каждом отдельном магните есть –е, умноженное на вектор-потенциал в точке Р, созданный этим магнитом.

Хорошо известные выражения электродвижущей силы электромагнитной индукции сразу получаются из этого результата. На основании третьего закона движения, количество движения всякой замкнутой системы должно оставаться постоянным. Количество движения состоит из: (1) количества движения в поле, (2) количества движения наэлектризованной точки и (3) количества движения магнитов или токов.

Так как (1) эквивалентно количеству движения еJ в наэлектризованной частице, мы видим, что изменения количества движения поля должны компенсироваться изменениями количества движения частицы. Пусть М — масса наэлектризованной частицы, u, v, w — составляющие ее скорости, параллельные осям x, y, z; F, G, H — составляющие вектора-потенциала в точке P, параллельные тем же осям; тогда количество движения поля эквивалентно количествам движения еF, еG, еH в точке P, параллельным осям x, y, z, а количество движения заряженной частицы в точке P имеет своими составляющими Мu, Мv, Мw. Так как количество движения остается постоянным, Мu + eF тоже постоянно; поэтому, если δu и δF — одновременные изменения u и F, то Мδu + еδF = 0 или М (du/dt) = –е (dF/dt).

Из этого уравнения мы видим, что заряженная точка ведет себя так, как если бы она подвергалась действию механической силы, параллельной оси x и равной –е (dF/dt), т.е. электрической силы, равной –dF/dt. Тем же путем мы убедимся, что существуют электрические силы –dG/dt и –dH/dt, соответственно параллельные осям y и z. Это есть хорошо известные силы, созданные электромагнитной индукцией, и мы видим, что они представляют прямое следствие принципа: действие и противодействие равны и противоположны.

Читатели "Экспериментальных исследований" Фарадея припомнят, что он постоянно ссылается на то, что было им названо электротоническим состоянием. Так, он смотрит на проволоку, по которой идет ток, как на находящуюся в электротоническом состоянии, если она помещена в магнитном попе. Никаких следов этого состояния нельзя открыть, пока поле остается постоянным; оно обнаруживается только при изменениях поля. Это электротоничешое состояние Фарадея и есть как раз количество движения, существующее в поле.

Глава II. Электрическая и связанная масса

В этой главе я хочу рассмотреть связь между количеством движения в электрическом поле и фарадеевскими трубками, посредством которых, как я сказал в последней лекции, мы можем представить себе состояние такого поля.

Рассмотрим сначала случай заряженной сферы, находящейся в движении.

Рис. 10

Линии электрической силы направлены по радиусам; линии магнитной силы будут окружностями, для которых линия движения центра сферы будет служить общей осью, количество движения в точке Р перпендикулярно к этим направлениям и, таким образом, перпендикулярно к ОР и лежит в плоскости, содержащей точку Р и траекторию центра сферы. Если N есть число фарадеевских трубок, проходящих через единицу площади в Р, проведенной перпендикулярно к ОР, μ — магнитная проницаемость среды, окружающей сферу, то магнитная индукция в Р будет 4πμvN sinθ, v — скорость движения сферы. Количество движения в единице объема среды в Р равно 4πμvN² sinθ и имеем направление составляющей скорости фарадеевской трубки, перпендикулярной к их длине. Это есть в точности то количество движения, которое появилось бы, если бы трубки, двигаясь под прямым углом к своей длине, увлекали с собой из окружающей среды массу, равную 4πμN² на единицу объема, причем сами трубки совсем бы не обладали массой и не увлекали бы с собой массы из среды, когда они скользят параллельно своей длине.

Предположим, в самом деле, что трубки ведут себя приблизительно так же, как длинные, узкие цилиндры, движущиеся в воде; последние, двигаясь концами вперед, т. е. параллельно своей длине, увлекают очень малое количество воды, тогда как при боковом движении, т. е. перпендикулярно оси, каждая единица длины трубки увлекает с собою некоторую конечную массу воды. Когда длина цилиндра очень велика сравнительно с его шириной, то можно массой воды, увлекаемой им при движении концом вперед, пренебречь в сравнении с той, которая увлекается им при движении в сторону. Если трубка не имеет другой массы, кроме той, которую она получает вследствие смещения воды, то она будет иметь массу только при движении в сторону но не при движении концом вперед.

Назовем массу 4πμN², увлекаемую трубками в единице объема, массой связанного эфира. Следует отметить тот факт, что электростатическая энергия Е в единице объема пропорциональна М — массе связанного эфира в этом объеме. Это может быть легко доказано следующим образом: Е = 2πN²/К, К — диэлектрическая постоянная среды. Так как М = 4πμN², то Е = М/2μК. Но V² = 1/μК, где V — скорость распространения света в рассматриваемой среде. Поэтому Е = МV²/2. Таким образом, Е равно кинетической энергии, которою обладает связанная масса, движущаяся со скоростью света.

Масса связанного эфира в единице объема равна 4πμN², где N — число фарадеевских трубок, поэтому величина связанной массы, приходящейся на единицу длины каждой фарадеевской трубки, равна 4πμN. Мы видели, что эта величина пропорциональна напряжению в каждой трубке, так что можем рассматривать фарадеевские трубки, как туго натянутые волокна с переменными массами и натяжениями, причем натяжение везде пропорционально массе единицы длины волокна.

Так как масса эфира, захватываемого фарадеевской трубкой, пропорциональна N, числу фарадеевских трубок в единице объема, то отсюда видно, что масса и количество движения фарадеевской трубки зависят не только от очертания и скорости рассматриваемой трубок, но и от числа и скорости соседних фарадеевских трубок. Мы имеем некоторые аналогии этому в динамических системах; напр., в случае движения в несжимаемой жидкости нескольких близко расположенных цилиндров с параллельными осями, количество движения какого-нибудь цилиндра зависит от положения и скоростей соседних цилиндров. Следующая гидродинамическая система может послужить для иллюстрации того факта, что связанная масса пропорциональна квадрату числа фарадеевских трубок в единице объема.

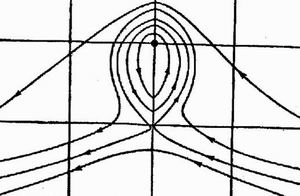
Рис. 11

Предположим, что у нас имеется цилиндрический вихревой столб силы m, помешенный в массу жидкости, скорость которой, если бы она не нарушалась вихревым столбом, оставалась бы постоянной по величине и направлению и перпендикулярной к оси вихревого столба. Линии потоков для этого случая представлены на рис. 11, где А есть сечение вихревого столба, ось которого предполагается перпендикулярной к плоскости рисунка. Мы видим, что некоторые из этих линий в соседстве со столбом представляют замкнутые кривые. Так как линии потоков в жидкости не пересекаются, то жидкость, заключенная внутри замкнутой кривой, будет всегда оставаться в соседстве со столбом и вместе с ним перемещаться. Таким образом, столб увлечет с собой массу жидкости, равную массе, находящейся в самой большой из замкнутых линий потоков. Если m будет сила вихревого столба, а — скорость ненарушаемого вихрем течения жидкости, то можно легко показать, что масса увлекаемой столбом жидкости пропорциональна m²/а². Таким образом, если будем считать m пропорциональным числу фарадеевских трубок в единице объема, эта система будет нам иллюстрировать связь, существующую между силой электрического поля и связанной массой.

Влияние скорости на связанную массу

Я рассмотрю теперь другое следствие, вытекающее из той идеи, что масса заряженной частицы обязана своим происхождением массе эфира, заключенного в фарадеевских трубках, связанных с зарядом. Когда эти трубки движутся нормально к своей длине, они увлекают с собой определенное количество эфира, сквозь который они движутся; когда же они перемещаются параллельно своей длине, они скользят сквозь эфир, не приводя его в движение. Рассмотрим теперь, как ведет себя схожий по форме с фарадеевской трубкой длинный и тонкий цилиндр, при движении в жидкости.

Такое тело, свободно поворачивающееся в любом направлении, не будет, как можно было бы ожидать с первого взгляда, перемещаться концом вперед, но наклоняется к направлению движения, причем наклоняется так, чтобы увлечь с собою насколько возможно больше той жидкости, сквозь которую движется. Можно было бы привести не одно явление, иллюстрирующее этот принцип; одно из наиболее доступных — падение листьев: они не падают на землю краем вперед, но плавно спускаются вниз, сохраняя свою плоскость более или менее горизонтальной.

Если применим этот принцип к заряженной сфере, то увидим, что фарадеевские трубки, связанные со сферою, стремятся расположиться перпендикулярно к направлению движения сферы, так что, если бы приходилось считаться только с этим принципом, то все фарадеевские трубки оказались бы сосредоточенными в экваториальной плоскости, т. е. плоскости, перпендикулярной к направлению движения сферы, так как при таком положении они все будут перемешаться перпендикулярно к своей длине. Мы должны, однако, вспомнить, что фарадеевские трубки взаимно отталкиваются, так что, если бы они все столпились в экваториальной плоскости, давление там было бы больше, чем у полюса. Это отбросит фарадеевские трубки назад в то положение, при котором они были равномерно распределены вокруг сферы. Действительное распределение фарадеевских трубок представляет компромисс между этими крайними случаями. Они не столпятся все в экваториальной плоскости и не распределятся равномерно, но в экваториальной области их будет больше, чем в других, при этом плотность их в экваториальной области возрастает вместе со скоростью движения заряда. Когда фарадеевская трубка расположена в экваториальной области, она захватывает с собою больше эфира чем тогда, когда она находится вблизи полюса; поэтому смещение фарадеевских трубок от полюса к экватору увеличивает общее количество увлекаемого трубками эфира, а следовательно, и массу тела.

Было доказано (см. Heaviside, Phil. Mag., April, 1889, "Recent Researches", стр. 19), что в результате движения сферы каждая фарадеевская трубка смещается по направлению к экваториальной плоскости, т. е. плоскости, проходящей через центр сферы и перпендикулярной к направлению движения. При этом смещение происходит таким образом, чтобы проекция трубки на эту плоскость оставалась такоавномерном распределении трубок, а расстояние каждой точки трубки от экваториальной плоскости уменьшалось в отношении (V² – v²)^½, где V — скорость распространения света в среде, a v — скорость движения заряженного тела.

Этот результат показывает, что только в том случае изменение в распределении фарадеевских трубок, вызванное движением тела, делается заметным, когда скорость заряженного тела сравнима со скоростью света.

В "Recent Researches on Electricity and Magnetism", стр. 21, я подсчитал количество движения J в пространстве, окружающем сферу радиуса a, центр которой находится на движущемся зараженном теле, и показал, что значение J дается следующим выражением:

    (*)

где, как и раньше v и V суть соответственно скорость частицы и скорость света, угол θ определяется из уравнения sinθ = v/V.

Масса сферы вследствие заряда возрастает на J/v, и, таким образом, как показывает уравнение (*), для скоростей заряженного тела, сравнимых со скоростью света, масса тела возрастает вместе со скоростью.

Из уравнения (*) очевидно, что для того, чтобы обнаружить влияние скорости на массу, мы должны воспользоваться чрезвычайно маленькими частицами, движущимися с очень большими скоростями. Частицы, имеющие массу значительно меньшую, чем масса какого-либо известного нам атома или молекулы, вылетают из радия со скоростями, приближающимися в некоторых случаях к скорости света; отношение электрического заряда к массе для частиц такого рода было недавно предметом исследования Кауфманна, результаты которого приведены в следующей таблице (I). В первом столбце находятся значения скоростей частицы, выраженные в сантиметрах в секунду, второй столбец содержит значения дроби — e/m где e — заряд, а m — масса частицы.

Таблица I

v · 10 –10	(e/m) · 10 –7
2,85	0,62
2,72	0,77
2,59	0,975
2,48	1,17
2,36	1,31

Эти цифры показывают, что значение e/m уменьшается с возрастанием скорости; если предположим, что заряд остается неизменным, то это означает, что масса возрастает вместе со скоростью. Результаты опытов Кауфманна дают нам возможность сравнить ту часть массы, которая обусловлена электрическим зарядом, с тою частью, которая не зависит от электризации; эта вторая часть массы не зависит от скорости. Если мы находим, что масса заметно изменяется со скоростью, мы заключаем, что часть массы, обязанная своим происхождением заряду, должна быть значительной по сравнению с той, которая не зависит от заряда. Чтобы подсчитать влияние скорости на массу электрической системы, мы должны сделать некоторые предположения относительно природы этой системы, так как влияние на заряженную сферу, например, не то же самое, что на заряженный эллипсоид; но, сделав эти предположения и вычислив теоретически влияние скорости на массу, легко найти отношение той части массы, которая не зависит от заряда, к той части, которая при некоторой скорости, зависит от заряда.

Положим, что часть массы, созданная электризацией, при скорости v равна m₀ f(v), где f(v) есть известная функция v; тогда если M_v и M_v' представляют наблюденные массы соответственно при скоростях v и v', а M есть часть массы, не зависящая от заряда, получим два уравнения: M_v = M + m₀ f(v) и M_v' = M + m₀ f(v'), из которых можно определить M и m₀ . Сделав предположение, что заряженное тело ведет себя как металлическая сфера, для которой распределение силовых линий при движении было определено Сирлом (G. R С. Searle), Кауфманн пришел к заключению, что когда частица медленно движется, ее "электрическая масса" составляет приблизительно четвертую часть всей массы. Он настоятельно указывает, что эта дробь зависит от тех предположений, которые мы делаем относительно природы движущегося тела, например, будет ли оно сферическим или эллипсоидальным, изолятором или проводником, и что при других предположениях его опыты могли бы показать, что вся масса — электрическая, что он, очевидно, считал наиболее вероятным.

При современном состоянии наших знаний о строении материи, я не думаю, чтобы мы что-нибудь выиграли, приписывая маленьким, отрицательно заряженным частицам, выделяемым радием и другими телами, свойства металлической проводимости. Я предпочитаю более простое предположение что распределение силовых линий вокруг частицы то же самое, как у силовых линий заряженной точки, если только мы ограничим наше внимание полем, окружающим малую сферу радиуса а, имеющую центр в заряженной точке. При таком предположении часть массы, созданная зарядом, равна значению — J/v в уравнении (*).

Я подсчитал из этого выражения отношение масс быстро движущихся частичек, испускаемых радием, к массе тех же частичек, пребывающих в покое или медленно движущихся, при том предположении, что вся масса создана зарядом и сравнил эти результаты со значениями того же отношения, определенными на основании опытов Кауфманна. Эти результаты приведены в следующей таблице (II), первый столбец которой содержит значение v, скорости частиц; второй — р — число, показывающее на основании уравнения (*), во сколько раз масса частицы, движущейся с этой скоростью, превосходит массу той же частицы, находящейся в покое; третий столбец — р' — значения той же величины, найденные Кауфманном из его опытов.

Таблица II

v · 10 –10	p	p'
2,85	3,1	3,09
2,72	2,42	2,43
2,59	2,0	2,04
2,48	1,66	1,83
2,36	1,5	1,65

Эти результаты подтверждают тот взгляд, что вся масса наэлектризованных частичек происходит от их заряда.

Мы уже видели, что если рассматривать фарадеевские трубки, связанные с этими движущимися частицами, как обусловленные движущейся заряженной точкой, и ограничить свое внимание той частью поля, которая находится вне сферы радиуса а, концентричной с зарядом, то в случае медленного движения частицы масса m, обусловленная зарядом е на частице, определяется из уравнения: 2μe²/3a.

В одной из следующих лекций я объясню, как определяются значения mе и е; результаты этих определений таковы: m/е = 10 ^–7 и е = 1,2 · 10 ^–20 CGS электростатических единицах. Подставляя эти значения в выражение для m, мы находим, что а равно приблизительно 5 · 10 ^–14 см, длина очень маленькая в сравнении с величиной 10 ^–8 см, которая обыкновенно берется, как хорошее приближение к размеру молекулы.

Мы рассматривали массу в данном случае как массу эфира, увлекаемого фарадеевскими трубками, связанными с зарядом. Так как трубки простираются на бесконечное расстояние, масса частицы как бы рассеяна во всем пространстве и не имеет определенных границ. Однако, благодаря тому, что частица имеет очень малые размеры, а масса эфира, увлекаемого трубками, будучи пропорциональна квадрату плотности фарадеевских трубок, изменяется обратно пропорционально четвертой степени расстояния от частицы, мы простым вычислением находим, что вся масса, за исключением очень незначительной части, находится на конечном расстоянии от частицы, которое в действительности очень мало сравнительно с теми размерами, которые обычно приписывают атомам.

В любой системе, содержащей наэлектризованные тела, часть массы состоят из массы эфира, увлекаемого фарадеевскими трубками, связанными с электризацией. Согласно одному из взглядов на строение материи, который я надеюсь развить в одной из последующих лекций, атомы различных элементов представляют совокупности положительных и отрицательных зарядов, удерживающихся вместе, главным образом, электрическими притяжениями. Кроме того, отрицательно заряженные частицы в атоме (я назвал их корпускулами) идентичны с теми маленькими отрицательно заряженными частицами, свойства которых мы исследовали. С этой точки зрения на строение материи, часть массы какого-нибудь тела представляет собою массу эфира, увлекаемого фарадеевскши трубками, пронизывающими атом между его положительными и отрицательными элементами.

Взгляд, который я хочу перед вами развить, состоит в том, что не только часть массы какого-либо тела происходит таким путем, но что вся масса любого тела есть как раз масса эфира, окружающего тело и увлекаемого фарадеевскими трубками, связанными с атомами тела. Одним словом, вся масса есть масса эфира, всякое количество движения есть количество движения эфира, всякая кинетическая энергия есть кинетическая энергия эфира. Надо сказать, что этот взгляд требует, чтобы плотность эфира была неизмеримо больше, чем плотность любого известного нам вещества.

Можно возразить, что, так как масса увлекается фарадеевскими трубками и так как расположение последних зависит от относительного положения наэлектризованных тел, то масса какой-нибудь совокупности положительно и отрицательно наэлектризованных тел постоянно менялась бы с положением этих тел и, таким образом, вместо того, чтобы быть, как показывают наблюдения и опыты, постоянной с очень высокой степенью приближения, масса должна была бы меняться вместе с изменениями в физическом и химическом состоянии тела.

Однако, эти возражения не применимы к такому случаю, который рассматривался вышеизложенной теорией, где размеры одной группы наэлектризованных тел — отрицательных — чрезвычайно малы сравнительно с расстояниями, разделяющими различные члены системы наэлектризованных тел. В этом случае концентрация силовых лиши на маленьких отрицательных телах — корпускулах — так велика, что практически весь связанный эфир расположен, вокруг этих тел, и количество его зависит от их объема и заряда. Таким образом, если мы только не меняем числа или характера корпускул, изменения массы, происходящие вследствие какого-либо изменения в их относительном положении, будут совершенно незначительны в сравнении с массою тела.

Глава III. Результаты ускорения фарадеевских трубок

Лучи рентгена и свет

Мы рассмотрели, как ведут себя силовые линии, когда они находятся в покое или в равномерном движении; в этой главе мы рассмотрим те явления, которые получаются в результате неравномерного движения.

Начнем со случая движущейся заряженной точки, движущейся так медленно, что силовые линии вокруг нее распределены равномерно, и посмотрим, что должно случиться, если мы внезапно остановим точку. Фарадеевские трубки, соединенные со сферой, обладают инерцией. Они находятся также в состоянии натяжения, причем натяжение в какой-либо точке пропорционально массе единицы длины. Поэтому любое возмущение, сообщенное одному концу трубки, пройдет вдоль нее с постоянной и конечной скоростью. Действительно, фарадеевская трубка представляет замечательную аналогию с натянутой струной.

Положим, что имеем туго натянутую вертикальную струну, движущуюся равномерно справа налево. Когда мы внезапно остановим этот конец, напр., в А, что случится со струной? Конец А сразу придет в состояние покоя, но силы, при этом обнаруживающиеся, распространяются с конечной скоростью, и каждая часть струны будет по инерции двигаться, как будто ничего не случилось с концом А, до тех пор, пока возмущение, выходящее из точки А, не достигнет ее. Итак, если V есть скорость, с которой возмущение перемещается вдоль струны, a t есть время, которое протекло после остановки А, то части струны, находящиеся от А на расстояниях больших, чем Vt, не почувствуют остановки и будут иметь те же скорости и положения, какие они имели бы, если бы струна продолжала равномерно двигаться вперед. Форма струны через последовательные промежутки времени показана на рис. 12. Длина горизонтальный части убывает по мере увеличения расстояния от неподвижного конца.

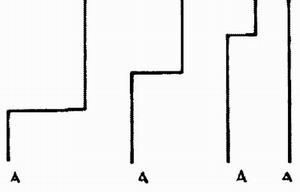
Рис. 12

Возвратимся теперь к тому случаю, когда движущаяся заряженная частица внезапно останавливается, причем на остановку тратится время τ. Чтобы найти конфигурацию фарадеевских трубок после того, как от начала процесса остановки заряженной частицы прошло время t, опишем из заряженной частицы, как из центра, две сферы, одну радиусом Vt, другую — радиусом V(t – τ); так как возмущение еще не достигло тех частей фарадеевских трубок, которые расположены вне нашей внешней сферы, то эти трубки будут в том же положении, в каком они находились бы, если бы продолжали двигаться вперед с той скоростью, какой они обладали в момент остановки частицы, между тем как трубки, находящиеся внутри внутренней сферы, займут свое конечное положение, так как возмущение уже прошло через них.

Так, рассмотрим трубку, которая была расположена вдоль линии OPQ (рис. 13), когда частица остановилась. Это будет конечным положением трубки, так как в момент t часть трубки в пространстве внутренней сферы займет положение ОР, между тем как часть P'Q' вне внешней сферы будет в том положении, какое она занимала бы, если бы частица не остановилась, т.е. если О' есть положение, которое занимала бы частица, если бы она не остановилась. P'Q' будет прямой линией, проходящей через О'. Чтобы сохранить свою непрерывность, трубка должна изогнуться в промежутке между обеими сферами и примет поэтому форму OPP'Q'.

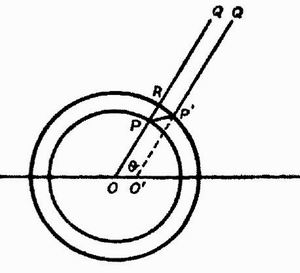
Рис. 13

Таким образом, трубка, которая до остановки частицы была радиальной, имеет теперь в промежутке между сферами тангенциальную составляющую, обусловливающую тангенциальную электрическую силу. Остановка частицы вызывает радикальное изменение в электрическом поле, созданном частицей и, как показывает нижеследующее вычисление, вызывает электрические и магнитные силы более значительные чем те, которые существуют в поле, когда частица движется равномерно.

Если мы предположим, что толщина δ промежутка так мала, что часть фарадеевской трубки внутри его может быть рассматриваема, как прямая, тогда, если Т есть тангенциальная электрическая сила внутри волнового импульса, R — радиальная сила, будем иметь: Т/R = P'R/PR = OО'sinθ/δ = vtsinθ/δ.

Здесь v есть скорость, с которой частица движется до остановки, θ — угол который ОР образует с направлением движений частицы, t — время, протекшее после остановки частицы; так как R = e/OP² и ОР = Vt, где V — скорость света, получим Т = evsinθ/Vrδ, если r = ОР.

Тангенциальная фарадеевская трубка, движущаяся вперед со скоростью V, вызывает в Р магнитную силу Н, равную VТ. Эта сила будет перпендикулярна к плоскости чертежа и будет по направлению противоположна магнитной силе, существовавшей в Р до остановки частицы. Так как ее величина определяется уравнением Н = evsinθ/rδ, то она превосходит магнитную силу eVsinθ/r², ранее существовавшую, в отношении r к δ.

Таким образом, волновой импульс, вызванный остановкой частицы, есть место действия интенсивных электрических и магнитных сил, которые изменяются обратно пропорционально расстоянию от заряженной частицы, тогда как силы, имевшие место до остановки частицы, изменялись обратно пропорционально квадрату расстояния. Этот волновой импульс распространяется во вне со скоростью света и составляет, по моему мнению, рентгеновские лучи, которые появляются, когда отрицательно заряженные частицы из которых состоят катодные лучи, внезапно останавливаются, ударяясь о твердое препятствие.

Легко показать, что энергия, заключенная в волновом импульсе, равна 2(ev)²/3δ. Эта энергия излучается в пространство. Количество излучающейся энергии зависят от δ, толщины волнового импульса, т. е. от быстроты, с которой остановилась частица. Если частица остановилась мгновенно, вся энергия в поле поглотится волновым импульсом, будет излучена и во вне; если же она постепенно останавливалась, только часть энергии излучится в пространство, а остальная часть обратится в тепло в том месте, где катодные лучи остановились.

Легко показать, что количество движения в волне в какой-нибудь момент равно и противоположно количеству движения в поле вне волны. Так как в пространстве, сквозь которое прошла волна, нет никакого количества движения, то полное количество движения в поле после остановки частицы равно нулю.

Предыдущие рассуждения приложимы только к тому случаю, когда частица движется так медленно, что фарадеевские трубки до остановки частицы равномерно распределены. Однако эти же принципы позволят нам определить результаты остановки заряженной частицы во всех тек случаях, когда задано распределение фарадеевских трубок при равномерном движении.

Возьмем, для примера, случай, когда частица вначале движется со скоростью света. До остановки фарадеевские трубки были все сгруппированы в экваториальной плоскости движущейся частицы. Чтобы найти конфигурацию фарадеевских трубок через промежуток времени t, мы, поступая так же, как раньше, находим конфигурацию трубок для этого момента, если бы частица не остановилась. Трубки в этот случае были бы расположены в плоскости на расстоянии Vt впереди частицы.

Проведем две сферы, центры которых находятся в частице, а радиусы соответственно равны Vt и V(t – τ), где τ — время, затрачиваемое на остановку. За внешней сферой конфигурация трубок будет такая же, как если бы частица не остановилась, т.е. трубки будут в плоскости на расстоянии Vt впереди частицы; плоскость эта коснется внешней сферы. Внутри внутренней сферы трубки будут равномерно распределены, поэтому для сохранения непрерывности трубки внутри промежутка между сферами должны изгибаться, как это показано на рис. 14. Таким образом, мы имеем в этом случае две волны, одну — плоскую, распространяющуюся в том направлении, в каком частица двигалась до остановки, другую — сферическую, распространяющуюся во всех направлениях.

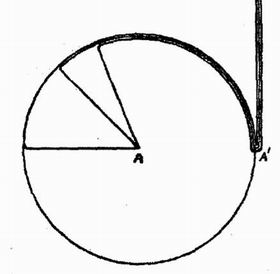
Рис. 14

Предыдущий метод может быть приложен и к тому случаю, когда заряженная частица, вместо того, чтобы остановиться, изменила каким-либо образом свою скорость. Так, если скорость частицы, вместо того, чтобы дойти до нуля, уменьшается на Δv, то можно показать, что это вызовет волну, в которой магнитная сила Н определяется уравнением Н = еΔv sinθ/rδ, а тангенциальная электрическая сила Т определяется уравнением Т = еΔv sinθ/Vrδ

Теперь, толщина волны δ есть пространство, пройденное светом в продолжение того промежутка времени, в течение которого скорость частицы менялась. Поэтому, если Δt есть время, нужное для того, чтобы вызвать изменение скорости Δv, то δ = VΔt и потому имеем: Н = еΔvsinθ/VΔt r, Т = еΔvsinθ/V²Δt r. Но Δv/Δt = f — ускорение частицы. Поэтому имеем: Н = –еfsinθ/rV, T = –еfsinθ/ rV².

Эти уравнения показывают, что заряженная частица с ускоренным движением вызывает волну электрических и магнитных сил, причем силы изменяются обратно пропорционально расстоянию от частицы.

Отсюда следует, что если заставить заряженное тело вибрировать таким образом, чтобы его ускорение периодически изменялось, то от заряженного тела будут исходить периодические волны электрических и магнитных сил. Согласно электромагнитной теории света, эти волны должны быть световыми волнами, если только периодические изменения в ускорении заряженного тела происходят с достаточной быстротой.

Тот метод исследования, который мы употребляли для определения влияния изменений в движении тела на конфигурацию фардеевских трубок, приводит нас к очень простому способу представления тех процессов, которые происходят при распространении световой волны в эфире. Мы рассматривали эти явления, как вызванные распространением поперечных колебаний вдоль туго натянутых фарадеевских трубок. Таким образом, мы должны были усвоить те же взгляды на распространение света, какие были выработаны самим Фарадеем, как это показывают следующие выдержки из статьи "Мысли о световых колебаниях".

"Взгляд, который я так смело предлагаю, рассматривает излучения, как очень тонкий род колебаний силовых линий, которые, как известно, соединяют частицы с массами".

Такой взгляд на свет, как на что-то, вызванное колебаниями туго натянутых фарадеевских трубок, возбуждает один вопрос, по моему, никем еще не отмеченный. Нельзя думать, что фарадеевские трубки, простирающиеся в эфире, всецело заполняют его. Надо скорее смотреть на них, как на отдельные нити, находящиеся в эфире и придающие последнему волокнистое строение. В таком случае с той точки зрения на световую волну, которую мы приняли, сама волна должна иметь известное строение, и фронт волны, вместо того, чтобы быть равномерно освещенным, должен был бы представлять серию светлых пятен на темном фоне, причем светлые пятна соответствовали бы тем местам, где фарадеевские трубки перерезают фронт волны.

Такой взгляд на строение световой волны может объяснять одно явление, которое меня всегда поражало, как весьма замечательное и трудно согласуемое со взглядом, что световая волна или, скорее в данном случае, рентгеновский луч не имеет определенного строения. Мы видели, что способ распространения и строение рентгеновского луча те же, что и у световой волны. Поэтому общие соображения относительно строения рентгеновских лучей могут быть применены и к световым волнам. Явление, о котором идет речь, следующее: рентгеновские лучи могут проходить довольно большие расстояния через газы, при этом прохождении они ионизируют газ, разбивая его молекулы на положительные и отрицательные ионы. Число расщепленных таким образом молекул, даже для сильных лучей, составляет чрезвычайно малую часть, меньшую, чем одна биллионная всех молекул газа. Теперь, если условия впереди волны однообразны, все молекулы газа находятся в одинаковых условиях. Почему же расщепляется только такая их незначительная часть?

Это можно объяснить тем, что расщепление происходит при наличии некоторого специального условия, например, если молекулы обладают количеством кинетической энергии, настолько превосходящим среднюю кинетическую энергию газовых молекул, что, согласно закону Максвелла о распределении кинетической анергии, их число должно быть чрезвычайно малым в сравнении с общим числом молекул газа. Но если бы в этом заключалась причина рассматриваемого явления, то самый закон распределения показывает, что число молекул, находящихся в ненормальных условиях, довольно быстро возрастает вместе с температурою, так что ионизация, созданная рентгеновскими лучами, должна быстро возрастать с температурою. Последние опыты М. Клунгa (M. Clung) в лаборатории имени Кавендиша показывают, что при увеличении температуры газа от 15°С до 200°С не произошло какого-либо заметного усиления ионизации, между тем, как число молекул, обладающих ненормально большим количеством энергии, чрезмерно возросло при таком повышении температуры. Трудность в объяснении этой слабой ионизации отпадает, если, вместо того, чтобы рассматривать фронт рентгеновской волны однообразным, мы предположим, что он состоит из очень ярких пятен, разделенных промежутками, где яркость очень мала, потому что в этом случае не только все молекулы, а, вероятно, даже разные части одной и той же молекулы, подвергаются различным условиям. Этот случай аналогичен пучку катодных лучей, проходящих через газ. При этом число молекул, приходящих в столкновение с лучами, может быть очень малой частью всего числа молекул.

Вернемся, однако, к случаю заряженной частицы с ускоренным движением. Мы уже видели, что из частицы выходят электрическая и магнитная силы и распространяются по радиусам со скоростью света и что силы и радиальные и магнитные перпендикулярны к тому направлению, в котором они распространяются. Но, так как каждая единица объема электромагнитного поля имеет количество движения, равное произведению из плотности фарадеевских трубок и магнитной силы, причем направление количества движения перпендикулярно к обеим этим величинам, то должно существовать в той волне, которая вызвана ускорением заряженной частицы, как и вообще во всякой электрической или световой волне, определенное количество движения в направлении распространения волны. Таким образом, если какая-нибудь волна, например, световая, поглощается тем веществом, сквозь которое проходит, то количество движения волны сообщится поглощающему веществу, которое будет поэтому испытывать силу, которая стремится его толкать по направлению распространения света. Так, когда свет падает нормально на поглощающее черное вещество, он отталкивает это вещество. Максвелл показал, что это отталкивание, вызываемое излучением, есть следствие электромагнитной теории света. Оно было недавно открыто и измерено Лебедевым при помощи очень красивых опытов, которые были подтверждены и разработаны Никольсом и Гуллем (Nichols, Hull).

Давление, испытываемое поглощающим веществом, пропорционально его площади, тогда как вес вещества пропорционален его объему. Поэтому, если мы линейные размеры уменьшим вдвое, то вес уменьшится в восемь раз, между тем как давление излучения уменьшится только в четыре раза. Поэтому, уменьшив достаточно размеры поглощающего тела, мы придем к такому положению, когда силы, обусловленные излучением, превзойдут те, которые, подобно весу, пропорциональны объему вещества. Исходя из этого принципа и зная напряженность солнечной радиации, Аррениус показал, что для непрозрачной сферы, плотность которой единица, а диаметр — 10 ^–5 см, давление, вызванное излучением Солнца, должно как раз уравновесить солнечное притяжение, между тем, как более мелкие тела должны отталкиваться от Солнца. Аррениус применил этот принцип к объяснению явлений, связанных с кометными хвостами. Пойнтинг недавно показал, что если две сферы, у которых плотность равна единице, а диаметр около 39 см, находятся при температуре в 27° С и защищены от внешних излучений, то отталкивание, вызванное излучениями сфер, превышает их взаимное тяготение, так что сферы будут отталкивать друг друга.

С другой стороны, когда свет преломляется и отражается от прозрачной поверхности, направление света, а потому и направление количества движения, изменяется, так что преломляющее вещество должно получить некоторое количество движения. Нетрудно доказать, что даже при наклонном падении света количество движения, сообщаемое веществу, нормально к отражающей поверхности. Есть немало интересных вопросов, связанных с силами, которые действуют на преломляющие призмы при прохождении через них света, вопросов, которые сами собой возникнут перед вами, когда вы будете рассматривать изменения в количестве движения, испытываемые световой волной при прохождении сквозь призму. Тангенциальные силы, обусловленные светом, до сих пор, насколько я знаю, не открыты еще экспериментально. Однако, в некоторых случаях они должны существовать, например, в том случае, когда световой луч, падающий наклонно, не вполне отражается от металлической поверхности.

Волны электрической и магнитной силы, которые излучает заряженная частица, движущаяся с ускорением, несут с собою запас энергии. Эта энергия излучается в пространство, так что частица постоянно теряет энергию. Легко показать, что скорость излучения энергии частицею равна 2(ef)²/3V, где e — заряд частицы, f — её ускорение, а V — скорость света. Если мы примем в расчет ту потерю энергии частицею, когда ее движение ускорено, мы найдем несколько интересных результатов. Так, например, если частица с массою m и зарядом e выходит из состояния покоя, под действием постоянной электрической силы Х, то частица не сразу достигнет ускорения Хe/m, как это было бы при отсутствии потери энергии излучением, напротив, ускорение частицы в самом начале равно нулю, и только по прошествии времени, порядка e²/Vm, частица получит заметную часть своего окончательного ускорения.

Тактим образом, скорость, с которой частица теряет энергию в продолжение времени e²/Vm, очень мала в сравнении с окончательной скоростью. Поэтому, если бы частица подверглась действию волны электрической силы, которой нужно было бы время, порядка e²/Vm, чтобы пройти через частицу, то количество энергии, излученной частицей, было бы гораздо меньшей частью энергии волны, чем это было бы, если бы волна для прохождения через частицу затратила время, многократно превышающее e²/Vm. Это обстоятельство имеет важное применение при объяснении большей проницательной способности "жестких" рентгеновских лучей в сравнении с "мягкими" лучами. "Жесткие" лучи соответствуют волновым импульсам небольшой толщины, "мягкие" лучи — толстым. Таким образом, меньшая часть энергии излучается заряженными частицами, когда через них проходят "жесткие" лучи, чем тогда, когда проходят "мягкие" лучи.

Применяя закон, что скорость излучаемой энергии равна 2(ef)²/3V, к случаю заряженной частицы, описывающей круговую орбиту под влиянием притягательной силы, изменяющейся обратно пропорционально квадрату расстояния, мы найдем, что в этом случае скорость радиации пропорциональна восьмой степени скорости или четвертой степени энергии. Поэтому потеря энергии излучением возрастает гораздо быстрее, чем энергия движущегося тела.

Глава IV. Атомное строение электричества

До сих пор мы занимались большей частью свойствами силовых линий, их натяжением, массою эфира, ими увлекаемого, распространением по ним электрических возмущений. В этой главе мы исследуем природу электрических зарядов, образующих начала и концы этих линий. Мы покажем, что есть серьезные основания для предположений, что эти заряды имеют, так сказать, атомное строение. Каждый заряд построен из некоторого конечного числа отдельные зарядов, равных между собою, подобно тому, как, согласно атомистической теории материи, какое-нибудь количество водорода построено из некоторого числа маленьких частиц, называемых атомами, причем все атомы равны между собою. Если этот взгляд на строение электричества правилен, то любой конец фарадеевской трубки будет тем местом, откуда исходит постоянное, определенное количество трубок или куда они приходят.

Рассмотрим сначала доказательства, которые дают законы электролиза жидкостей. Фарадей показал, что когда электричество проходит через жидкий электролит, количество отрицательного электричества, выделяемого на положительном электроде, как и положительного электричества, выделяемого на отрицательном, пропорционально числу атомов, выделяющихся на электроде. Рассмотрим сначала одновалентные элементы, как водород, хлор, натрий и т. д. Фарадей показал, что когда одно и то же число атомов этих элементов передает свои заряды электроду, то количество сообщенного электричества одно и то же, безразлично, были ли носителями его атомы водорода, хлора или натрия. Это указывает на то, что любой атом этих элементов несет с собою один и тот же электрический заряд.

Перейдем теперь к двухвалентным элементам. Мы находим опять, что ионы всех двухвалентных элементов несут один и тот же заряд, но определенное число ионов двухвалентного элемента несет вдвое больший заряд, чем тот, который переносит то же число ионов одновалентного элемента. Это показывает, что каждый ион двухвалентного элемента несет вдвое больший заряд, чем одновалентный ион; дальше, трехвалентный нон несет утроенный заряд одновалентного, и т.д. Таким образом, при электролизе растворов, заряды, переносимые ионами, будут или зарядами водородного иона, или двойными такими зарядами, или тройными и т. д. Заряды, с которыми мы встречаемся, представляют всегда целое кратное заряда, переносимого водородным атомом. Мы не встретим никогда дробной части этого заряда, Это замечательное обстоятельство показывает, как сказал Гельмгольц в своей лекции о Фарадее, что "если мы примем гипотезу, что элементарные вещества составлены из атомов, то не можем избегнуть того заключения, что электричество как положительное, так и отрицательное, разделяется на определенные элементарные частицы, которые играют роль атомов электричества".

Когда мы рассматриваем прохождение электричества через газы, доказательства в пользу атомного характера электричества будут еще серьезнее, чем в случае прохождения через жидкости, главным образом потому, что мы знаем больше о прохождении электричества через газы, чем через жидкости.

Рассмотрим некоторые свойства электропроводности газов. Когда газ приведен в состояние проводимости, например, под действием рентгеновских лучей, он остается, в этом состоянии после прекращения действия лучей довольно продолжительное время, что что дает возможность изучить его свойства. Мы находим, что можно газ лишить проводимости, если пропустить его через хлопчатобумажную вату или через трубу с водой. Таким образом, проводимость принадлежит чему-то, смешанному с газом, что может быть отфильтровано от него; затем, газ может лишиться проводимости при пропускании через сильное электрическое поле. Эти результаты показывают, что та составная часть, которою обусловлена проводимость газа, состоит из заряженных частичек и что проводимость происходит от движения этих частичек в электрическом поле. В лаборатории имени Кавендиша мы измерили электрический заряд, связанный с этими частицами.

Принцип этого впервые употребленного метода следующий. Если в какой-нибудь момент в газе находятся n таких частичек, заряженных положительно, и n, заряженных отрицательно, и если каждая них несет электрический заряд е мы можем легко электрическими методами определить nе, количество электричества одного данного знака, находящегося в газе. Один из методов, при помощи которых это может быть сделано, состоит в том, чтобы заключить этот газ между двумя параллельными металлическими пластинками, одна из которых изолирована. Теперь предположим, что мы внезапно электризуем другую пластинку до очень высокого потенциала. Эта пластинка будет теперь отталкивать положительные частицы в газе, и эти последние, до того, как они успеют соединиться с отрицательными частицами, устремятся на изолированную пластинку. Таким образом, весь положительный заряд в газе будет перенесен на изолированную пластинку, где может быть измерен электрометром. Если мы будем располагать способом для определения n, то будем в состоянии найти и е.

Метод, посредством которого я определил n основан на открытии Ч. Т. Р. Вильсона (С. Т. R. Wilson), что заряженные частицы действуют как ядра, вокруг которых конденсируются маленькие капельки воды, если частицы окружены влажным воздухом, охлажденным ниже точки росы. В воздухе, свободном от пыли, очень трудно, как показал Эйткен (Aitken), получить туман охлаждением влажного воздуха, потому что нет ядер для конденсации окружающих капелек. Однако, если в свободном от пыли воздухе находятся заряженные частицы, то на них будет осаждаться туман, хотя бы пересыщение было гораздо меньшем, чем то, которое необходимо, чтобы вызвать заметный эффект, когда заряженных частиц нет.

Таким образом, в достаточно пересыщенном влажном воздухе на заряженных частицах осаждается туман, и частицы делаются поэтому видимыми. Это есть первый шаг к тому, чтобы их подсчитать. Капельки, однако, слишком малы и слишком многочисленны, чтобы их можно было прямо сосчитывать. Между тем, можно косвенно определить их число следующим образом. Предположим, что имеем некоторое число этих частиц в свободном от пыли воздухе в замкнутом сосуде, причем воздух насыщен водяными парами. Предположим далее, что мы вызываем в сосуде внезапное расширение воздуха. Это вызывает охлаждение воздуха, он окажется пересыщен парами, и капли осядут на заряженных частицах. Теперь, если знаем величину вызванного нами расширения, можем подсчитать охлаждение газа, а затем количество осажденной воды. Таким образом, мы знаем объем воды, находившейся в капельках. Поэтому, если знаем объем одной капельки, можно вывести число капелек.

Чтобы найти размеры капельки, воспользуемся исследованием Джорджа Стокса (Geotge Stokes) о скорости падения маленьких шариков в воздухе. Вследствие вязкости воздуха маленькие тела падают чрезвычайно медленно, и чем меньше тело, тем медленней оно падает. Стоке показал, что если а есть радиус водяной капельки, то скорость ее падения в воздухе V определяется уравнением: V = 2ga²/3μ, где g = 981 — ускорение силы тяжести, μ = 0,00018 — коэффициент вязкости воздуха; таким образом, V = 1,21 · 10⁶a². Поэтому, если мы могли бы определить V, то определили бы и радиус, а, следовательно, и объем капли. Но V есть, очевидно, скорость, с которой облако, образовавшееся вокруг заряженных частиц, спускается вниз, и может быть легко измерено из наблюдений над движением вершины облака. Таким путем я нашел объем капельки, а затем — n — число частичек. Так как из электрических измерений было определено ne, то, зная n, можно было подсчитать значение e. Таким путем я нашел значение e равным 3,4 · 10 ^–10 электростатических CGS единиц.

Опыты были проделаны с воздухом, водородом, углекислотой и было найдено, что ионы имеют один и тот же заряд во всех этих газах, что является серьезным аргументом в пользу атомного характера электричества.

Заряд газообразного иона можно сравнить с зарядом, увлекаемым водородном ионом при электролизе растворов, следующим образом. Мы знаем, что прохождение одной электромагнитной единицы электрического заряда или 3 · 10¹⁰ электростатических единиц через подкисленную воду освобождает 1,23 куб. см водорода при температуре 18°С и давлении в 1 атмосферу. Если при этой температуре и давлении в одном куб. см газа находятся N молекул, то число водородных ионов в 1,23 куб. см есть 2,46 N, так что если Е есть заряд водородного иона при электролизе растворов, получим 2,46 NЕ = 3 · 10¹⁰.

[...]

Таким образом, Таунсенд нашел, что Nе одно и то же в воздухе, водороде, кислороде и в углекислоте, и средняя величина найденных им значений Nе была 1,22 · 10¹⁰. Мы видели, что если Е есть заряд водородного иона, то NЕ = 1,22 · 10¹⁰. Таким образом, эти опыты показали, что е = Е или что заряд газообразного иона равен заряду, увлекаемому водородный ионом при электролизе растворов.

Равенство этих зарядов было также доказано очень простым путем Г. А. Вильсоном (Н. A. Wilson), которой вводил каждую секунду в некоторый объем воздуха при очень высокой температуре измеренное количество пара металлических солей. Этот пар подвергался ионизации, и смесь воздуха и пара приобретала очень |значительную проводимость. Ток сквозь пар возрастал вначале вместе с электродвижущей силой, вызывавшей его движения сквозь газ, но это возрастание не шло до бесконечности. После того, как ток достигал известной величины, дальнейшее возрастание электродвижущей силы не вызывало изменений тока. Ток, как во всех случаях прохождения через газы, достигает наибольшей величины, называемой "током насыщения" и не будет увеличиваться до тех пор, пока электрическое поле, приложенное к газу, не достигнет той интенсивности, при которой сквозь газ начинают проскакивать искры. Вильсон нашел, что ток насыщения сквозь пары соли как раз равен тому току, который, проходя черев водяной раствор соли, разлагает в секунду такое же количество соли, какое впускалось каждую секунду в горячий воздух.

Нужно подчеркнуть, что этот результат дает нам способ определения постоянной Авогадро, который не зависит от какой-либо гипотезы относительно формы иди размеров молекул или от вида их взаимодействий. Если N есть эта постоянная, е — заряд какого-либо иона, тогда Nе = 1,22 · 10¹⁰, а так как мы видели, что e = 3,4 · 10 ^–10, то N = 3,9 · 10¹⁹.

Таким образом, изучаем ли мы прохождение электричества через газы или через жидкости, мы приходим к понятию естественной единицы или атома электричества. Все заряды представляют целое краткое этого атома, подобно тому, как масса какого-нибудь количества водорода есть целое кратное массы водородного атома.

Масса носителей электричества

Мы должны теперь перейти к рассмотрению природы систем, переносящих заряды, и для того чтобы иметь как можно более простые условия, начнем со случая газа, находящегося при очень низком давлении, когда движение частиц не задерживается столкновениями с молекулами газа. Предположим, что имеем частицу массы m, переносящую заряд е движущуюся в плоскости чертежа, и что на нее действует однородное магнитное поле, перпендикулярное к плоскости. Мы видели, что при этих обстоятельствах частица находится под действием механической силы, равной Hev, где H есть магнитная сила, а v — скорости частицы. Направление этой силы лежит в плоскости чертежа и перпендикулярно к траекторий частицы. Так как сила постоянно перпендикулярна к направлению движения частицы, скорость частицы, а поэтому и величина сипы, действующей на частицы, не изменяются, так что траектория частицы будет так же, как у тела, находящегося под действием постоянной нормальной силы. Легко показать, что эта траектория есть окружность, радиус которой определяется из уравнения a = mv/eH.

Скорость частицы может быть определена следующим образом. Предположим, что частица движется горизонтально в плоскости чертенка. В однородном магнитном ноле H, перпендикулярном к этой плоскости, на частицу будет действовать вертикальная сила, равная Hev. Если мы сверх магнитной силы, приложим вертикальную электрическую силу Х, то последняя будет производить на движущуюся частицу вертикальное механическое действие Хe. Сообщим Х такое направление, чтобы эта сила имела противоположное магнитной силе направление, и будем регулировать величину Х так, чтобы обе силы были равны. Мы можем узнать, что это расположение достигнуто потому, что в этом случае движение частицы под влиянием электрической и магнитной сипы таково, как будто обе эти силы отсутствовали. Когда обе силы равны, то мы имеем: Хe = Hev или v = Х/Н.

Поэтому, если мы имеем средства проследить движение частицы, то мы можем измерить радиус а круга, который она описывает под влиянием постоянной магнитной силы, и определить величину электрической силы, необходимой для того, чтобы уравновесить действие магнитной силы. Тогда вышеприведенные уравнения дадут нам возможность найти v и e/m.

Величина e/m для отрицательных наэлектризованных частиц в газах при низком давлении

Этим путей была определена величина e/m отрицательно заряженных частиц, образующих катодные лучи, которые составляют существенную часть электрического разряда через газ при низком давлении. Она была определена также для отрицательно наэлектризованных частиц, выделяемых металлами, 1) когда они подвергаются действию ультрафиолетовых лучей, 2) когда они нагреваются до температуры белого каления. Эти опыты привели к тому замечательному результату, что величина e/m остается неизменной, какова бы ни была природа газа, в котором находится частица, и какова бы ни была природа металла, из которого она выделилась. Во всех случаях, когда определялась величина e/m для отрицательно наэлектризованных частиц, движущихся со скоростью значительно меньше, чем скорость света, она всегда оказывалась постоянной около 10⁷, когда в качестве единиц выбирали сантиметр, грамм и секунду и когда заряд измерялся в электростатических единицах. Так как величина e/m для иона водорода при электролизе жидкостей составляет только 10⁴, и так как мы видели, что заряд газового иона равен заряду иона водорода при обыкновенном электролизе, то мы видим, что масса носителя отрицательного заряда должна быть равной приблизительно лишь тысячной доле атома водорода, долгое время считавшейся наименьшей, способной к самостоятельному существованию.

Для этих единиц отрицательного электричества я предложил название корпускул. Эти корпускулы всегда одинаковы, как бы ни возник электрический заряд, и где бы они ни находились. Таким образом, отрицательное электричество в газе при низком давлении имеет аналогичную структуру, как и газ, причем корпускулы играют роль молекул. Пользуясь старым названием, можно сказать, что «отрицательная электрическая жидкость» подобна газообразной жидкости с корпускулярной вместо молекулярной структурой.

Носители положительного электричества

Те же методы можно применить для определения величин e/m для носителей положительного электричества. Это сделал Вин (Wien) для положительного заряда, находимого в некоторых частях разряда в безвоздушной трубке, и я сам измерял e/m для положительного электричества, отдаваемого раскаленной проволокой. Результаты этих измерений представляют поразительный контраст с результатами измерений отрицательного заряда, так как вместо постоянной большой величины 10⁷, как при отрицательном заряде, e/m никогда не бывает больше 10⁴. Эту величину e/m может иметь, если носителем является атом водорода. Во многих случаях величина гораздо меньше 10⁴, показывая этим, что положительный заряд несут атомы, имеющие массу большую, чем масса водородного атома. Величина e/m варьирует с природой электродов и с газом в разрядной трубке точно так, как будто носителями положительного заряда были атомы элементов, которые случайно присутствовали при возникновении положительного заряда.

Эти результаты ведут нас к взгляду на электричество, имеющему поразительное сходство с теорией Франклина об «одной электрической жидкости». Но вместо того, чтобы подобно Франклину считать электрическую жидкость положительной, мы считаем ее отрицательной. "Электрическая жидкость" Франклина соответствует собранию корпускул, а именно, это собрание корпускул образует отрицательное электричество. Перенос заряда с одного места на другое вызывается движением корпускул от места, где имеется избыток положительного электричества, к месту, где есть избыток отрицательного. Положительно наэлектризованное тело есть такое, которое потеряло часть своих корпускул. Мы видели, что масса и заряд корпускул определены непосредственно опытом. В действительности мы теперь знаем об «электрической жидкости» больше, чем о жидкостях вроде воздуха или воды.