Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.1. Операции логики Буля

Объединение. Таблицы истинности

Объединением множеств A = {1, 2, 4, 6} и B = {2, 3, 4, 8, 9}

назовем множество

A ∪ B = {1, 2, 3, 4, 6, 8, 9},

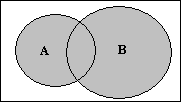
где ∪ — символ объединения множеств. Таким образом, объединением охватываются три класса элементов — C₁, C₂ и C₃, которые на диаграмме (рис. 1.3) заштрихованы.

Рис. 1.3

Логически операцию объединения двух множеств можно охарактеризовать словами: элемент x принадлежит множеству A или множеству B. При этом связка «или» одновременно означает и связку «и». Факт принадлежности элемента x множеству A обозначается как x ∈ A. Поэтому то, что x принадлежит A или/и B, выражается формулой:

x ∈ A ∪ B = (x ∈ A) ∨ (x ∈ B),

где ∨ — символ логической связки или, которая называется дизъюнкцией.

С точки зрения логики, вместо одной предметной переменной x удобно ввести две логические переменные x₁ и x₂. Областью определения x₁ и x₂ будут уже не числа натурального ряда, а только два логических значения: 1 для истинного значения и 0 для ложного.

Допустим, что x = 7. Поскольку это число не принадлежит ни множеству A, ни множеству B, то и логические значения переменных будут: x₁ = 0, x₂ = 0. Эта комбинация переменных отвечает классу C₀. Теперь предположим, что выбрано число 4. Оно входит как в A, так и в B. Следовательно, x₁ = 1, x₂ = 1, что соответствует классу C₃. Существуют еще два варианта, например, для числа x = 6 имеем x₁ = 1, x₂ = 0 и для x = 8 имеем x₁ = 0, x₂ = 1, которые отвечают классам C₁ и C₂.

Переменные x₁ и x₂ определяют некоторую логическую функцию:

y = f (x₁, x₂),

которая, в случае дизъюнкции, записывается как

y = x₁ ∨ x₂.

Легко усматривается, что число 7 не входит в объединенное множество A ∪ B, поэтому при x₁ = 0, x₂ = 0 значение логической функции y равно нулю. Когда же выбираются числа 4, 6 или 8, то все они непременно попадут в заштрихованную область диаграммы, следовательно, при этих значениях функция y равна единице. Все это удобно оформить таблицей (табл. 1.1), которую называют таблицей истинности.

Таблица 1.1

x1	x2	y = x1 ∨ x2
0	0	0
1	0	1
0	1	1
1	1	1

Между таблицей истинности и диаграммой Эйлера — Венна существует взаимно однозначное соответствие. Поэтому число единиц для y всегда будет совпадать с числом заштрихованных областей на диаграмме. Четыре комбинации аргументов x₁ и x₂ отвечают четырем областям C_i. Кроме того, нетрудно подсчитать, что число комбинаций нулей и единиц для функции y равно 16, значит и общее число возможных операций на двух множествах, т.е. число возможных функций y = f (x₁,  x₂) тоже равно этому же числу.