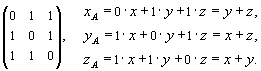
Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.1. Группа и связанные с ней понятия

Линейное преобразование

Линейное преобразование A вектора x в вектор y осуществляется с помощью квадратной матрицы:

y = Ax, где A = .                (2.1)

Если имеет место прямое преобразование (2.1), то должно существовать и обратное при условии, что матрица A имеет обратную:

y = A^–1 x.

Транзитивность линейного преобразования задает операцию умножения. Пусть даны два линейных преобразования:

z = Ay,         y = Bx,

Тогда существует третье преобразование C, которое получается путем перемножения A и B, т.е.

z = Ay = A(Bx) = (AB)x = Cx.         (2.2)

Выражение (2.2) стало возможным благодаря действию закона ассоциативности в отношении операторов A и B, а также вектора x. Наряду с выполнением закона (2.2), действуют еще три закона — один ассоциативности и два дистрибутивности:

A(λx) = (Aλ)x =(λA)x,         (2.3)

(A + B)x = Ax + Bx,    A(x + y) = Ax + Ay,

где λ – действительное или комплексное число.

Предположим, что матрица A в некотором базисе реализует линейное преобразование (2.1). В новом базисе это преобразование будет выглядеть иначе:

y' = A'x',             (2.4)

Обозначим через T матрицу перехода векторов из нового базиса в старый:

x = Tx',     y = Ty',     (2.5)

Подставим оба выражения (2.5) в преобразование (2.1), получим

Ty' = ATx'.             (2.6)

Умножим (2.6) слева на T^–1:

y' = T^–1ATx'.             (2.7)

Сравнивая равенства (2.4) и (2.7), окончательно находим:

A' = T^–1AT.            (2.8)

Линейное преобразование (2.8) называется прямым преобразованием подобия. Про матрицы A и A' говорят, что они подобны. Чтобы получить обратное преобразование подобия, нужно выражение (2.8) слева умножить на T, а справа — на T ^–1, в результате получим:

A = T A' T^–1.         (2.9)

Прямое и обратное преобразования обладают следующими свойствами, которые мы выпишем здесь только для прямого:

T^–1 (AB)T = (T^–1AT)(T^–1 BT),

T^–1 (A + B)T = T^–1AT + T^–1BT,     (2.10)

T^–1 A^–1 T = (T^–1AT) ^–1,     T^–1AⁿT = (T^–1AT)ⁿ.

Среди бесчисленного множества векторов x линейного преобразования (2.1) всегда найдется такой, что под действием оператор A вектор x перейдет в коллинеарный себе, т.е. если координаты преобразованного вектора отличаются от исходного только скалярным множителем λ:

Ax = λx.         (2.11)

В этом случае ненулевой вектор x называется собственным вектором оператора A, а число λ – его собственным значением. Равенство (2.11) эквивалентно системе уравнений:

(A – λE) x = 0,         (2.12)

которую можно использовать для нахождения собственных векторов x (здесь E — единичная матрица). Но прежде требуется найти все собственные значения оператора A. С этой целью составляют характеристический определитель, который затем разворачивается в характеристический многочлен — p(λ):

p(λ) = det(A – λE) = 0,    (2.13)

Корни многочлена (2.13) поочередно подставляются в систему (2.12). Решая ее отдельно для каждого собственного значения λ, находят соответствующие им собственные векторыx.

Собственные значения и собственные векторы часто ищутся с помощью процедуры диагонализации матрицы A. В результате этой процедуры все собственные значения оказываются расположенными на главной диагонали диагональной матрицы λ. Эта диагональная матрица также является линейным преобразованием типа (2.1), для которого остаются в силе свойства (2.2), (2.3) и, что особенно важно для нас сейчас, L связана с исходной матрицей A преобразованием подобия:

λ = T^–1AT.        (2.14)

В силу транзитивности преобразования подобия, т.е. если

C = S^–1BS,    B = R^–1AR   и   RS = T,

то оператор C связан с оператором A преобразованием подобия:

C = S^–1(R^–1AR)S = (RS) ^–1A(RS) = T^–1AT,

все подобные матрицы имеют одинаковые собственные значения.

Трансформационная матрица T, фигурирующая в преобразовании подобия (2.8), и матрица A в линейном преобразовании (2.1) на самом деле выполняют одинаковые функции, т.е. переводят одни векторы в другие. Далее мы будем рассматривать замкнутые по умножению группы линейных операторов, представленные в виде конечной совокупности матриц. С помощью преобразования подобия, в котором T пробегает все элементы группы, можно выявить класс эквивалентных операторов. В этом случае проявится относительное подобие. Но может получиться так, что рассматриваемая группа операторов является лишь подгруппой более обширного замкнутого множества. Тогда преобразование подобия по более широкой группе пополнит класс подобных операторов другими элементами. Диагональный оператор λ, не являясь элементом рассматриваемой группы операторов, может символизировать предельно широкий класс подобных элементов, не входящих в данную группу операторов. Таким образом, процедура диагонализации матриц позволяет разбить группу операторов на несколько непересекающихся абсолютных классов подобных элементов с одинаковыми наборами собственных значений. Абсолютные классы либо совпадают, либо шире относительных.

В дальнейшем нам часто придется иметь дело с матрицами, поэтому напомним основные действия с ними. Правило перемножения матриц продемонстрируем на числовых примерах. Пусть даны две матрицы —

A = ,     B = .

Перемножим их слева направо, как они записаны, получим:

AB = =

= = .

Теперь умножим их справа налево —

BA = =

.

Про матрицы A и B говорят, что они не коммутируют, поскольку AB ≠ BA. Две другие матрицы – A₁ и B₁ – коммутируют друг с другом, в чем можно убедиться путем их перемножения:

A₁ = ,    B₁ = ,    A₁B₁ = B₁ A₁.

Рассмотрим преобразование подобия. Пусть исходный базис выражается через φ, а новый — через φ':

;

;

.

Тогда трансформационная матрица T и обратная ей T–1 выглядят следующим образом:

T = ,     T^–1 = .

Наша трансформационная матрица T относится к ортонормированным, т.е. возведение любой строки или столбца в квадрат дает единицу, а перемножение различных строк и столбцов — ноль:

,

.

Для ортонормированных матриц (а именно с такими мы чаще всего будем иметь дело) обратная матрица получается путем транспонирования исходной.

Пусть, далее, в старом базисе φ действует операторA, который переводит координаты x, y, z в координаты x_A,y_A, z_A:

A =

В новом базисе оператор A , согласно (2.9), превратится в A':

A' = T AT^–1 =λ = .

В новом базисе действие оператора A' сводится к умножению всех координат на числа. Фактически, мы нашли собственные значения матрицы A, поскольку диагональная матрица A' является одновременно матрицей λ:

Всю процедуру трансформации координат можно провести на уровне преобразования соответствующих векторов, не прибегая в явном виде к формуле преобразования подобия. В самом деле,

= 

= ;

= 

= ;

= 

= .

Последние выкладки призваны также показать, что любые преобразования — будь то A, A', T — не существуют сами по себе, но всегда предполагают присутствие базисных векторов.

Обращаем внимание на то, что сумма диагональных элементов матрицы A (она именуется характером матрицы A) равна сумме диагональных элементов матрицыA'. И это неслучайно: характеры подобных матриц всегда одинаковы. Равенство характеров позволяет проверить правильность нахождения собственных значений.

Перестановка строк матрицы с одновременной перестановкой соответствующих столбцов (а такая процедура также относится к преобразованию подобия) не меняет внутренней природы матрицы. Эта трансформация не влияет и на собственные значения. Если матрица A имела собственные значения λ, то эквивалентная ей матрица A' будет иметь ту же самую матрицу λ, в которой собственные значения окажутся на новых местах. Перестановка строк и столбцов возможна постольку, поскольку она не меняет связи диагональных элементов с недиагональными. Пусть в матрице A элемент a₂₃ связывает элементы a₂₂ и a₃₃ , тогда после нового размещения элементов на диагонали в матрице A' указанная связь должна сохраниться:

A = ,    A' = ,    λ = .