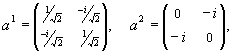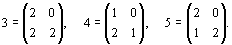
Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.1. Группа и связанные с ней понятия

Определение группы и примеры групп

Сейчас мы достаточно подготовлены, чтобы ввести определение группы. Группой называется операционное множество, в котором действует процедура умножения и которое подчинено следующим четырем условиям:

1) замкнутости: для каждой пары элементов g₁ и g₂ из группы G однозначно определено произведение g₁g₂ = g₃; причем элемент g₃ тоже должен обязательно принадлежать группе G, т.е.

g₁, g₂ ∈ G, g₁g₂ = g₃ ∈ G.

2) наличия тождественного элемента e: среди множества элементов группы G должен найтись такой элемент e, что для всякого g из G справедливы равенства:

eg = g,     ge = g;     e, g ∈ G.

3) наличия обратных элементов: для всякого g из G должен отыскаться единственный ему обратный элемент g^–1, принадлежащий G, при умножении на который получился бы тождественный элемент e; суть данного положения математически выражается следующим образом:

e = g g^–1,     e = g^–1g;     e, g, g^–1 ∈ G .

4) ассоциативности: для любых трех элементов g₁, g₂ и g₃ из G справедливо равенство:

g₁(g₂ g₃) = (g₁g₂)g₃.

Последнее условие выполняется для квадратных матриц, в чем можно убедиться путем перемножения, в частности, матриц размерности 2 × 2:

(AB)C = =

= A(BC) = ,

где

Аналогичная процедура доказательства распространяется на матрицы любой размерности. 

Ниже приводятся восемь степеней одной и той же матрицы a:

Выписанные матрицы составляют операционное множество, подчиненное четырем групповым условиям. В роли тождественного элемента выступает единичная матрица a⁸ = e. Перед нами коммутативная группа A восьмого порядка с таблицей умножения — табл. 2.1. Субстанционным множеством для нее являются восемь базисных векторов (первые столбцы матриц), которые переходят друг в друга под действием преобразований aⁱ:

,

.

Таблица 2.1

A	a1	a2	a3	a4	a5	a6	a7	a8
a1	a2	a3	a4	a5	a6	a7	a8	a1
a2	a3	a4	a5	a6	a7	a8	a1	a2
a3	a4	a5	a6	a7	a8	a1	a2	a3
a4	a5	a6	a7	a8	a1	a2	a3	a4
a5	a6	a7	a8	a1	a2	a3	a4	a5
a6	a7	a8	a1	a2	a3	a4	a5	a6
a7	a8	a1	a2	a3	a4	a5	a6	a7
a8	a1	a2	a3	a4	a5	a6	a7	a8

Например, 8 = a³ · 5, 7 = a⁵ · 2, a⁵ = a³ · a², или подробно:

,

.

Подмножества {a², a⁴, a⁶, a⁸} и {a⁴, a⁸} образуют подгруппы в группе A, поскольку элементы этих подмножеств удовлетворяют всем необходимым групповым условиям – замкнутости, ассоциативности, наличию в указанных подмножествах тождественного и обратных элементов.

Приведем множество B, которое также состоит из восьми матриц, полученных путем циклического возведения в степень матрицы b:

Множество B составляет группу, изоморфную группе A, поскольку ее элементы тоже перемножаются в соответствии с табл. 2.1 (если в последней символ a заменить на b). В группе B, как и в группе A, имеются две подгруппы из четырех и двух элементов. Примечательной особенностью циклической группы B является то, что в качестве тождественного элемента здесь выступает не единичная матрица, а ничем не примечательная матрица b⁸ = e. Если матрицу, обозначенную в списке как b³ (или b⁵, или b⁷), взять за образующую, то матрица, обозначенная как b⁸, по-прежнему будет выполнять роль тождественного элемента.

Транспонируем матрицы bⁱ. Получим новую циклическую группу C, изоморфную как группе B, так и группе A. Табл. 2.2 демонстрирует тоже циклический закон умножения исходных (bⁱ ) и транспонированных (c^j ) матриц: d^k = bⁱ · c^j,

Таблица 2.2

d k	c 1	c 2	c 3	c 4	c 5	c 6	c 7	c 8
b 1	d 2	d 3	d 4	d 5	d 6	d 7	d 8	d 1
b 2	d 3	d 4	d 5	d 6	d 7	d 8	d 1	d 2
b 3	d 4	d 5	d 6	d 7	d 8	d 1	d 2	d 3
b 4	d 5	d 6	d 7	d 8	d 1	d 2	d 3	d 4
b 5	d 6	d 7	d 8	d 1	d 2	d 3	d 4	d 5
b 6	d 7	d 8	d 1	d 2	d 3	d 4	d 5	d 6
b 7	d 8	d 1	d 2	d 3	d 4	d 5	d 6	d 7
b 8	d 1	d 2	d 3	d 4	d 5	d 6	d 7	d 8

Однако вся совокупность из 24 матриц B, C, D и даже отдельно 8 матриц D не образуют групп, поскольку в указанных множествах, во-первых, нет тождественного элемента (во всяком случае общего на все элементы), во-вторых, произведения элементов этих множеств равны нулевой матрице, которая, согласно групповым условиям, не может входить в состав групп:

cⁱ · bⁱ = dⁱ · d^j = .

Таким образом, произведение элементов двух групп породило негрупповое множество D:

Приведем пример некоммутативной группы D₃ на матрицах, элементами которых являются числа 0 и 1. Здесь при перемножении матриц следует учитывать, что сложение осуществляется по mod (2), т.е. сумма 1 + 1 = 0. То, что группа D₃ не коммутативна, видно из ее таблицы умножения (табл. 2.3), в которой не все элементы расположены симметрично относительно главной диагонали. Причем данная группа относится к весьма распространенному типу групп, имеющих общепринятое обозначение D₃ и названных Клейном группами диэдра:

Таблица 2.3

D3	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	0	3	2	5	4
2	2	4	0	5	1	3
3	3	5	1	4	0	2
4	4	2	5	0	3	1
5	5	4	3	2	1	0

Таблица 2.4

C6	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	4	3	5	0	2
2	2	3	0	1	5	4
3	3	5	1	4	2	0
4	4	0	5	2	1	3
5	5	2	4	0	3	1

Если в качестве образующего элемента из выписанных матриц взять матрицу, обозначенную цифрой 1, а при перемножении матриц использовать сложение по mod (3), когда 1 + 2 = 0, 2 + 2 = 1, то получим циклическую, а значит, коммутативную группу с общепринятым обозначением — C₆:

, 

Таблица умножения элементов группы C₆ (табл. 2.4) уже будет симметричной относительно своей главной диагонали.

Приведенных примеров, по-видимому, достаточно, чтобы усвоить понятие группы. Занимаясь морфологическим анализом групп, мы позже убедимся, какую исключительно важную роль играет при этом преобразование подобия или, как часто его называют, трансформационное преобразование (2.8). Оно позволяет группу G, состоящую из элементов { ..., u, v, w, x, y, z}, разбить на классы эквивалентности. Отношение эквивалентности предполагает выполнение трех законов – рефлексивности (каждый элемент a равен самому себе: a = a), симметричности (если a = b, то и b = a) и транзитивности (если a = b и b = c, то a = c). Все три закона выполняются для преобразования подобия, которое для группы G с указанными элементами запишется как

x = z^–1yz.         (2.15)

В теории групп в этом случае принято говорить, что элемент x сопряжен элементу y посредством элемента z. Закон рефлексивности выполняется для преобразования подобия (2.15) в силу непременного существования в группе G такого элемента z, что x = z^–1xz, в частности, когда z = e. Для того чтобы убедиться в справедливости закона симметричности, достаточно преобразование (2.15) умножить справа на z^–1 и слева на z, получим y = zxz^–1 . Но так как всякий элемент z имеет себе обратный (w), последнее равенство можно переписать в нужном нам виде, т.е. как (2.15): y = w^–1xw.

Наконец, проверим выполнение закона транзитивности, который в данном случае формулируется следующим образом:

если x = z^–1yz и y = v^–1uv, то x = w^–1uw.

Это возможно в силу

x = z^–1yz = z^–1 (v^–1uv)z = (z^–1v^–1)u(vz) = (vz)^–1u(vz) = w^–1uw.

В коммутативных группах каждый элемент образует свой собственный класс сопряженности, так что число классов равно порядку т.е. числу элементов группы: x = z^–1yz = z^–1zy = y. Отсюда разбиение группы на относительные классы эквивалентности начальных пяти порядков заранее предрешено, так как все они коммутативны. Впервые некоммутативность между элементами встречается в группе диэдра D₃, которая состоит, как мы уже видели, из шести элементов.