Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.1. Группа и связанные с ней понятия

Матричные конструкции

Для практических упражнений удобно воспользоваться системами из a и b 0,1-матриц 8-го порядка, свернутых до матриц 4 · 4, которые по отдельности образуют некоммутативные подгруппы 8-го порядка, а все вместе — группу 32-го порядка:

, ,

, ;

, ,

, ;

В группе и подгруппах выполняются следующие соотношения:

a_ia_j = –a_ja_i = a_k,     b_ib_j = –b_jb_i = b_k, a_ib_j = b_ja_i,

,     ,     ,     .

Группы можно уменьшить, если использовать матрицы 3 · 3 и 2 · 2, или, напротив, увеличивать, если добавлять матрицы 4 · 4, но с нечетным числом положительных и отрицательных единиц или с мнимой единицей. Интересные системы образуют матрицы совершенно иной природы:

,

,

;

, ...

Матрица, описывающая структуру электромагнитного поля, может быть разложена по базисным 0,1-матрицам соответствующих координат:

=

= H₁ + ... + E₃.

Аналогично, составляются агрегаты из a и b матриц:

A = p₀a₀ + p₁a₁ + p₂a₂ + p₃a₃ = ,

B = q₀b₀ + q₁b₁ + q₂b₂ + q₃b₃ = .

Обратимся к вопросу о собственных значениях. Ранее мы показали, что всякую матрицу z вида:

можно рассматривать в качестве комплексного числа. Несложно подобрать для z такую трансформационную матрицу T , чтобы с ее помощью осуществить преобразование подобия, результатом которого были бы собственные значения Λ = T^–1zT:

= .

Аналогичного результата можно добиться, если для матрицы z составить характеристический определитель и затем отыскать корни характеристического уравнения. Для определителя размерности 2 · 2 действует простая формула, которая приводит к предыдущему результату:

Есть и еще один способ нахождения собственных значений. Для этого с помощью замены (2.16) увеличим матрицу z размерности 2 · 2 до размерности 8 · 8, при этом все x снабдим индексами, чтобы можно было видеть, каким образом следует производить перестановку строк и столбцов для получения нужной структуры:

z =

= =

= .

Собственными значениями 0,1-матриц являются корни n-ой степени из единицы. Если какая-либо 0,1-матрица a обращается в единичную матрицу e при показателе степени, равном, скажем, четырем, то собственными значениями матрицы a будут четыре корня из единицы. Матрицы, обладающие одинаковыми наборами собственных значений, подобны между собой, причем они образуют абсолютные классы эквивалентности, хотя сами матрицы могут быть элементами коммутативных групп, где каждый элемент, как известно, образует свой относительный класс эквивалентности. Приведем несколько базисных 0,1-матриц и рядом с ними выпишем наборы их собственных значений:

.

Таким образом, наборы собственных значений базисных 0,1-матриц однозначно характеризуют периодичность матрицы.

На основе замены (2.16) можно получить многие важные математические результаты, которые, быть может, непосредственно и не связаны с группами. Так, легко показать, что матрицы вида

имеют одинаковые наборы собственных значений, поскольку все три матрицы после разворачивания и соответствующей перестановки диагональных элементов обнаруживают свою идентичность:

,

,

.

Несложно убедиться в справедливости цепи эквивалентных числовых матриц:

.

Полученные результаты распространяются на матрицы больших размерностей. Кроме того, следует иметь в виду, что любую эрмитову матрицу (H) можно представить комплексным числом из матриц симметричной (S) и кососимметричной (K) структуры:

.

Завершим этот раздел двумя нетривиальными примерами.

Пример 1. Перемножим две матрицы A и B с вещественными, в том числе, и отрицательными матричными элементами. Далее, используя замену (2.16), развернем матрицы A и B до матриц A₁ и B₁ и вновь их перемножим. Для всех результирующих матрицC, C₁ и C₂ найдем собственные значения, которые выпишем в табл. 2.12.

.

Таблица 2.12

Собст. значения C	Собст. значения C1	Собст. значения C2
– 0.0481 + 51.9424i	– 0.0481 + 51.9424i	– 0.0481 + 51.9424i
– 0.0481 – 51.9424i	– 0.0481 – 51.9424i	– 0.0481 – 51.9424i
–20.9338	–20.9338	–20.9338
—	195.3817	122.02
—	0.4562	16.3986
—	–13.9279	–28.2267

Комментарий к примеру 1. Процедура умножения матриц A на B и A₁ на B₁ дала почти один и тот же результат: матрицы C, C₁ и C₂ эквивалентны, на что указывает наличие в их собственных значениях трех одинаковых чисел. Однако есть и неэквивалентная компонента. Это связано с тем, что развернутые матрицы C₁ и C₂ несут более обширную информацию, чем матрица C. Поэтому мы говорим, что матрицы C₁ и C₂ подобны (гомоморфные) C.

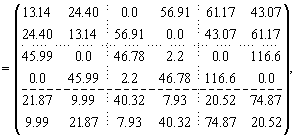
Пример 2. Пусть дана эрмитова матрица H; найдем ее собственные значения Λ. Затем комплексную матрицу H развернем в вещественную матрицу H₁ с отрицательными элементами и снова найдем собственные значения Λ₁. Наконец, найдем собственные значения Λ₂ матрицы H₂ с положительными элементами, полученными по формуле (2.17).

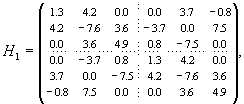
Диагональные элементы матрицы Λ₂ равны:

2.75,     2.75,     9.54,     9.54,     –13.69,     –13.69,     2.25,     1.82,     1.09,     10.46,     –7.81,     19.79.

Комментарий к примеру 2. Если применительно к H₁ воспользоваться заменой (2.16) вместо (2.17), то у вновь получившейся матрицы были бы точно такие же собственные значения, что и у матрицы H₂. Это говорит о том, что для нахождения собственных значений важна именно связь диагональных элементов с недиагональными. При переходе от матрицы H к матрице H₁ собственные значения просто удвоились, а при переходе от H₁ к H₂ добавились шесть различных вещественных значений. В примере 1 дополнительные собственные значения также появились за счет структурной перестройки матриц, которая привела к положительным матричным элементам. Таким образом, требование о недопустимости смешения положительных и отрицательных чисел породило неэквивалентную процедуру. Здесь матрица H₁ изоморфна исходной матрице H, в то время как матрица H₂ только гомоморфна H.