Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.1. Группа и связанные с ней понятия

Гиперкомплексные числа

Базисная 0,1-матрица отрицательного числа получалась путем удвоения размерности базисной 0,1-матрицы положительного числа. Комплексное число получилось за счет удвоения суммы положительного и отрицательного чисел, что можно представить формулой:

x = [х₀e + х₁(–e)] + [х₂e + х₃(–e)]i.

Теперь рассмотрим гиперкомплексное число, которое называется кватернионом и которое получается путем удвоения комплексного числа:

x = {[х₀ e + х₁(–e)] + [х₂e + х₃(–e)] i} + {[х₄e + х₅(–e)] +

+ [х₆e + х₇(–e)] i}j = х₀ e + х₁ (–e) + х₂i + х₃(–i) +

+ х₄j + х₅(–j) + х₆k + х₇(–k).

Приведем таблицу умножения (табл. 2.9) и таблицу базисных единиц (табл. 2.10) кватерниона.

Таблица 2.9

e	–e	i	–i	j	–j	k	–k
–e	e	–i	i	–j	j	–k	k
i	–i	–e	e	k	–k	–j	j
–i	i	e	–e	–k	k	j	–j
j	–j	k	–k	–e	e	i	–i
–j	j	–k	k	e	–e	–i	i
k	–k	j	–j	–i	i	–e	e
–k	k	–j	j	i	–i	e	–e

Таблица 2.10

e	–e	i	–i	j	–j	k	–k
–e	e	–i	i	–j	j	–k	k
–i	i	e	–e	–k	k	j	–j
i	–i	–e	e	k	–k	–j	j
–j	j	k	–k	e	–e	–i	i
j	–j	–k	k	–e	e	i	–i
–k	k	–j	j	–i	i	e	–e
k	–k	j	–j	i	–i	–e	e

Сравнивая обе таблицы, можно заметить, что они отличаются друг от друга только порядком строк. Отсюда вывод: для построения таблицы базисных 0,1-матриц необходимо строки и столбцы таблицы умножения упорядочить так, чтобы все ее тождественные элементы оказались на главной диагонали.

На основе табл. 2.10 можно выписать полную систему базисных единиц кватерниона. В частности, для базисной единицы k 0,1-матрица выглядит следующим образом:

k = .

Аналогично сворачиваются все остальные базисные единицы. Полная система единиц на свернутых матрицах кватерниона имеет вид:

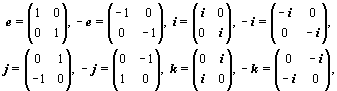
Приведенные матрицы образуют антикоммутативную группу, так как, согласно табл. 2.9, имеем:

ij = k,     ji = –k,     jk = i,     kj = –i,     ik = –j,     ki = j.

Приведем обобщенную формулу перемножения двух кватернионов x и y, по которой отрицательные и положительные компоненты числового агрегата уже не перемешиваются:

(х₀у₀ + х₁у₁ + х₂у₃ + х₃у₂ + х₄у₅ + х₅у₄ + х₆у₇ + х₇у₆) · e +

+ (х₀у₁ + х₁у₀ + х₂у₂ + хх₃у₃ + х₄у₄ + х₅у₅ + х₆у₆ + х₇у₇) · (–e) +

+ (х₀у₂ + х₁у₃ + х₂у₀ + х₃у₁ + х₄у₆ + х₅у₇ + х₆у₅ + х₇у₄) · i +

+ (х₀у₃ + х₁у₂ + х₂у₁ + х₃у₀ + х₄у₇ + х₅у₆ + х₆у₄ + х₇у₅) · (–i) +

+ (х₀у₄ + х₁у₅ + х₂у₇ + х₃у₆ + х₄у₀ + х₅у₁ + х₆у₂ + х₇у₃) · j +

+ (х₀у₅ + х₁у₄ + х₂у₆ + х₃у₇ + х₄у₁ + х₅у₀ + х₆у₃ + х₇у₂) · (–j) +

+ (х₀у₆ + х₁у₇ + х₂у₄ + х₃у₅ + х₄у₃ + х₅у₂ + х₆у₀ + х₇у₁) · k +

+ (х₀у₇ + х₁у₆ + х₂у₅ + х₃у₄ + х₄у₂ + х₅у₃ + х₆у₁ + х₇у₀) · (–k).

Удвоение комплексного числа можно понимать иначе, а именно, как удвоение длины цикла с 4 до 8. Тогда новое гиперкомплексное число будет иметь таблицу умножения в виде табл. 2.11. 

Таблица 2.11

e	–e	i	–i	j	–j	k	–k
–e	e	–i	i	–j	j	–k	k
i	–i	–e	e	k	–k	–j	j
–i	i	e	–e	–k	k	j	–j
j	–j	k	–k	i	–i	–e	e
–j	j	–k	k	–i	i	e	–e
k	–k	–j	j	–e	e	–i	i
–k	k	j	–j	e	–e	i	–i

Эта таблица умножения симметрична относительно главной диагонали, в отличие от предыдущего случая. Это значит, что умножение двух гиперкомплексных чисел, построенных на базисных единицах табл. 2.7, будет уже коммутативным.

Две следующие группы базисных единиц —

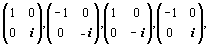
и

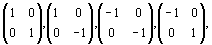
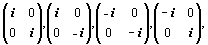
изоморфны между собой, в чем можно убедиться, если составить для них таблицы умножения, сохранив при этом приведенный порядок элементов. Далее, если оба ряда матриц перемножить между собой, возникнут еще четыре матрицы:

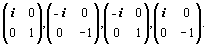
Объединив эти матрицы с двумя предыдущими рядами, получим новый коммутативный базис из 16 различных матриц.

Процедуру удвоения элементов группы можно продолжить, например, и так: удвоенные базисные единицы кватерниона —

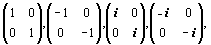
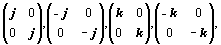
дополнить либо матрицами вида:

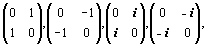
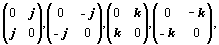
либо другими матрицами —

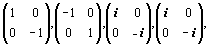
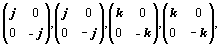
В обоих случаях получается некоммутативный базис из 16 матриц.