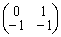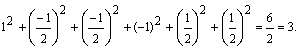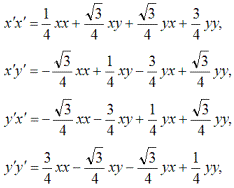
Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.2. Группы на матрицах и подстановках

Прямая сумма и прямое произведение

Можно подобрать такую трансформационную матрицу t, которая разобьет все 0,1-матрицы представления E₄ на сумму E₀ и E₃: 

E₀ + E₃ = t E₄ t^–1.

В частности, для элемента a группы D₃ будем иметь разложение:

E₄(a) = E₀(a) + E₃(a) = =

= .

Если все матрицы одного представления E_α под действием трансформационной матрицы t разлагаются на сумму двух или большего числа других представлений (E_β + E_γ + ... ), то говорят, что представление E_α — приводимо. Если матрицы представлений E_β, E_γ и т.д. больше нельзя разложить на меньшие матрицы, значит, они являются неприводимыми. Так, все матрицы представлений E₀, E₁, E₂ и E₃ — неприводимы, поскольку невозможно найти такую трансформационную матрицу t, чтобы в результате преобразования из них получились матрицы меньших размерностей. Заметим, что под «суммой» матричных представлений следует понимать прямую сумму матриц, т.е. когда приводимая матрица трансформируется в блочно-диагональную.

Про представления E₂ и E₃ было сказано, что они эквивалентны, т.е. существует такая матрица t₁, которая способна трансформировать все матрицы E₂ в матрицы E₃, и наоборот:

E₃ = t₁ E₂ t₁^–1,     E₂ = t₁^–1 E₃ t₁,

Такая матрица t₁ существует. Продемонстрируем действие этой матрицы на элементе a:

= .

Таким образом, все матрицы представлений E₃ и E₄ в табл. 2.46 взаимно связаны с ортогональным неприводимым представлением E₂. Единичное представление E₀ образовано базисом —

.

Базисом другого одномерного представления (E₁) служит ось z. Оси x и y являются базисом для матриц E₂. Если учесть, что координаты на плоскости преобразуются по известным формулам:

x' = x cosφ – y sinφ,    y' = x sinφ + y cosφ,

то при повороте на угол 2π/3, имеем

тогда преобразование координат примет вид:

= · . 

Вершины треугольника (рис. 2.5а) имеют координаты:

0 = ,     1 = ,     2 = ,

причем 2 = – 0 – 1. Этим вершинам соответствуют три неортогональных вектора — 0, 1 и 2, которые образуют базис для представлений E₃ и E₄. Ортогональное представление E₂(a) и неортогональное E₃(a) преобразуют свои системы базисных векторов: 

= · ,     = · .

Следует также напомнить, что существует так называемая активная система координат, когда объект (например, наш треугольник) находится в покое, а координатные оси вращаются вокруг него; и пассивная, когда система координат покоится, а объект вращается внутри нее. Кроме того, для согласования действия подстановок и матричных преобразований может помочь противоположная расстановка сомножителей либо для матриц, либо для подстановок, т.е. для выполнения одного и того же группового преобразования для подстановок берется произведение ab, а для матриц — ba (или наоборот).

Если неприводимое матричное представление ортонормировано, то оно подчиняется следующему фундаментальному тождеству: 

         (2.30)

где g — элементы группы G, n — порядок группы G,

n_α — размерность матриц представления E_α,

— матричные элементы представлений,

δ_xy — символ Кронекера (при x = y, δ_xy = 1, при x ≠ y, δ_xy = 0)

Проиллюстрируем справедливость (2.30) на наших конкретных ортонормированных неприводимых представлениях E₁ и E₂:

= 0 и = 3,

поскольку

Теперь, в соответствии с таблицей умножения элементов группы D₃, построим одну 0,1-матрицу регулярного представления E₅(a) (аналогичным образом находятся все остальные матрицы приводимого представления E₅):

.

Существует такая трансформационная матрица T, которая позволит все матрицы E₅ разложить на матрицы неприводимых представлений E₀, E₁, E₂. Для нахождения элементов матрицы T пользуются элементами матриц E₀, E₁, E₂ (табл. 2.46) и формулой —

.         (2.31)

Произведем разложение матрицы E₅(a) на неприводимые представления, используя конкретную трансформационную матрицу (2.31), получим:

E'₅(a) = T^–1 · E₅(a) · T = E₀(a) + E₁(a) + 2 · E₂(a),     (2.32)

где E'₅(a) — блочно-диагональная матрица, имеющая вид:

E'₅(a) = .

Трансформационная матрица T выглядит так

T = .

Таким образом, все регулярные матрицы E₅(g) распадутся на прямую сумму блоков, причем каждый из блоков неприводимого представления E_α(g) входит в блочно-диагональную матрицу E'₅(g) ровно n_α раз. В нашем случае размерности представлений n_α равны: n₀ = n₁ = 1, n₂ = 2.

Наряду с прямой суммой можно ввести понятие о прямом произведении матриц. Пусть даны две матрицы A и B:

     .

Определим их прямое произведение следующим образом:

=

= .

В частности,

E₂(a) · E₂(a) = =

=

Ортонормированный базис двухмерного неприводимого представления E₂(a) имеет вид:

Если составить всевозможные произведения x' и y',

то станет понятен и смысл матрицы прямого произведения. Добавим, что при прямом перемножении свойство ортонормированности сохраняется.

Сумма матриц прямых произведений образует новое представление группы D₃, причем приводимое, которое мы обозначим как 

E₆(a) = E₂(a) · E₂(a).

Приводимость означает, что матрицы E₆ (a, b, ...) каким-то образом раскладываются в прямую сумму неприводимых представлений. Чтобы уметь решать подобного рода задачи, необязательно искать соответствующие трансформационные матрицы типа (2.31). Достаточно знать характеры матричных представлений по трем классам эквивалентности C₀, C₁ и C₂ группы D₃. Затем, для определения числа неприводимых представлений E_α, содержащихся в приводимом E_β, необходимо воспользоваться простым соотношением:

       (2.33)

где , n — порядок группы G, h_α и h_β — характеры представлений E_α и E_β, которые приведены в табл. 2.47.

Таблица 2.47

По формуле (2.33) найдем коэффициенты m_α сначала для приводимого представления E₄.

m₀ = (1/6) · [3 · 1 + 0 · 1 + 0 · 1 + 1 · 1 + 1 · 1 + 1 · 1] = 1,

m₁ = (1/6) · [3 · 1 + 0 · 1 + 0 · 1 + 1 · (–1) + 1 · (–1) + 1 · (–1)] = 0,

m₂ = (1/6) · [3 · 2 + 0 · (–1) + 0 · (–1) + 1 · 0 + 1 · 0 + 1 · 0] = 1.

Отсюда получаем, что E₄ = E₀ + E₂. Аналогичным расчетом убеждаемся в справедливости еще одного известного разложения (2.32):

E₅ = E₀ + E₁ + 2 · E₂.

В случае прямого произведения формула (2.33) не меняется, и результат будет следующим:

E₆ = E₂ · E₂ = E₀ + E₁ + E₂.

Для нахождения характеров представления E₆ необязательно искать матрицы прямых произведений E₂ · E₂. Достаточно строку характеров E₂ (табл. 2.47) возвести в квадрат. Все другие разложения приводимых представлений (E₄ и E₅) на неприводимые (E₀, E₁, E₂) также можно проверить по таблице характеров.

Для характеров неприводимых представлений, как и для матриц, выполняется закон об ортонормированности (2.30), который удобно расписать на два соотношения — отдельно для столбцов (классов C_i ) табл. 2.47 и отдельно для строк (представлений E_α):

где n_i — число элементов в классе C_i, n — порядок группы G, K — число классов C_i, L – число представлений E_α, δ_αβ, δ_ij — символы Кронекера.

Приведем примеры, подтверждающие ортонормированность характеров:

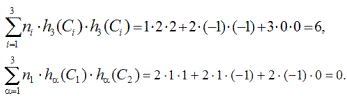
У нас получилось, что K = L. На самом деле, число неприводимых представлений E_α всегда равно числу классов сопряженности C_i. Критерием неприводимости представления E_α служит формула

       (2.34)

Так, представление E₂ является неприводимым, так как

а представление E₄ будет уже приводимым:

Еще одним важным критерием является критерий полноты набора неприводимых представлений, который гласит: сумма квадратов размерностей матриц всех неприводимых представлений должна быть равна порядку группы:

;    D₃: 6 = 1² + 1² + 2².   (2.35)

Разложение (2.35), вообще говоря, неоднозначно. Так, числа 27 и 92 можно разложить на сумму квадратов многими способами:

27 = 1² + 1² + 5² = 1² + 1² + 3² + 4² = 3² + 3² + 3² = 1² + ... + 1² = ...

92 = 1² + 1² + 3² + 9² = 3² + 3² + 3² + 4² + 7² = 1² + ... + 1² + 2² = ...

Критерий неприводимости представлений свидетельствуют о существовании определенной связи между классами эквивалентности C_i и неприводимыми представлениями E_α. Каждому классу можно поставить в соответствие определенное представление. Для группы D₃ это соответствие выглядит следующим образом:

E₀ ↔ C₀, E₁ ↔ C₂, E₂ ↔ C₁.