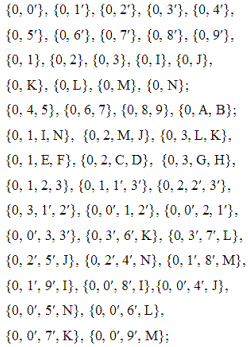Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.3. Групповые решетки из подгрупп

Группа вращения декартовых координат и ее подгруппы

У нас появился прекрасный повод для изучения O_d — этой важнейшей группы симметрии (хотя кое-что о ней было сказано раньше). В табл. 2.65 приведены подстановки S[], составленные по нижнему уровню решетки.

Таблица 2.65

Табл. 2.65 для группы S[] связана с табл. 2.54 для группы вращения куба (или октаэдра) следующим образом: если пронумерованные грани куба (рис. 2.10) обозначить буквами по следующей схеме : 0 → R, 1 → S, 2 → Z, 3 → U, 4 → O, 5 → T, то первые 24 подстановки (с 0 по N) табл. 2.65 совпадут с 24 подстановками столбца O(6) табл. 2.54.

Группа O_d является одновременно группой симметрии декартовых координат. В табл. 2.66 показано соответствие между нашими подстановками и матрицами, преобразующими всеми возможными способами оси координат x, y, z.

Таблица 2.66

Табл. 2.66 составить несложно, если помнить, что матрицы одного класса должны иметь один и тот же характер; подстановки на транспозициях соответствуют симметричным матрицам; обратные подстановки отвечают транспонированным матрицам. В виду важности группы O_d , перечислим все ее подгруппы. При это мы ставим перед собой цель напомнить два простых приема, позволяющих по нескольким известным подгруппам найти большое число неизвестных. Дело в том, что, когда группа небольшого порядка, то все ее подгруппы отыскать несложно. Но наша группа 48-го порядка содержит 84 подгруппы и отыскать их только на основе знания определения группы довольно тяжело.

Самый эффективный способ поиска неинвариантных подгрупп состоит в сопряжении одной какой-то известной подгруппы. Предположим, нам удалось отыскать одну из подгрупп 4-го порядка, не являющуюся нормальным делителем, — {0, 2', 4', N}. Тогда с помощью элемента K и D и с использованием приема поиска сопряженных подгрупп 6-го порядка для голоморфа H(D₃), найдем группы {0, 1', 8', M} и {0, 3', 7', L}. Подробно: из табл. 2.65 находим подстановки

K= (RZ)(SO)(UT) и D = (ZTOU),

тогда 0 → 0 и далее автоматически:

Второй способ, наоборот, связан с нормальными делителями, и он нам тоже, в основном, известен: аналогичным образом мы искали систему гомоморфных проекций для голоморфа H(D₃)/N₁ и т.д. Несложно определить нормальный делитель группы S[] » O_d второго порядка {0, 0'}. Далее, ищем все классы смежности по этому делителю, т.е. систему гомоморфных проекций:

Затем, по известным группам 2-го порядка (их количество определяется числом подстановок на транспозициях, которые берутся из табл. 2.65), ищем группы 4-го порядка по схеме:

{0, 1} → {0, 0', 1, 2'}, {0, 2} → {0, 0', 2, 1'}... {0, N} → {0, 0', 5', N}.

По известным подгруппам 3-го порядка находим неизвестные подгруппы 6-го порядка или по подгруппам 4-го порядка ищем подгруппы 8-го порядка и т.д.:

{0, 8, 9} → {0, 8, 9, 0', I', J'}, {0, 3, L, K} → {0, 3, K, L, 0', 3', 6', 7'}, ...

Таким же образом находим смежные классы по другим инвариантным подгруппам, в частности, по нормальному делителю {0, 1, 2, 3} найдем все 12 проекций:

По известным подгруппам 2-го порядка найдем подгруппы 8-го порядка:

{0, 0'} → {0, 1, 2, 3, 0', 1', 2', 3'}, {0, I} → {0, 1, 2, 3, C, D, I, M}, ...

Комбинируя оба изложенных способа, находим все 84 подгруппы полной группы симметрии куба O_d :

Итак, нами были рассмотрены все 14 групп 16-го порядка. Осталось сделать последний небольшой шаг — составить из них метарешетку M₁₆. Несложный анализ графических изображений всех 14 решеток дает результат, который представлен на рис. 2.26 (числа, стоящие рядом с обозначениями решеток, указывают количество узлов на уровнях).

Рис. 2.26