Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.3. Групповые решетки из подгрупп

Решетки групп 18-го и 20-го порядков

Не останавливаясь на достигнутом, пойдем дальше. За простой циклической группой C₁₇ идут пять групп 18-го порядка. Как выглядит их метарешетка M₁₈? Анализ проведем по сокращенной программе, без поиска групп симметрии решеток. Верхнеполюсной является решетка, построенная от группы, которую обозначим, как . Ее образующими являются:

a = (012)(345),     b = (02)(35),    c = (12)(34).

Тогда главными определяющими соотношениями будут:

ab = ba² = (01)(34),    ac = ca² = (02)(45), 

bcb = cbc = (01)(45),     a²b = ba = (12)(45), 

a²c = ca = (01)(35),     abcb = bcba² = (12)(35).

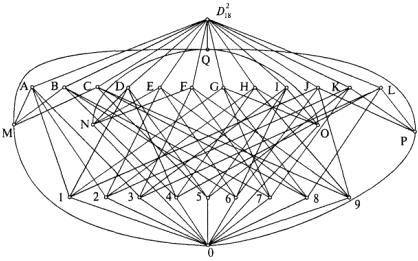
Решетка S() изображена на рис. 2.27.

Рис. 2.27

Подгруппы :

Группу C₃D₃ можно получить либо на трех образующих

a = (012),     b = (02),     c = (345),

либо на двух:

a = (012345),     b = (024).

Решетка S(C₃D₃) сохраняет от решетки S() следующие узлы:

{1, 2, 3, A, D, E, F, M, N, P, O, Q}.

Решетка от группы диэдра S() образована узлами

{1, 2, 3, 4, 5, 6, 7, 8, 9, D, E, F, N, Q},

а две инверсных решетки S(C₃C₆) и S(C₂C₉) — соответственно, узлами

{5, C, D, I, K, M, N, O, P, Q} и {5, D, N, Q}.

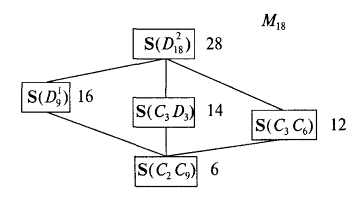
Последняя решетка является нижнеполюсной (C₂C₉ » C₁₈). Метарешетка M₁₈ изображена на рис. 2.28.

Рис. 2.28

Аналогичная метарешетка получается на решетках от групп 20-го порядка (рис. 2.29).

Рис. 2.29

Число рядом с обозначениями решеток указывает на количество узлов на уровнях. Верхним полюсом M₂₀ является решетка S() (рис. 2.30).

Рис. 2.30

Существуют две неинверстные:

S() = {6, C, D, E, F, G, H, K},

S() = {1, 3, 5, 8, A, C, D, E, F, G, H, I},

и две инверсные решетки:

S(C₂C₁₀) = {1, 2, 6, C, H, I, J, K},

S(C₄C₅) = {6, C, H, K}.

Следует также напомнить, что для групп 20-го порядка имеют место изоморфизмы (табл. 2.28):

C₂C₁₀ » C₅,     C₄C₅ » C₂₀,     C₂ » .