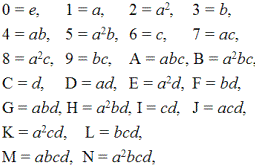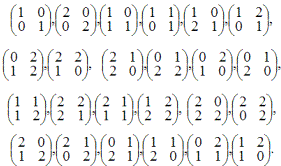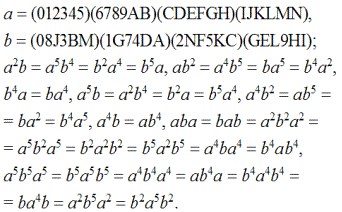Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.3. Групповые решетки из подгрупп

Решетки групп 24-го порядка

По понятным причинам пропускаем группы 21-го, 22-го, 23-го порядков и переходим к анализу групп 24-го порядка. Верхним полюсом метарешетки M₂₄ из 12 правильных решеток является C₂ » D₃ с образующими:

a = (012),     b = (02),     c = (34),     d = (56). 

Если элементы группы D₃ обозначить через:

то подгруппы для построения решетки S(D₃) будут такими:

Нет смысла анализировать многие решетки от групп 24-го порядка, так как их геометрия вполне понятна. Например, решетка S() является простым расширением решетки S(). В самом деле, следующие 15 подгрупп образуют решетку S() (рис. 2.18):

Таким образом, S() является верхней частью решетки S(), и вообще S(D₃) Ì S() Ì S() Ì ... Далее опишем новую для нас (с точки зрения определяющих соотношений) группу с образующими a и b, для которой выпишем все подгруппы для построения решетки S():

Весьма своеобразной является группа с образующими a, b и с нижеслудующими определяющими соотношениями:

Группу можно представить матрицами 2 · 2 с элементами по mod (3):

Если считать матрицы

и т.д. недопустимыми, то общее число допустимых матриц рассматриваемого типа равно 48 и они образуют группу. Эта группа не изоморфна полной группе куба O_d, хотя бы потому, что является у нее нормальным делителем (как известно, у группы O_d нет подгрупп ). Решетка S() содержит всего 8 узлов, так как имеет по одной подгруппе 2-го, 3-го, 4-го, 6-го и 12-го порядка и три подгруппы 8-го порядка. Остальные решетки, входящие в метарешетку M₂₄, ничего примечательного не представляют.

Таблица 2.67

В табл. 2.67 содержится информация об узлах и связях как правильных, так и неправильных решеток от групп 24-го порядка. В заголовке табл. 2.67 решеткам присвоены следующие позиции:

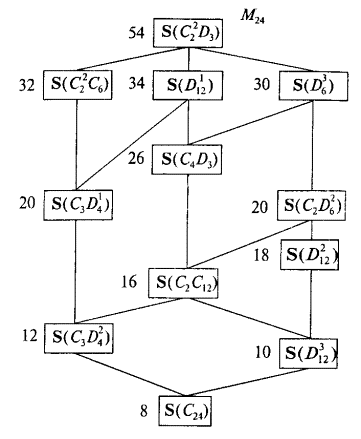
Все связи условно поделены на «отходящие» (идущие от узла вверх) и «приходящие» (подходящие к узлу снизу). Если в ячейке стоит два числа, например 2, 4; это значит, что от одной части узлов отходит 2 связи, а от другой — 4 связи. Общее количество узлов дается без учета полюсов. На рис. 2.31 приведено графическое изображение метарешетки M₂₄, которое показывает иерархию всех 12 правильных решеток, построенных на базе групп 24-го порядка.

Рис. 2.31

Анализ неправильных решеток начнем структурой подгрупп группы T₆, которая самым очевидным образом связана со структурой группы тетраэдра T₃ = T. Образующими элементами для T₆ являются a, b и с нижеслудующими определяющими соотношениями:

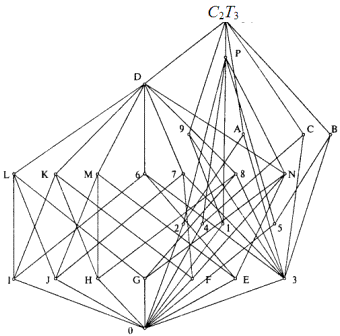
Решетка S(T₆) изображена на рис. 2.32. Ее структура является надрешеткой S(T₃) (рис. 2.20) и одновременно подрешеткой S(C₂T₃), которая изображена на рис. 2.33.

Рис. 2.32

Рис. 2.33

Выпишем подгруппы T₆ и C₂T₃, используя общие символы для соответствующих узлов; для T₆ имеем:

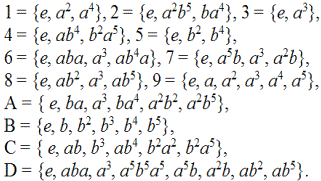
Если решетки S(C₂T₃) и S(T₆) являются верхним и нижним полюсами одной метарешетки, то третья неправильная решетка S(T_d) никак не связана с другими решетками от групп 24-го порядка. Ее 28 подгрупп приведены в списке 84 подгрупп для групп O_d (там необходимо выбрать те подмножества, куда не входят штрихованные символы).

Интересен и сравнительный анализ структур. Например, три решетки от коммутативных групп 40-го порядка —

C₄₀ » C₅C₈,    C₂C₂₀ » C₄C₁₀ » C₂C₄C₅,     C₁₀ » C₅,

с графической точки зрения полностью совпадают с решетками от групп C₂₄, C₂C₁₂ и C₆. Очень схожи решетки S(D₃) и S(D₅) (несмотря на то, что первая насчитывает 52 узла, а вторая — 74), S(C₂) и S(C₂) (число узлов, соответственно, 18 и 26), S(C₄D₃) и S(C₄) (24 и 34) и т.д. Хотя для правильной решетки S(C₂) от группы 40-го порядка уже нельзя найти аналога среди решеток от групп 24-го порядка.

Мы знаем, сколь важную роль играют делители чисел. Схожесть разложений двух чисел:

24 = 2 · 2 · 2 · 3,      40 = 2 · 2 · 2 · 5

обеспечивает и определенную схожесть в структурах для групп соответствующих порядков. Однако здесь нужно иметь в виду следующее обстоятельство. При последовательном возведении в степень подстановки a, представляющей собой 12-цикл, возникает еще три подстановки аналогичной периодичности — a¹¹, a⁷ и a⁵. Отсюда можно пытаться найти три группы 24-го порядка с определяющими соотношениями: ab = ba¹¹, ab = ba⁷, ab = ba⁵. Но для подстановок a, представляющей собой 20-цикл, существует уже семь таких композиций:

ab = ba¹⁹, ab = ba¹⁷, ab = ba¹³, ab = ba¹¹, ab = ba⁹, ab = ba⁷, ab = ba³.

Таким образом, число групп 40-го порядка будет заметно больше, чем групп 24-го порядка. Тем не менее, сравнительный анализ дает многое в понимании строения групп.