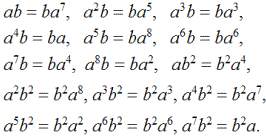Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.3. Групповые решетки из подгрупп

Решетки групп 27-го порядка

Свой морфологический анализ мы закончим группами 27-го порядка (27 = 3 · 3 · 3) с тем, чтобы можно было решетки от этих групп сравнить с решетками от групп 8-го порядка (8 = 2 · 2 · 2). Подгруппы верхнеполюсной группы :

Рис. 2.34

Решетка S(), изображенная на рис. 2.34, обладает простой группой симметрии S[], которая разбивается на восемь классов сопряженности. Общее число элементов в группе равно 5928. По одному представителю от каждого класса и количество элементов в классе отражено в табл. 2.68.

Таблица 2.68

Представители могут играть роль образующих элементов группы. Для группы S[] имеется 13 подгрупп 3-го порядка и такое же число подгрупп 9-го порядка, причем подгруппы четырежды связаны между собой отношением порядка, т.е. каждый узел решетки имеет четыре связи. Несложно подсчитать, что решетка S() будет содержать 31 узел на одном уровне и на каждый узел будет приходиться уже 6 связей; далее, решетка S() имеет 57 узлов на уровне и 8 связей на узел и т.д. Отсюда можно вывести две простых формулы для подсчета числа связей (M) и числа узлов (N) верхнеполюсных решеток S() (p — простое число):

M = p + 1,     N = 3 · p + (p – 1)².

Если взять две четные подстановки:

a = (012)(345)(678),     b = (034)(578)(126)

и перемножить всеми возможными способами, мы уже не получим простой группы, но возникшие при этом 27 подстановок заслуживают самого пристального внимания. Дело в том, что получившаяся группа , отдаленно напоминающая группу диэдра = D₃, обладает замечательным свойством — все ее подстановки представляют собой 3-циклы. Группа распадается на одиннадцать классов сопряженности и имеет следующие подгруппы, обозначенные в соответствии с узлами S()

Группу можно воспроизвести на треугольных матрицах размером 3 · 3 с элементами, взятыми по mod (3):

Эти матрицы образуют нормальный делитель в группе 216-го порядка, состоящей из подобных треугольных матриц, у которых на главной диагонали 8 способами расположены элементы 1 и 2. Решетка S() показана на рис. 2.35.

Рис. 2.35

Следующую некоммутативную группу , как и группу , можно отнести в разряд особых, так как ее решетка S() в точности совпадает с инверсной решеткой S(C₂C₉) от коммутативной группы. Две регулярные подстановки:

a = (012345678)(9DHCGBFAE)(IPNLQOMK),

b = (09I)(1AJ)(2BK)(3CL)(4DM)(5EN)(6FO)(7GP)(8HQ)

могут играть роль образующих, при этом выполняются следующие равенства —

Если подгруппы группы обозначить соответствующим образом:

то с помощью инверсной подстановки i = (1J)(2L)(3O)(7G) можно убедиться (рис. 2.38), что решетка S() окажется действительно инверсной. Но точно такие же подгруппы (причем здесь не нужно менять элементы) получаются для коммутативной группы C₂C₉, если в качестве образующих взять подстановки a = (012345678), b = (9AB). Решетки S(), S(), S() » S(C₂C₉) и S(C₂₇) образуют метарешетку M₂₇, цепь которой, в отличие от M₈ (рис. 2.17), состоит из четырех звеньев.