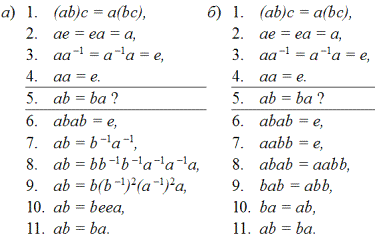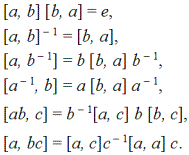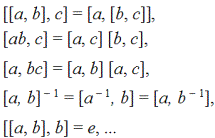Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Какие бывают алгебраические системы

Группы являются краеугольным камнем общей, или абстрактной, алгебры. «Общей», или «абстрактной», алгебра называется потому, что ее объектами являются уже не конкретные «представления» (матрицы или подстановки), а абстрактные символы, для которых заранее вводятся определенные аксиомами операции. Не надо думать, что абстрактные символы к нам «падают с неба», их существование должно быть обеспечено наличием соответствующего представления. Если такового не находится, то убежденный конструктивист, ориентированный на содержательную математику ко всяким манипуляциям с «пустыми» знаками должен отнестись с настороженностью. Если нам говорят, что

(a + b)² = a² + 2ab + b²,

мы доверяем этому равенству в силу существования бесконечного множества конкретных равенств:

(2 + 3)² = 2² + 2 · 2 · 3 + 3² = 25,

(1 + 4)² = 1² + 2 · 1 · 4 + 4² = 25, ...

Примеры с числами обуславливают действия с буквами, но никак не наоборот.

Абстрактная запись дает определенные преимущества. Так, например, вместо индуктивного поиска выражения для разложения кубического бинома, мы могли бы воспользоваться общей формой записи чисел посредством букв, тем более что, с точки зрения письма, нет никакой разницы между символами, скажем, a и 2, b и 3. Если взять значения a = 2, b = 3, затем a = 1, b = 4 и т.д., то вероятность, что при a = 73, b = 152, произойдет сбой и общая формула разложения квадратичного бинома окажется неверной, маловероятно. С одной стороны, чтобы верить в сбой формулы при каком-то числовом значении буквы, нужно верить в чудеса, в сверхъестественную силу, которая бы нарушила монотонность числового ряда. С другой стороны, человек, отрицающий преимущества абстрактной (равно общей, алгебраической) записи, поступает неразумно. Античный математик Диофант, живший в III столетии в Александрии, сначала тоже использовал только цифры, но потом его числовые выкладки разрослись настолько, что он просто вынужден был прибегнуть к буквам. Эта его невинная уловка позволила нынешним историкам математики присвоить ему почетное звание первого алгебраиста мира. Однако трудно поверить, что где-нибудь в Древнем Египте или Вавилоне кто-нибудь из математиков уже не сделал то же самое: этот естественный прием придет каждому в голову, когда дело имеешь с большими числами. 

Для получения принципиально новых знаний буквенная запись дает крайне мало. Она практически не способна выполнять функцию лопаты для откапывания истин. Единственное ее неоспоримое достоинство: убеждать путем алгебраических выкладок в справедливости уже обнаруженных математических соотношений. Продемонстрируем это на следующем примере. Известно, что группа коммутативна (ab = ba) и для любого ее элемента выполняется равенство: a² = e. Этот тривиальный факт, вытекает мгновенно, стоит нам мельком бросить взгляд на подстановки:

e = (0), a = (01), b = (23), c = (45), ab = (01)(23),

ac = (01)(45), bc = (23)(45), abc = (01)(23)(45).

И мы прекрасно знаем, что обратное утверждение ошибочно, т.е. из коммутативности группы ab = ba вовсе не вытекает равенство a² = e для любого элемента a. В этом мы убедились при рассмотрении самых элементарных групп, в частности, C₂C₄:

e = (0), a = (0123), a²= (02)(13), a³= (0321), b = (45),

ab = (0123)(45), a²b = (02)(13)(45), a³b = (0321)(45).

Что же делает убежденный «формалист»? Он берется доказать, что для каждой группы, для которой имеет место равенство a² = e, будет выполняться коммутативный закон: ab = ba. Исходя из условий, абстрактно определяющих группу, он может провести свое доказательство, по крайней мере, двумя способами — (а) и (б):

После этих выкладок можно попросить «формалиста» столь же ловко доказать обратное, а именно, что из условия коммутативности ab = ba вытекает равенство a² = e. У конструктивистов есть пример коммутативной группы C₂C₄, показывающий, что a² ≠ e. Но как обязан поступить последовательный «формалист», у которого этого примера нет перед глазами? Он ведь должен, исходя из аксиом группы и общих алгебраических выкладок, показать возможность или невозможность этого утверждения. Но он никогда не подтвердит и не опровергнет это положение, поскольку для одних групп оно верно, а для других уже нет. Спрашивается, зачем нужно приводить формальные доказательства (а) или (б), если они не обладают достаточной универсальностью?

Между тем, коммутативные группы не представляют собой ничего такого, что может вызвать затруднения. Сложнее обстоит дело с так называемыми нильпотентными группами, для которых справедливо тождество a^m = e, где m > 2. Одну из таких групп мы хорошо знаем, это с образующими:

a = (012)(345)(678),     b = (034)(578)(126),

которая состоит из 27 подстановок, представляющих собой 3-циклы; возведение в куб любого элемента этой группы дает e.

Для нильпотентных групп вводят понятие коммутатора, определяемого следующим образом:

[a, b] = a^–1b^–1ab = aba^–1b^–1.

Коммутатор равен e, если группа коммутативна, в общем же случае он равен некоему другому элементу группы. Так, для группы коммутатор, составленный из a и b, равен: [a, b] = (065)(173)(284). Следовательно, коммутатор можно рассматривать как определенную на группе метаоперацию. Для любых коммутаторов справедливы следующие законы, которые проверяются подстановкой:

Но если группа нильпотентная, то для метаоперации выполняются законы ассоциативности, дистрибутивности и другие замечательные тождества:

Чтобы доказать любое из этих тождеств, конструктивисту не требуется больших интеллектуальных усилий, особенно если у него под рукой компьютер. Нильпотентная группа легко разбивается на одиннадцать классов эквивалентности и прямой подстановкой их представителей устанавливается справедливость любого тождества. Для алгебраиста-формалиста поиск доказательства подобных тождеств выливается в тяжелый и неблагодарный труд; никогда не знаешь, увенчаются ли твои поиски успехом или ты обречен на бесконечное манипулирование символами. Докажем в общем виде, что из равенства a³ = e вытекает равенство [[a, b], b] = e:

Понятно, что данное доказательство формально-символическим образом следует за манипуляциями над конкретными подстановками a и b, полностью опираясь на их 3-циклические свойства. Теперь алгебраистам-формалистам предлагается установить: будет ли из равенства [[a, b], b] = e вытекать равенство a³ = e?

Конечно же, любое из выписанных тождеств для нильпотентных групп с определяющим ее равенством a³ = e прежде устанавливалось индуктивно, на подстановках или выписанных выше матрицах, в частности, для конкретной группы , и лишь затем разрабатывались какие-то общие схемы их доказательства. Искать же «втёмную» правильное решение очень сложно, да и вряд ли необходимо. Число разнообразных групп огромно, а количество «красивых» соотношений между их элементами еще больше.

Сейчас мы хотим познакомить нашего читателя с математическими объектами, тесно связанными с группами. Этими объектами являются поля многочленов, свойство которых сегодня широко используется в процедуре кодирования информации. Чтобы подступиться к конкретным многочленам, нам понадобится ряд новых понятий, в частности, мы вновь вернемся к линейным пространствам, с которых начали главу, чтобы рассмотреть их уже с точки зрения поля. Оговоримся, в этом подразделе любое множество с определенными на нем законами будет называться алгебраической системой, а также просто алгеброй или системой. Группы и поля являются примерами таких алгебраических систем, но они не единственные алгебры, причем мы не станем рассматривать их абстрактно, поскольку это мало поможет в таком практическом деле, как кодирование информации.

Если введена какая-либо операция на множестве, не выводящая элементы за пределы этого множества, то данная алгебраическая система называется группоидом. Если в группоиде существует нейтральный элемент, то система называется квазигруппой (лупой). Если в квазигруппе выполняется закон ассоциативности, то система называется полугруппой (моноидом). Если в полугруппе каждому элементу можно найти обратный, то система называется группой. Если в системе введены одновременно две операции — сложение и умножение, — причем для сложения выполняются все законы коммутативной группы, а по умножению законы группоида и дистрибутивный закон, то система называется кольцом. Если умножение в кольце еще и ассоциативно, то кольцо называется ассоциативным. Если в ассоциативном кольце умножение коммутативно, то система называется ассоциативно-коммутативным кольцом. Если все отличные от нуля элементы кольца составляют группу по умножению, то система называется телом. Если мультипликативная группа, входящая в тело, коммутативна, то система называется полем.

Приведем примеры этих алгебраических систем. Множество всех квадратных матриц образует ассоциативное кольцо. Множество многочленов с действительными коэффициентами от одной переменной с операциями сложения и умножения тоже образуют ассоциативное кольцо. Множество векторов евклидова пространства с операциями сложения векторов и векторного умножения образуют просто кольцо. Множество действительных чисел без нуля по умножению образуют мультипликативную группу. Множество натуральных чисел по сложению образуют аддитивную полугруппу. Множество целых чисел с операциями сложения и умножения образуют поле. Поля образуют и комплексные числа, кватернионы же являются телами. Комплексные числа, кватернионы и числа Клиффорда подчиняются закону ассоциативности, октава ему не подчиняется.

Если в ассоциативной алгебре сохранить аддитивную группу, а операцию умножения заменить метаоперацией симметрирования, т.е. a × b = ab + ba, то будет получено неассоциативное кольцо, в котором для элементов a и b выполняются равенства:

a × b = b × a,     ((a × a) × b) × а = (a × a) × (b × a).

Проверим второе равенство прямой подстановкой, для чего распишем правую часть —

[(aa + aa)b + b(aa + aa)]a + a[(aa + aa)b + b(aa + aa)] =

= aaba + aaba + baaa + baaa + aaab + aaab + abaa + abaa =

= (aa + aa)(ba + ab) + (ba + ab)(aa + aa) = (a × a) × (b × a).

В результате получим левую часть равенства. Эта алгебраическая система носит название кольца Ёрдана. Если в ассоциативной алгебре вместо симметрирования ввести метаоперацию антисимметрирования, т.е. a · b = ab – ba, то будут выполняться два других равенства:

a · b = 0,     (a · b) · c + (b · c) · a + (c · a) · b = 0,

(проверяется аналогично предыдущему случаю). Такая система получила название кольца Ли. Метаоперации симметрирования и антисимметрирования по своей сущности схожи с вышевведенной метаоперацией коммутирования. Кольца Ли и Ёрдана здесь введены абстрактно, как выше были введены нильпотентные группы. Сейчас перейдем к рассмотрению двух конкретных полей, а именно: линейные пространства векторов и пространства двухкомпонентных чисел на базе иррациональности.