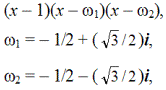Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

2.4. Алгебраические системы на базе групп

Числовые поля

Граница между понятиями числа и вектора, как мы убедились выше, достаточно условна. Тем не менее, зададим два разнородных множества элементов, одно из которых назовем векторами a, b, c, ... ∈ V, другое — числами (скалярами) a, b, c, ... ∈ U. Алгебраическая система называется линейным пространством над полем чисел, если векторы представлены через числа в виде некоторой комбинации базисных векторов e_i :

a = a₁e₁ + a₂e₂ + ... + a_ne_n.

При этом предполагается, что векторы по сложению образуют коммутативную группу, а числа удовлетворяют законам поля; кроме того, выполняются четыре следующих условия —

a(a + b) = aa + ab,         (a + b)a = aa + ba,         (ab)a = a(ba), ea = a.

Говорят, что векторы e_i образуют базис векторного пространства V размерности n. Базис будет считаться линейно независимым, если из равенства

a₁e₁ + a₂e₂ + ... + a_ne_n = 0 следует a₁ + a₂ + ... + a_n = 0.

Векторное пространство V может иметь несколько наборов базисных векторов, поскольку сам базисный вектор e_i может быть выражен через систему векторов, в которой эта базисная составляющая заменена любым другим вектором:

e_i = b₁e₁ + b₂e₂ + ... + b_ia + ... + b_ne_n.

Однако любой набор базисных векторов всегда имеет одинаковое количество базисных компонентов, определяющих размерность пространства V. При нахождении набора базисных векторов или при определении размерности пространств V важно установить, является ли данная совокупность векторов a_i линейно независимой. Это можно сделать несколькими способами, в частности, если система векторов a_i зависимая, то составленный на их основе определитель Грама равен нулю; для трехмерного случая имеем:

γ = = 0.

Если V_i подмножество базисных векторов пространства V, то говорят о подпространстве V_i относительно пространства V. Прямой суммой двух подпространств V₁ и V₂ называется множество векторов вида a_i + b_i, где a_i ∈ V₁, b_i ∈ V₂. Размерность нового пространства N(V₁ + V₂) определяется формулой включения и исключения подмножеств. В нашем случае она выглядит следующим образом:

N(V₁ + V₂) = N(V₁) + N(V₂) + N(V₁ ∩ V₂).

Доопределим линейное пространство V скалярным произведением векторов a и b:

(ab) = a₁b₁ + a₂b₂ + ... + a_nb_n.

В теории кодирования информации дело имеют, как правило, с двоичной системой, так что (ab) = {0, 1}. Если скалярное произведение равно нулю (ab) = 0, то векторы a и b ортогональны. Подпространства V₁ и V₂ будем называть ортогональными дополнениями до пространства V, если каждый вектор из V₁ ортогонален любому вектору из V₂, а прямая сумма подпространств V₁ и V₂ дает целиком пространство V.

Пусть задано линейное пространство V из 16 векторов

a₀ = 0000,         a₁ = 0001,         a₂ = 0010, ... ,         a₁₅ = 1111.

Поставим перед собой задачу выбора системы базисных векторов таким образом, чтобы в нее входили векторы a₇ = 0111 и a₁₄ = 1110. С помощью определителя Грама установим линейную независимость своего базиса, а затем разобьем двумя различными способами пространство V на два ортогональных дополнения.

Размерность нашего пространства равна N(V) = 4. Испытаем четыре вектора a₁, a₄, a₇ и a₁₄ на независимость. С этой целью вычислим соответствующие скалярные произведения:

(a₁a₁) = 0 · 0 + 0 · 0 + 0 · 0 + 1 · 1 = 1,     (a₄a₄) = 1,       (a₇a₁₄) = 0,

(a₁a₄) = 0 · 0 + 0 · 1 + 0 · 0 + 1 · 0 = 0,     (a₄a₁₄) = 1,     (a₁a₇) = 1,

(a₁a₁₄) = 0,     (a₄a₇) = 1,     (a₇a₇) = 1,     (a₁₄a₁₄) = 1.

Определитель Грама отличен от нуля:

γ = = 1.

Следовательно, четыре вектора a₁, a₄, a₇ и a₁₄ могут составить базис, а раз так, то все остальные векторы должны выражаться через них:

Смена базиса привела к перекодированию всех векторов, координаты которых можно представлять некими кодовыми словами. Так, вместо a₁₂ = 1100 появился код 1111, что соответствовало кодовому слову a₁₅, вместо a₁₃ появился код 0111. Ортогональными дополнениями могут быть два векторных подпространства —

V₁ = {a₀, a₁, a₄, a₅} и V₂ = {a₀, a₂, a₈, a₁₀},

поскольку соответствующие скалярные произведения — (a₁a₁₀) = 0, (a₅a₂) = 0 и т.д. — равны нулю. Ортогональными дополнениями будут и пространства

V₁ = {a₀, a₂} и V₂ = {a₀, a₁, a₄, a₅, a₈, a₉, a₁₂, a₁₃};

комбинаций здесь существует множество.

Мы уже говорили, что векторы и матрицы есть некие специфические числа, над которыми можно осуществлять определенные математические действия. Так, традиционные комплексные числа — это двухкомпонентные числа на базе действительной (1) и мнимой (i = √–1) единиц. В роли мнимой единицы может выступать какая-нибудь иррациональная «единица», например, √2 или ∛4. Вообще, иррациональные числа подразделяются на трансцендентные (π, e, lg2, sin5) и алгебраические. Действительное число называют алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами. С этой точки зрения, традиционные комплексные числа тоже будут алгебраическими, так как они являются корнями уравнения n-ой степени.

В практических задачах электротехники рациональное число, например 2,1, часто складывают с иррациональным √3 ≈ 1,7 и получают приблизительный результат 3,8. С точки зрения теории чисел, этого делать нельзя: иррациональные числа, как и комплексные, являются типичными представителями двухкомпонентных векторов. В частности, корнями квадратного уравнения с целыми коэффициентами x² – 6x + 1 = 0 является пара двухкомпонентных чисел

x₁ = 3 + 2√2     и     x₂ = 3 – 2√2.

Общий вид таких чисел — c = a + bi, i = √2 — схож с видом комплексных чисел, только в роли мнимой единицы здесь выступает иррациональное число. Действия над двухкомпонентными числами на базе иррациональности во многом аналогичны действиям над комплексными числами. В частности, формула умножения в обоих случаях выглядит одинаково:

(a₁ + b₁i) (a₂ + b₂i) = (a₁a₂ + b₁b₂i²) + (a₁b₂ + a₂b₁)i.

Кроме того, нормированным комплексным числам удовлетворяет уравнение окружности:

1 = x² + y² = (x + yi) (x – yi),     где x = cos φ, y = sin φ.

Двухкомпонентным числам на базе √2 также можно поставить в соответствие аналогичное уравнение:

1 = x² – 2y² = (x + y√2) (x – y√2).

Решениями этого уравнения служат два числа x₀ = 3, y₀ = 2, но не только. Чтобы найти другие решения этого уравнения, нужно последовательно возводить в степень числа 3 ± 2√2, в частности,  

(3 ± 2√2)² = 17 ± 12√2,  

следовательно, пара чисел x₁ = 17, y₁ = 12 также удовлетворяет уравнению. Следующее решение получается при возведении исходного числа в куб  

(3 ± 2√2)³ = 90 ± 70√2, значит, x₂ = 90, y₂ = 70 и т.д. 

Уравнение вида 1 = x² – Dy² называется уравнением Пелля; ему удовлетворяет бесконечная последовательность пар чисел. Например, если D = 7, т.е. i = √7, то уравнение Пелля, имеющего вид 1 = x² – 7y², выполняется при x₀ = 8, y₀ = 3; x₁ = 127, y₁ = 48 и т.д.; если D = 13, то x₀ = 18, y₀ = 5; x₁ = 649, y₁ = 180 и т.д.

Пусть дано уравнение 2x² + 5x + 4 = 0. В поле действительных чисел оно не имеет решений, но в поле комплексных чисел решение уже есть. Существует оно и в поле вычетов по mod (11). В самом деле,

x_1,2 = mod (11) = {2, 1}.

Данная ситуация схожа с решением кубического уравнения x³ – 1 = 0 в полях действительных и комплексных чисел. В поле действительных чисел он разлагается на два неприводимых множителя — (x – 1)(x² + x + 1), а в поле комплексных чисел его можно представить тремя сомножителями

— кубические корни, образующие группу с умножением по табл. 2.69. В поле двух чисел {0, 1}, т.е. в поле вычетов по mod (2), это кубическое уравнение может быть разложено на три скобки с корнями c₁ = 1, c₂ = x, c₃ = x + 1.

Таблица 2.69

Теперь рассмотрим только такие квадратные уравнения ax² + bx + c = 0, у которых коэффициенты являются всевозможными вычетами по mod (5). Тогда корнями этих уравнений станут числа 0, 1, 2, 3 или 4. Квадраты этих чисел могут дать только три из пяти чисел:

0² = 0,         1² = 1,         2² = 4,         3² = 4,         4² = 1.

Другими словами, среди вычетов по mod (5) нет чисел, квадраты которых равнялись бы 2 или 3, а это значит, что уравнения x² = 2 или x² = 3 не имеют решений. Чтобы эти уравнения все же решались, введем иррациональность √2. Тогда вместо пяти чисел получим поле из 25 чисел:

Не выходя за рамки этого множества, можно производить сложение и умножение чисел. Каждый элемент этой финитной арифметики является той или иной степенью образующего элемента 2 + √2:

(2 + √2)² = 1 + 4√2, ... , (2 + √2)²⁴ = 1 + 0√2.

Можно ввести числа a + b√3 и путем последовательного возведения в степень получить новое поле на базе иррациональности √3, в частности:

(3 + 2√3)² = 1 + 2√3,         (3 + 2√3)³ = 0 + 3√3, ...

Возможно построение поля на базе двух иррациональностей — √2 и √3; в этом случае будем иметь трехкомпонентные числа типа a + b√2 + c√3, взятые по mod (5) и т.д.