Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.1. Группы цепей графа

Задача Гамильтона о цепях додекаэдра

В 1859 г. сэр Вильям Гамильтон, знаменитый ирландский математик, давший миру теорию комплексного числа и кватерниона, предложил детскую головоломку, в которой предлагалось совершить «кругосветное путешествие» по 20 городам, расположенным в различных частях земного шара. Каждый город соединялся дорогами с тремя соседними так, что дорожная сеть образовывала 30 ребер додекаэдра, в вершинах которого находились города a, b ... t (рис. 3.11). Обязательным условием было требование посетить каждый город, за исключением первого, лишь один раз.

Рис. 3.11

Если путешествие начать из города a, то последними должны быть города b, e или h, иначе мы не сможем вернуться в первоначальный пункт a. Непосредственное исчисление показывает, что число таких замкнутых маршрутов равно 60.

Можно потребовать посещения всех городов строго по одному разу, включая и первый, т.е. допускается окончание путешествия в любом городе (например, предполагается, что в начальный пункт можно будет вернуться самолетом). Тогда общее число цепных маршрутов увеличится до 162. В табл. 3.4 перечислены все эти цепи, причем в специально организованной последовательности. Принцип организации цепей для додекаэдра выбран тот же, что и ранее для куба, т.е. принцип инверсии хвостовой последовательности вершин. Однореберная замена касается 1, 4, 7, 10, 13 или 16 ребра каждой цепи. Таким образом, получается 11 циклов по 15 цепей в каждом и 3 цикла по 14 цепей.

Таблица 3.4

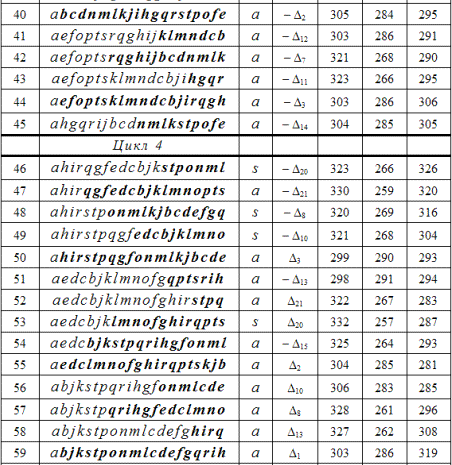
Рассматривая табл. 3.4, можно заметить, что ни один из предложенных дорожных маршрутов не заканчивается в пунктах c, d, f, g, i и j. В пункте t заканчиваются только 6 маршрутов, в пунктах m, p и s — по 8 для каждого пункта, в l, k, n, o, q, r — по 12 и в b, e, h — по 20. Это происходит потому, что для додекаэдра существует пять классов вершин и семь классов ребер, которые в табл. 3.5 количественно разнесены по 11 циклам.

В столбце S табл. 3.4 указана симметрия цепи, которая для додекаэдра определяется так же, как и для куба. Общее число цепей додекаэдра равно произведению 162 × 10 = 1620. Подгруппа G_20a состоит из 162 × 161 + 1 = 26 083 переходов между цепями, привязанными к в вершине a. В группе же G₂₀ насчитывается почти в 100 раз больше переходов.

Гамильтонова задача о путешественнике нередко преобразуется в задачу о коммивояжере. Коммивояжер не праздно путешествующий турист, а деловой человек, ограниченный временными, денежными или какими-либо другими ресурсами. Пусть каждое из ребер снабжено числовой характеристикой: это может быть километраж, время на дорогу или стоимость билета. Таким образом, условные характеристики ребер дадут числовой ряд от 1 до 30, элементы которого могут быть распределены между ребрами додекаэдра как угодно, в частности, в табл. 3.5 дается три варианта распределения реберных характеристик — A, B и C.

Таблица 3.5

Известны алгоритмы поиска маршрута с минимальной суммой реберных характеристик, которые, однако, не учитывают классификацию ребер, а значит и маршрутов, с топологической точки зрения; оптимизация ведется только по метрическим характеристикам ребер. Между тем, табл. 3.5 (столбец N) показывает, что чисто топологический вклад ребер в гамильтоновы маршруты различен. Например, частота появления в гамильтоновой цепи ребра bc на 30 % превышает частоту появления, казалось бы, точно такого же ребра cl. Все ребра в додекаэдре равноправны, если не существует привязки. Но как только появляется привязка (начало путешествия или некий центр управления симметричной системой типа додекаэдра), тотчас появляется неравноправие между связями. Величина этого неравноправия, едва заметная для ребер классов C₃, C₆ и C₇, становится весьма ощутимой для ребер классов C₁, C₂, C₄ и C₅.

Для привязки a существует 27 однореберных замен Δ_i, распадающихся на 6 классов (табл. 3.6). Для Δ_i выполняются равенства:

Таблица 3.6

Реберные разности Δ_i позволяют существенно сократить число операций при нахождении длин, поскольку каждая последующая цепь в цикле отличается от предыдущей на какую-то одну из 27 величин Δ_i. Следовательно, необходимо рассчитать 11 цепей для варианта ΣC, представляющих циклы, и столько же для ΣA; для варианта ΣB длина может быть уже вычислена по формуле:

где числа 190 и 399 отвечают самой короткой и самой длинной цепи, которые только возможны.

Суммы всех длин гамильтоновых цепей по максимальному (ΣΣA), минимальному (ΣΣB) и промежуточному (ΣΣC) вариантам распределения равны следующим величинам:

ΣΣA = 51 939,     ΣΣB = 35 747,     ΣΣC = 46 229,

что составляет весьма заметную разницу между вариантами распределения одних и тех же величин. Отметим также, что максимальная (минимальная) длина в 356 (233) условных единицах приходится на гамильтоновы цепи под номерами 92 и 104. Минимальное значение для промежуточного варианта распределения равно 271 (цепь 37), а максимальное — 345 (цепь 120).