Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
3.3. Кодирование, автоматы и группы на графах
Ликвидация эквивалентных состояний
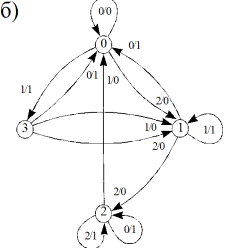
Изучим проблему эквивалентности состояний автоматов под несколько иным углом зрения. На рис. 3.51а изображен автомат A, внешне заметно отличающийся от автомата A', изображенного на рис. 3.51б. Между тем их реакция (y) на входные последовательности из 0, 1 и 2 (x) абсолютно одинакова (табл. 3.29).
Рис. 3.51
Таблица 3.29
x 0 1 2 2 0 1 1 1 2 1 2 0 1 ... y 0 1 0 0 1 0 1 0 0 0 0 1 1 ... q 0 4 3 2 2 0 4 1 2 0 3 0 4 ... q' 0 3 1 2 2 0 3 1 2 0 1 0 3 ... Установить причину такого поведения автоматов помогут таблицы переходов и выходов для A (табл. 3.30) и для A' (табл. 3.31). Из табл. 3.30 видно, что состояния 1 и 3 для автомата A одинаковы. Поэтому строку, отвечающую состоянию 3, из этой таблицы можно просто вычеркнуть, а цифры 3 и 4 заменить на 1 и 3, соответственно. Тогда табл. 3.30 переходит в табл. 3.31, которая представляет переходы и выходы как будто бы совершенно другого автомата A'.
Таблица 3.30
q/x 0 1 2 0 0,0 4,1 3,0 1 0,1 1,1 2,0 2 2,1 0,0 2,1 3 0,1 1,1 2,0 4 0,1 1,0 3,0 Таблица 3.31
q/x 0 1 2 0 0,0 3,1 1,0 1 0,1 1,1 2,0 2 2,1 0,0 2,1 3 0,1 1,0 1,0 Рассмотрим более сложную ситуацию. Табл. 3.32 задает функции переходов и выходов автомата, принимающего десять различных состояний. Все строки таблицы различны, однако может случиться так, что некоторые из состояний окажутся эквивалентными. Тогда при одинаковом обозначении эквивалентных состояний в таблице появятся и одинаковые строки. Остается только выяснить, какие именно состояния эквивалентны. Разобьем все состояния на предварительные классы эквивалентности (Ci), исходя из одинаковости выходных символов (классы Ci проставлены в последнем столбце табл. 3.32). Теперь по отдельности рассмотрим каждый из классов. Для этого пять строк класса C0 оформим табл. 3.33, в которой вместо выходного символа указан класс эквивалентности состояния.
Таблица 3.32
q/x 0 1 2 Ci 0 1,1 0,1 1,0 C0 1 5,0 3,1 8,1 C1 2 1,0 6,0 9,1 C2 3 9,1 6,1 4,0 C0 4 7,0 3,0 9,1 C2 5 7,0 8,0 3,1 C2 6 3,1 9,1 2,0 C0 7 5,0 6,1 8,1 C1 8 8,1 0,1 2,0 C0 9 6,1 3,1 4,0 C0 Таблица 3.33
q/x 0 1 2 Ci 0 1,C1 0,C0 1,C1 C0 3 9,C0 6,C0 4,C2 C3 6 3,C0 9,C0 2,C2 C3 8 8,C0 0,C0 2,C2 C3 9 6,C0 3,C0 4,C2 C3 Таблица 3.34
q/x 0 1 2 Ci 3 9,C3 6,C3 4,C2 C3 6 3,C3 9,C3 2,C2 C3 8 8,C3 0,C0 2,C2 C4 9 6,C3 3,C3 4,C2 C3 Таблица 3.35
q/x 0 1 2 Ci 3 9,C3 6,C3 4,C2 C3 6 3,C3 9,C3 2,C2 C3 9 6,C3 3,C3 4,C2 C3 Таблица 3.36
q/x 0 1 2 Ci 1 5,C2 3,C3 8,C4 C1 7 5,C2 6,C3 8,C4 C1 Таблица 3.37
q/x 0 1 2 Ci 2 1,C1 6,C3 9,C3 C2 4 7,C1 3,C3 9,C3 C2 5 7,C1 8,C4 3,C3 C2 Таким образом, окончательно десять исходных состояний распались на шесть классов эквивалентности:
C0 = {0}, C1 = {1, 7}, C2 = {2, 4}, C3 = {3, 6, 9}, C4 = {8}, C5 = {5}.
Следовательно, исходная таблица переходов и выходов (табл. 3.32), куда входило десять состояний, может быть сокращена до шести состояний (табл. 3.38), при этом функция автомата по преобразованию входных последовательностей в выходные не меняется. Шесть новых состояний получили свои обозначения от индексов своих классов эквивалентности.
Таблица 3.38
q/x 0 1 2 Ci 0 1,1 0,1 1,0 C0 1 5,0 3,1 4,1 C1 2 1,0 3,0 3,1 C2 3 1,0 4,0 3,1 C3 4 4,1 0,1 2,0 C4 5 1,0 4,0 3,1 C5