Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

3.3. Кодирование, автоматы и группы на графах

Графы кватерниона и тетраэдра

При проектировании автоматов могут появиться эквивалентные (лишние) состояния, которые на практике приводят к перерасходу материальных средств. Но зададимся вопросом: какую функциональную нагрузку несет на себе понятие состояние? Ведь автомат-преобразователь, который можно назвать автоматом типа «вход — выход — состояние», просто трансформирует входные сообщения (x_i) в выходные (y_i); участие третьей компоненты — состояние (q_j) — здесь ненужно.

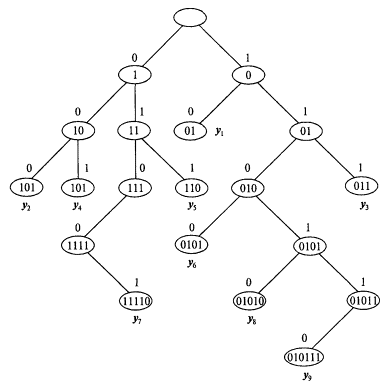
Возможно, что понятие состояния возникло в связи с реализацией автоматов на конкретных устройствах — триггерах, которые могут находиться в одном из двух состояний — 0 или 1. Автомат с большим числом состояний имеет множество триггеров и их состояния тесным образом увязаны с поступающими на вход и снимаемыми с выхода сигналами. Но вне проблем реализации это понятие излишне. Автомат A считается аналитически заданным, если задан список сообщений: y_i = A(x_i). При графическом же отображении автомата типа «вход — выход» должны фигурировать только входные и выходные символы. Договоримся, у дуг писать входные символы, в узлах — выходные, начальное состояние оставим "пустым". Тогда списку из девяти слов будет отвечать бинарное дерево (рис. 3.52), напоминающее бинарные деревья, которые мы строили для кодов Фано (рис. 3.35) и Хаффмана (рис. 3.36). Деревья же Фано и Хаффмана по сути являются автоматами типа «вход».

Рис. 3.52

Основным свойством группы, как известно, является замкнутость. Автомат «вход — выход», представляющий группу, является сильно связанным орграфом. Табл. 3.39, как часть таблицы перемножения элементов кватерниона (табл. 2.23), является таблицей автомата «вход — выход». В качестве входных сообщений здесь выбраны образующие a и b, а в роли выходных выступают все восемь элементов кватерниона, включая образующие.

Таблица 3.39

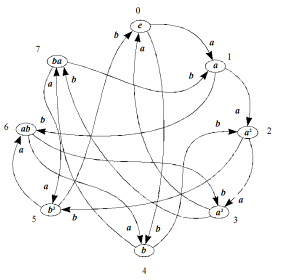
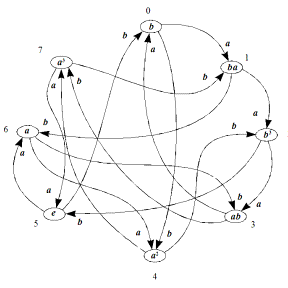
q/x	a	b
e	a	b
a	a2	ab
a2	a3	b3
a3	e	ba
b	ba	a2
b3	ab	e
ab	b	a3
ba	b3	a

Табл. 3.39 определяет симметричную структуру сильно связанного орграфа (рис. 3.53). Поставим на место элемента e элемент b. Тогда дуги орграфа сами укажут новый порядок расстановки остальных элементов (рис. 3.54). Чтобы убедиться в том, что вершины данного орграфа подчиняются группе кватерниона, нужно вместо тождественного элемента e последовательно подставлять все другие элементы группы, не меняя расположения и характеристик дуг. Для удобства написания подстановок все вершины орграфа пронумеруем. После расстановки «выходных сообщений» (рис. 3.54) легко записать соответствующую элементу b подстановку. Если вместо e подставить элемент a, получим подстановку еще одной образующей:

a = (0123)(4657),     b = (0425)(1736).

Рис. 3.53

Рис. 3.54

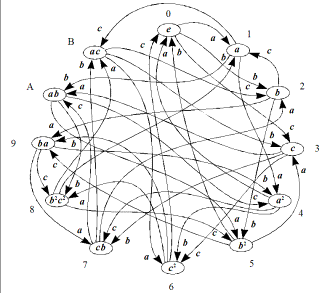
Для каждой группы подстановок можно вычертить свой сильно связанный орграф, который одновременно представляет собой автомат-преобразователь типа «вход — выход». Трудно придумать более наглядную форму графического изображения группы, демонстрирующую ее природу замкнутости. Действительно, разве есть что-нибудь общего между орграфом, изображенным на рис. 3.55, и изображением тетраэдра или решетки его подгрупп?

Та легкость, с которой получаются регулярные подстановки группы тетраэдра T, записанные с помощью орграфа (рис. 3.55), ставят автоматное представление группы T вне конкуренции с ее геометрическим и решетчатым представлениями. Выпишем регулярные подстановки трех образующих группы тетраэдра T :

a = (014)(2A6)(3B7)(589),
b = (025)(193)(47A)(6B8),
c = (036)(1A8)(279)(45B).

Табл. 3.40 является таблицей «вход — выход» для автомата, представляющего группу тетраэдра с тремя «входными сообщениями». Однако мы хорошо помним, что группу T можно получить и с помощью двух образующих — a, b. Следовательно, существует иная таблица «вход — выход» (табл. 3.41), которой будет отвечать и несколько другой орграф. В последнем случае из каждой вершины будут выходить (и соответственно, входить) не по три, а только по две дуги. Такой орграф можно получить из того, что изображено на рис. 3.55 путем удаления всех дуг с входной характеристикой c.

Таблица 3.40

#	(ij...)	q/x	a	b	c
0	(0)	e	a	b	c
1	(012)	a	a2	ab	ac
2	(123)	b	ba	b2	a
3	(013)	c	ab	cb	c2
4	(021)	a2	e	c2	cb
5	(132)	b2	c	e	ba
6	(031)	c2	b2c2	ba	e
7	(023)	cb	b	ac	ab
8	(032)	b2c2	ac	a	b2
9	(01)(23)	ba	cb	a2	b2c2
A	(02)(13)	ab	b2	b2c2	a2
B	(03)(12)	ac	c2	c	b

Таблица 3.41

#	(ij...)	q/x	a	b
0	(0)	e	a	b
1	(012)	a	a2	ab
2	(123)	b	ba	b2
3	(013)	b2a	ab	ba2
4	(021)	a2	e	a2b
5	(132)	b2	b2a	e
6	(031)	a2b	ab2	ba
7	(023)	ba2	b	ab2a
8	(032)	ab2	ab2a	a
9	(01)(23)	ba	ba2	a2
A	(02)(13)	ab	b2	ab2
B	(03)(12)	ab2a	a2b	b2a

Рис. 3.55

Мы также знаем, что для любой группы по числу образующих имеется нижняя граница, но нет верхней, т.е. количество образующих для кватерниона может быть равно восьми, а для тетраэдра — двенадцати. Отсюда автоматные представления кватерниона (рис. 3.53) и тетраэдра (рис. 3.55) далеко не единственны. Вместо регулярного орграфа группу может представлять полный орграф.