Дискретная математика:
логика, группы, графы, фракталыАкимов О.Е.
3.4. Лингвистические и поисковые графы
Порождающая грамматика
Казалось бы, трудно найти более благодатную почву для применения теории графов на практике, чем лингвистика. Генерация предложений из слов и генерация слов из букв — процесс в меру случайный и закономерный. Трансляция текстов с одного языка на другой — вещь крайне необходимая. Сегодня существует масса компьютерных переводчиков, которые работают по алгоритму, а значит, в основе их лежит некая логическая схема, имеющая непременно графическое представление древовидной формы. Чем не задача по кодированию? Однако разработчики этих трансляторов сталкиваются с непреодолимыми препятствиями. Чтобы их понять, нужно вникнуть в существо языковых проблем.
Возьмем простое предложение:
Маленький мальчик играет в мяч.
Если воспользоваться компьютерным переводчиком Stylus v. 2.5, то получим следующий английский эквивалент:
The small boy plays in a ball.
Но обратный перевод с использованием Stylus по смыслу даст несколько другую фразу:
Маленький мальчик играет в шаре.
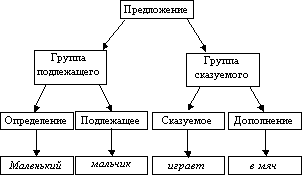
Обратимся к формальной стороне дела. Исходную фразу можно представить порождающим деревом (рис. 3.56). Ситуация напоминает ту, с которой мы имели дело в разделе «Логика» (п. 2.10), где составляли ПРОЛОГ-программы. В нашем случае можно обойтись без предикатов, а также вместо записи y ⇐ x использовать x ⇒ y, которая читается более естественно: « x заменить на y ». Программа, отвечающая этому порождающему дереву, будет выглядеть следующим образом:
1) предложение ⇒ группа подлежащего, группа сказуемого.
2) группа подлежащего ⇒ определение, подлежащее.
3) группа сказуемого ⇒ сказуемое, дополнение.
4) дополнение ⇒ в мяч.
5) дополнение ⇒ в шаре.
6) сказуемое ⇒ играет.
7) подлежащее ⇒ мальчик.
8) подлежащее ⇒ мальчишка.
9) определение ⇒ маленький.
10) определение ⇒крохотный.
11) определение ⇒ низкий.
Рис. 3.56
Система приоритетов Stylus устроена так, что из предложенного набора синонимов были выбраны слова под номерами 5, 7 и 9, вместо 4, 7 и 9; существовали и другие варианты.
Теперь, обобщив приведенный пример, дадим формальное определение языка и порождающей грамматики. Языком L(G), сформированным под воздействием порождающей грамматики G, называется множество предметных слов V, выведенных из корня S с использованием правил P. Порождающей грамматикой G называется семейство четырех множеств:
G = {S, V, W, P},
где S — начальное или корневое слово, причем S берется из W; V — основной или предметный словарь; W — вспомогательный или синтаксический словарь; P — список логических правил вывода или подстановок.
В предыдущем примере имели:
S = предложение;
V = {крохотный, маленький, низкий, мальчик, мальчишка, играет, в шаре, в мяч};
W = {предложение, группа подлежащего, группа сказуемого, подлежащее, сказуемое, определение, дополнение};
P = { 1) предложение ⇒ группа подлежащего, группа сказуемого. ... 11) определение ⇒ низкий}.
Если убрать запятые между синтаксическими словами и ввести их в качестве разделителя между правилами, то вышеприведенная программа будет иметь вид:
1) S ⇒ AB, 2) A ⇒ CD, 3) B ⇒ EF, 4) F ⇒ a, 5) F ⇒ b, 6) E ⇒ c, 7) D ⇒ d, 8) D ⇒ e, 9) C ⇒ f, 10) C ⇒ g, 11) C ⇒ h.
При этом были введены для синтаксических слов большие латинские буквы, а для предметных — малые. Язык примера ограничен двенадцатью предложениями, которые продиктованы порождающим автоматом типа «правило — выход». Граф этого автомата представляет собой дерево. Не станем вычерчивать его целиком, а приведем лишь две ветви, одна из которых отвечает возможному ходу вывода предложения «Маленький мальчик играет в мяч» (рис. 3.57а), другая — «Маленький мальчик играет в шаре» (рис. 3.57б).

Рис. 3.57
Никаких входных слов здесь нет, но есть выходные предложения и правила их вывода. Дуги автомата снабжены номерами, отвечающими порождающим правилам. Каждая дуга играет роль имплицитной логической связки « ⇒ », с помощью которой осуществляется вставка нужного слова. Дерево порождающего автомата — это наиболее приемлемая форма представления процесса формирования грамматических предложений.С помощью автомата «правило — выход» можно генерировать кодовые слова. Грейбах предложил восемь правил для вывода всевозможных кодовых слов с одинаковым числом символов 0 и 1:
1) S ⇒ 0B, 3) A ⇒ 0, 5) A ⇒ 1AA, 7) A ⇒ 0S, 2) S ⇒ 1A, 4) B ⇒ 1, 6) B ⇒ 0BB, 8) B ⇒ 1S.
Здесь по-прежнему большие латинские буквы обозначают вспомогательные переменные, а числа 0 и 1 являются предметными символами. На рис. 3.58 показан вывод двух слов — 011100 и 1001. Эти примеры еще раз говорят в пользу того, что граф, подобно тени, следует за объективным процессом, который он представляет. Стоит процедуре словообразования измениться, и прежние графические формы, столь хорошо иллюстрирующие взаимосвязь отдельных фаз, отказываются работать.

Рис. 3.58
Всякий граф есть автомат для получения каких-то выходных сообщений по заданным параметрам. В зависимости от этих исходных параметров нужно выбирать и тип автомата. Если параметрами для выходных сообщений служат только входные символы (например, кодирование по Фано и Хаффману), удобно использовать граф-автомат, типа «вход». Если каждый входной символ преобразуется в определенный выходной, можно использовать граф-автомат типа «вход — выход» или «вход — выход — состояние». Наконец, если в роли входного слова (символа) выступает одно корневое, из которого затем по заданным правилам порождаются выходные предложения (слова), тогда эффективнее всего использовать граф-автомат типа «правило — выход».
Мы убедились, что генератор кодовых слов Грейбаха действует точно и однозначно. К сожалению, для разработчиков компьютерных программ и к счастью для литераторов, в естественных языках господствует полная свобода выбора, если не сказать, произвол со стороны лингвистического субъекта. Словообразование обыденного разговорного языка нельзя подчинить каким-то строгим логико-математическим законам и не потому, что мы их не знаем, а потому, что их там просто нет. Составление предложений и отдельных слов — процессы творческие, включающие многие культурно-исторические и эстетические моменты. Задача перевода не является обычной кодировкой; здесь не применимы известные нам критерии оптимальности и помехозащищенности кодового слова от случайного сбоя его в канале связи. Хотя в лингвистике задачу порождения правильных предложений путем присоединения к подлежащему и сказуемому разъясняющих и дополняющих слов или задачу порождения правильных слов путем присоединения к корню слева и справа устойчивых буквенных сочетаний можно и нужно трактовать как деревообразующий процесс.
Разработка программ, производящих минимальный алгоритм поиска наилучшей словесной реализации на лингвистическом дереве, считается одной из приоритетных задач функционального и структурного программирования. Выбор оценочного критерия, который бы «отрубал» ненужные ветви поиска и обеспечивал решение на заданном, не слишком глубоко залегающем лингвистическом уровне, является задачей номер один в программировании. Чтобы отсечь на этом дереве ненужную группу слов или словообразующих элементов, необходимо хорошо представлять природу лингвистических составляющих, понимать, с чем собственно вы имеете дело, когда подбираете слова для выражения той или иной мысли и нужную словоформу для данного грамматического предложения.